初中数学浙教版九年级下册3.3 由三视图描述几何体一等奖课件ppt

这是一份初中数学浙教版九年级下册3.3 由三视图描述几何体一等奖课件ppt，文件包含33由三视图描述几何体课件ppt、33由三视图描述几何体教案doc、33由三视图描述几何体学案doc等3份课件配套教学资源，其中PPT共26页， 欢迎下载使用。
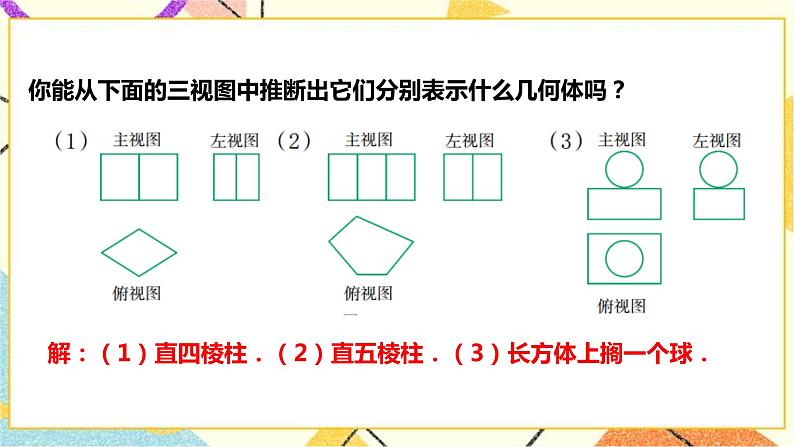
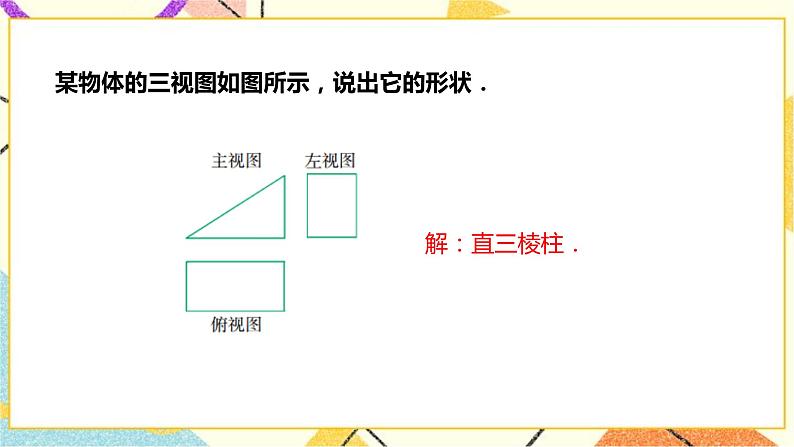
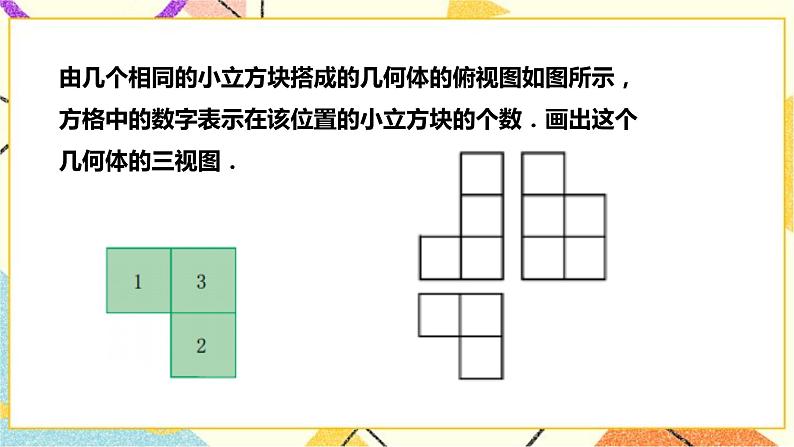
3.3由三视图描述几何体课题 3.3由三视图描述几何体单元第三单元学科数学年级九年级（下）学习目标1．会根据三视图描述简单几何体．2．通过由三视图描述简单几何体， 进一步认识三视图．3．体验三视图在解决表面积计算等实际问题中的应用．重点将三视图转化为立体图． 难点理解三视图转化为立体图的过程． 教学过程教学环节教师活动学生活动设计意图导入新课由于三视图不仅反映了物体的形状，而且反映了各个方向的尺寸大小，设计人员可以把自己构思的创造物用三视图表示出来，再由工人制造出符合各种要求的机器、工具、生活用品等，因此三视图在许多行业有着广泛的应用．根据三视图，工人就能制造出符合设计要求的零件．本节的引入部分使学生知道由三视图描述几何体的实际意义．画三视图和识读三视图是制图学中两大基本内容，教学中可以提供一些工人师傅根据三视图加工零件的实例，最好是机械图纸和相应零件实物．根据三视图说出立体图形的名称         解：（1）直四棱柱．（2）直五棱柱．（3）长方体上搁一个球．根据不同的俯视图画出立体图    •          一般地，三视图中有两个图形是长方形，考虑是柱体____;•          如果第三个图形为 圆，则是 ___圆柱___ ；•          如果第三个图形为 n边形则是 _直n棱柱________；          •          一般地，三视图中有两个图形是三角形，考虑是 锥体•          如果第三个图形为圆则是圆锥； 思考自议对于复杂的物体，由三视图想象出实物体原型，计算时先应搞清三个视图的长、宽、高与实物体的对应关系．    运用空间想象能力由三视图描述几何体．    讲授新课二、提炼概念.对比较复杂的三视图，根据三视图中各线条的结构关系，拆分出一些基本几何体的三视图，想象出相应的几何体再组合成所求的几何体．     三、典例精讲1．已知一个几何体的三视图如图所示，描述该几何体的形状，量出三视图的有关尺寸，并根据已知的比例求出它的侧面积（精确到0.1cm2）．分析：由主视图和左视图知道，这个几何体是直棱柱．但不能确定棱的条数．再由俯视图可以确定它是直四棱柱，且底面是梯形．解：这个几何体是底面为梯形的直四棱柱．量出有关尺寸，根据比例1︰3．可得这个直四棱柱各个方向的尺寸，如图．它的四个侧面都是长为9cm的长方形，前侧面的宽为3cm，后侧面的宽为6cm，左侧面的宽为4.5cm．由勾股定理，可得右侧面的宽为（cm）．所以它的侧面积为3×9＋6×9＋4.5×9＋×9≈170.2（cm2）．答：这个几何体的侧面积为170.2cm2．此范例包含了多种基本技能的训练，具有实际意义，在教学中可以按以下步骤进行 ：（1）根据所提供的三视图，启发学生判断该三视图所表示的几何体的形状，由主视图、左视图可以断定它是哪一类几何体，由俯视图你可以确定什么？从而确定三视图所表示的几何体，是直四棱柱，由于还要求计算该直四棱柱的侧面积，所以最好要能画出立体图，便于尺寸标注，给计算带来方便． （2）从课本量出俯视图的各条边长和主视图的高，这是计算该直四棱柱的侧面积所必需的数据，值得注意的是，从三视图中量出的尺寸数据并不是实际尺寸，还需根据三视图中注明的比例求出实际尺寸，这一点学生容易疏忽，教学中应予以强调，如果已经画出立体图，那么可把实际尺寸数据标注在立体图上，这样比较直观．（3）计算直四棱柱的侧面积，教学时可作如下启发．①直棱柱的各个侧面都是什么图形？有几个？②根据测量所获得的尺寸，可算出哪几个侧面的面积？要算右侧面的面积还缺什么数据？③根据底面是一腰和两底底垂直的梯形（直角梯形），你能算出要侧面的宽吗？如果学生有个困难，可添一条辅助线，将底面分割成一个长方形和一个直角三角形，让学生思考．右侧面矩形的宽当然也可以通过测量得出，但测量容易产生，误差，通常要尽可能少用，直接测量得到的尺寸数据．（4）在回顾小结时，可以帮助学生总结出直四棱柱的侧面积的计算公式：S＝lh（l表示地面周长，h表示高）．本例也可做应适当引申，比如求出这个直四棱柱的全面积，表面积或体积．   三视图与物体的表面展开图往往结合在一起，一般可先由三视图想象出几何体，再画出几何体的表面展开图进行有关计算．         对比较复杂的三视图，根据三视图中各线条的结构关系，拆分出一些基本几何体的三视图，想象出相应的几何体再组合成所求的几何体．    课堂检测四、巩固训练   1.一个几何体的三视图如图所示，则这个几何体是       (　  　)  C  如图所示，三视图所对应的直观图是(　   　) 2.C3.　一个几何体是由若干个相同的正方体组成的，其主视图和左视图如图所示，则这个几何体最多可由多少个这样的正方体组成     (　   　)A．12个　　B．13个　　C．14个 　　D．18个3.B4．由n个相同的小正方体堆成的几何体，其视图如图所示，则n的最大值是      (　  　)A．18    B．19   C．20    D．214.A 5.长方体的主视图、俯视图如图所示(单位：m)，则其左视图面积是     (　  　) A．4 m2   B．12 m2   C．1 m2   D．3 m25.D6.根据物体的三视图描述物体的形状． 解： 物体是五棱柱形状．如图所示．7．已知某实物的三视图如图所示，描述该实物的形状．解： 观察三视图，可得出物体下部为一个长方体，物体左上部也为一个长方体．综合原三视图可得物体是由两个长方体结合的一个整体(像沙发类)．8.某工厂要加工一批密封罐，设计者给出了密封罐的三视图如图所示，请你按照三视图确定制作每个密封罐所需钢板的面积．【解析】 对于某些立体图形，沿着其中一些线(例如棱柱的棱)剪开，可以把立体图形的表面展开成一个平面图形——展开图．在实际的生产中，三视图和展开图往往结合在一起使用．解决本题的思路是，由三视图想象出密封罐的立体形状，再进一步画出展开图，从而计算面积．解： 由三视图可知，密封罐的形状是正六棱柱(如图所示)．密封罐的高为50 mm，底面正六边形的对角线为100 mm，边长为50 mm，如图所示是它的展开图．由展开图可知，制作一个密封罐所需钢板的面积为6×50×50＋2×6××50×50sin 60°＝6×502×≈27 990(mm2)．   课堂小结      今天我们学习了哪些知识1、简单几何体的三视图。2、由三视图想象立体图。3、借助长方体将三视图还原为立体图                  由三视图确定物体的体积、表面积时，解决问题的关键是恢复原几何体的形状，所以利用形象思维建立空间模型是必备的素养．而在确定小立方块个数时，要把握三种视图之间的关系，巧妙体会“俯视图打地基，主视图疯狂盖，左视图拆违章”的要领，体会几何体构成的所有可能．