浙教版九年级下册3.4 简单几何体的表面展开图获奖ppt课件

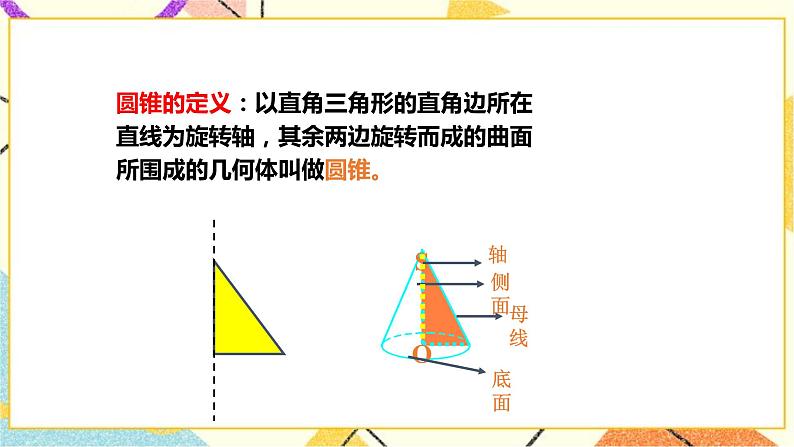
导入新课

   一、创设情景，引出课题

如图，AB，CD旋转所成的面就是圆柱的两个底面，是两个半径相同的圆．AD旋转所成的面就是圆柱的侧面，AD不论转动到哪个位置，都是圆柱的母线．

如果沿圆柱的任意一条母线（MN）把圆柱的侧面“剪开”，铺平，那么就得到圆柱的侧面展开图，如图（2）．这个侧面展开图是一个矩形（矩形ABCD）．这个矩形的一条边（AD）等于圆柱的母线长，也就等于圆柱的高，另一条与它相邻的边（AB）等于底面圆的周长．一般地，一个底面半径为r．母线长为l的圆柱的表面展开图如图（3）所示．

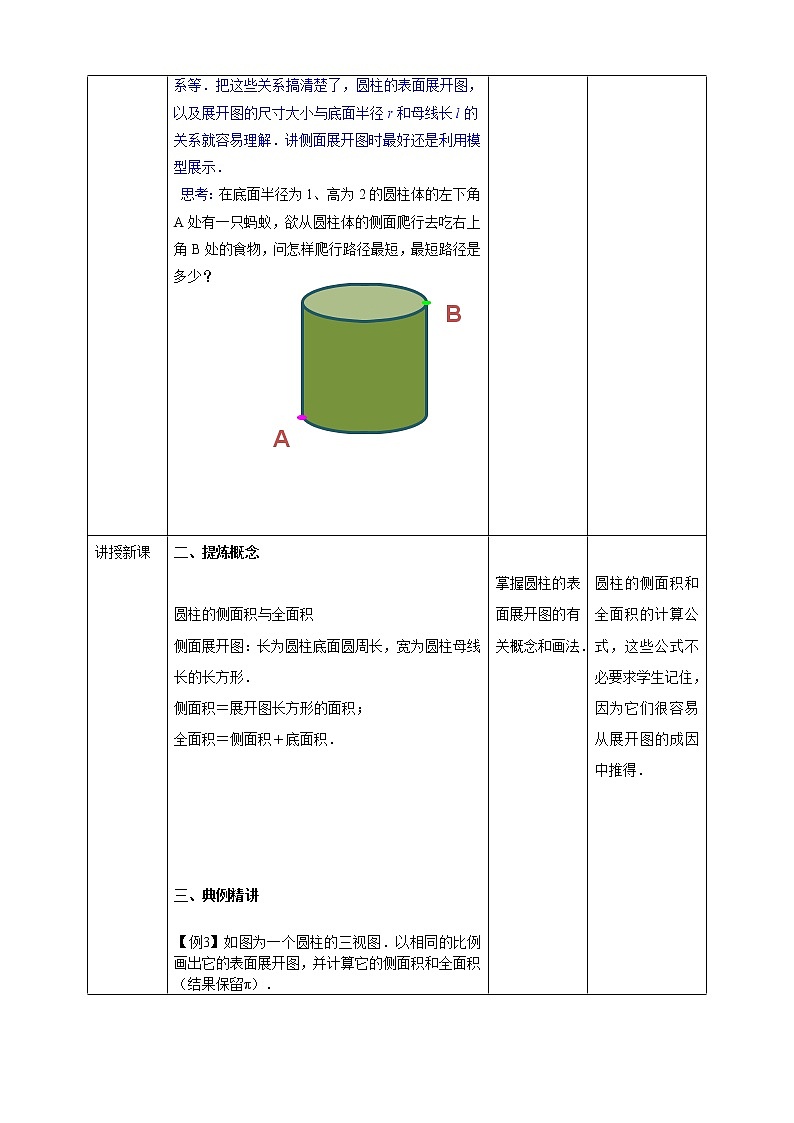
要学生理解圆柱的表面展开图还得从圆柱是怎样一种旋转体说起．利用图（1），讲清圆柱的两个底面是由矩形ABCD的哪两条边旋转一周而成的，圆柱的侧面又是由矩形ABCD的哪条边旋转一周而成的，什么是圆柱的母线，它和圆柱的高有什么关系等．把这些关系搞清楚了，圆柱的表面展开图，以及展开图的尺寸大小与底面半径r和母线长l的关系就容易理解．讲侧面展开图时最好还是利用模型展示．

思考：在底面半径为1、高为2的圆柱体的左下角A处有一只蚂蚁，欲从圆柱体的侧面爬行去吃右上角B处的食物，问怎样爬行路径最短，最短路径是多少？

思考

自议

掌握圆柱侧面展开图，并会求圆柱的侧面积和全面积．

圆柱的表面展开图，以及展开图的尺寸大小与底面半径r和母线长l的关系就容易理解．讲侧面展开图时最好还是利用模型展示．

讲授新课

二、提炼概念

圆柱的侧面积与全面积

侧面展开图：长为圆柱底面圆周长，宽为圆柱母线长的长方形．

侧面积＝展开图长方形的面积；

全面积＝侧面积＋底面积．

三、典例精讲

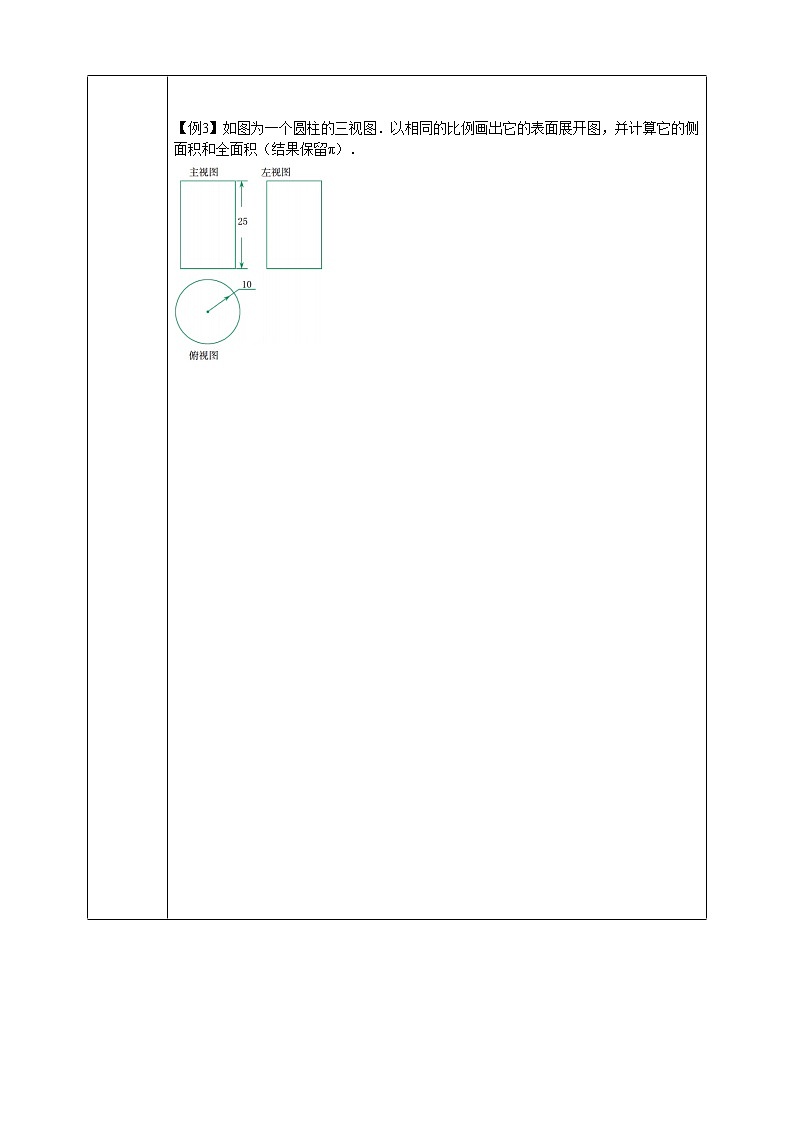
【例3】如图为一个圆柱的三视图．以相同的比例画出它的表面展开图，并计算它的侧面积和全面积（结果保留π）．

分析：由图知．圆柱底面圆的半径r为1cm．母线长l为2.5cm．

因此圆柱的表面展开图中两个底面应画成半径为1cm的圆，侧面展开图应画成长为2πr＝2π×1≈6.28（cm）．宽为2.5cm的长方形．

解：所求圆柱的表面展开图如图．

S侧＝2πrl＝2×π×1×2.5＝5π（cm2）；

S全＝2πr2＋2πrl＝2π×12＋2π×1×2.5＝7π（cm2）．

答：这个圆柱的侧面积为5πcm2，全面积为7πcm2．

理解了圆柱的表面展开图的一般规律后，解例3学生不会有困难，讲解时可把重点放在尺寸的确定上，尤其是侧面展开图的一条边长为2πr，画图时需先算出近似值．本例还给出圆柱的侧面积和全面积的计算公式，这些公式不必要求学生记住，因为它们很容易从展开图的成因中推得．

掌握圆柱的表面展开图的有关概念和画法．

圆柱的侧面积和全面积的计算公式，这些公式不必要求学生记住，因为它们很容易从展开图的成因中推得．

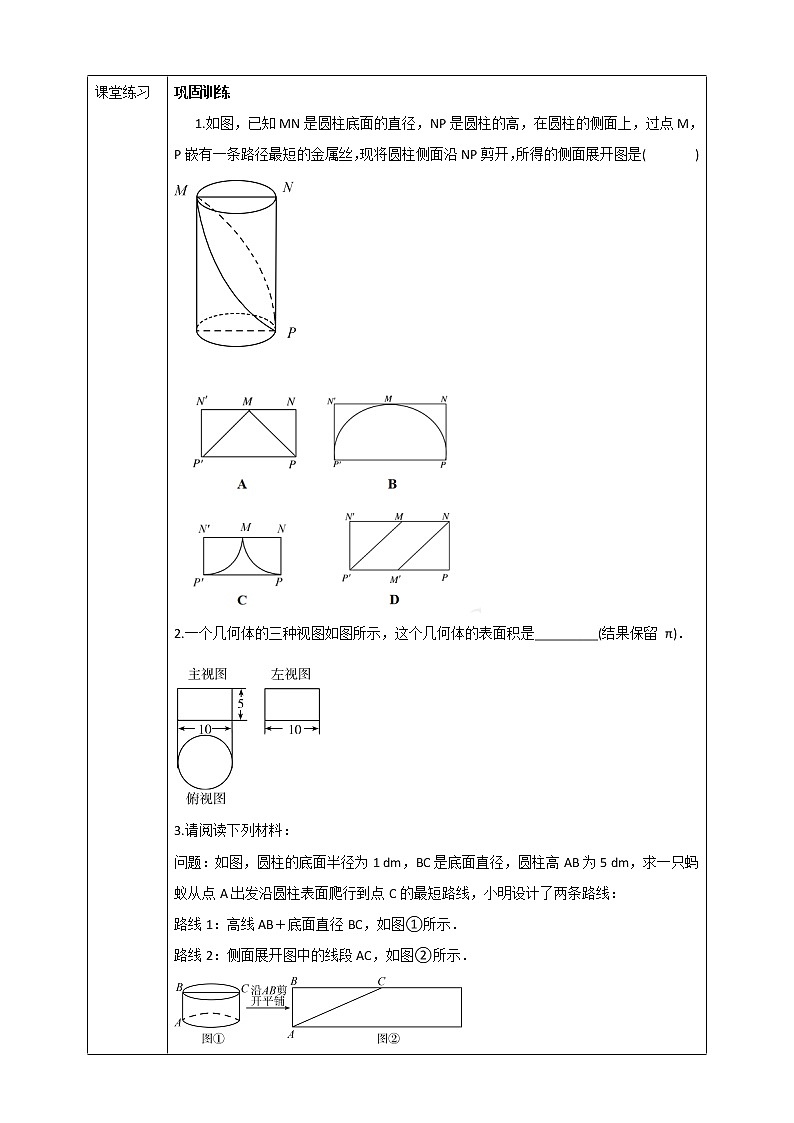
课堂检测

四、巩固训练

  1.如图，已知MN是圆柱底面的直径，NP是圆柱的高，在圆柱的侧面上，过点M，P嵌有一条路径最短的金属丝，现将圆柱侧面沿NP剪开，所得的侧面展开图是(　   　)

A

2.一个几何体的三种视图如图所示，这个几何体的表面积是_________(结果保留 π)．

100  π

3.请阅读下列材料：

问题：如图，圆柱的底面半径为1 dm，BC是底面直径，圆柱高AB为5 dm，求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线，小明设计了两条路线：

路线1：高线AB＋底面直径BC，如图①所示．

路线2：侧面展开图中的线段AC，如图②所示．

(1)设路线1的长度为l1，则l12＝49.设路线2的长度为l2，则l22＝25＋π2.所以选择路线______(填“1”或“2”)较短．

(2)小明把条件改成：“圆柱的底面半径为5 dm，高AB为1 dm”继续按前面的路线进行计算．此时，路线1，l12＝121.路线2，l22＝1＋25 π2.所以选择路线______(填“1”或“2”)较短．

(3)请你帮小明继续研究：当圆柱的底面半径为2 dm，高为h dm时，应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短(结果保留π)．

解：(1)∵49＞25＋π2，

∴选择路线2较短；

(2)∵l12＝121，

l22＝1＋25 π2，

∵l12－l22<0，

∴l12<l22，∴l1<l2，∴选择路线1较短．

(3)当圆柱的底面半径为2 dm，高为h dm时，

l22＝AC2＝AB2＋BC2＝h2＋4 π2，

l12＝(AB＋BC)2＝(h＋4)2，

l12－l22＝h2＋4π2－(h＋4)2＝4 π2－8h－16＝4[(π2－4)－2h]；

当(π2－4)－2h＝0时，即h＝时，l12＝l22；

当h>时，l22<l12，选择路线2，

当h<时，l22>l12，选择路线1.

4.如图，一只蚂蚁在圆柱的底面A处，准备沿着圆柱的侧面爬到B处，它怎样爬行路线最近？先说说你的解题思路，然后给出解答，并算出最近路线的长（精确到0.01 cm）．

解：画出圆柱的侧面展开图如图，

AC＝2π，BC＝6．根据两点之间线段最短，蚂蚁在圆柱表面爬行的最短路成长应是展开图上AB两点之间的距离AB，

AB＝≈8.64（cm）．

答：最近路线的长为8.64cm．

课堂小结

圆柱的侧面积与全面积

侧面展开图：长为圆柱底面圆周长，宽为圆柱母线长的长方形．

侧面积＝展开图长方形的面积；

全面积＝侧面积＋底面积．