山东省潍坊市（青州市、临朐县、昌邑县、诸城市、昌乐县、寿光市）2021-2022学年八年级上学期期中学业质量监测数学试卷(含答案)

2021—2022学年度第一学期期中学业质量监测

八年级数学

注意事项：

1．本试题分为第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷为选择题，52分；第Ⅱ卷为非选择题，98分；共150分．考试时间为120分钟．

2．答卷前务必将试题密封线内及答题卡上面的项目填涂清楚．所有答案都必须涂、写在答题卡相应位置，答在本试卷上一律无效．

第Ⅰ卷（选择题，52分）

一、选择题(本题共8小题，每小题4分，共32分．在每个小题给出的四个选项中，只有一项是符合题目要求的)

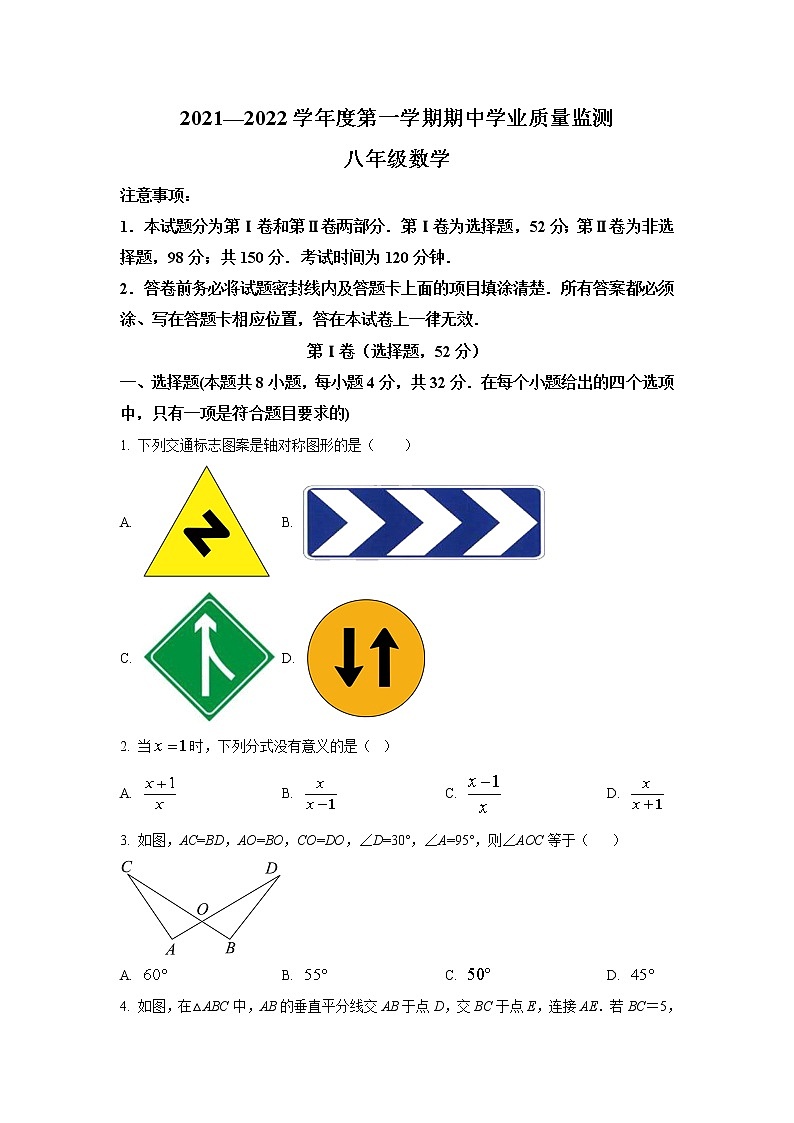
1. 下列交通标志图案是轴对称图形的是（    ）

A.  B.  

C.  D.

2. 当时，下列分式没有意义的是（  ）

A.  B.  C.  D.

3. 如图，AC=BD，AO=BO，CO=DO，∠D=30°，∠A=95°，则∠AOC等于（    ）

A.  B.  C.  D.

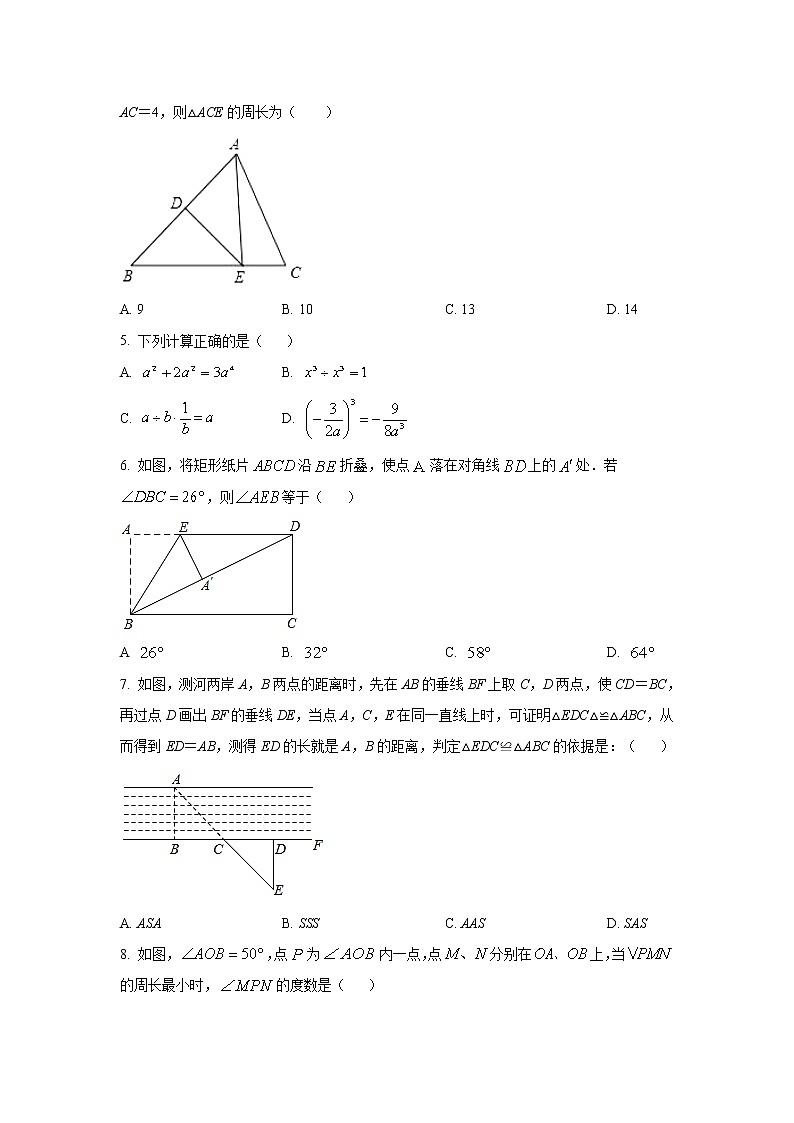
4. 如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC＝5，AC＝4，则△ACE的周长为（　　）

A. 9 B. 10 C. 13 D. 14

5. 下列计算正确的是（    ）

A.  B.  

C.  D.

6. 如图，将矩形纸片沿折叠，使点落在对角线上的处．若，则等于（    ）

A  B.  C.  D.

7. 如图，测河两岸A，B两点的距离时，先在AB的垂线BF上取C，D两点，使CD＝BC，再过点D画出BF的垂线DE，当点A，C，E在同一直线上时，可证明△EDC△≌△ABC，从而得到ED＝AB，测得ED的长就是A，B的距离，判定△EDC≌△ABC的依据是：（    ）

A. ASA B. SSS C. AAS D. SAS

8. 如图，，点为内一点，点分别在上，当的周长最小时，的度数是（    ）

A.  B.  C.  D.

二、选择题(本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分．)

9. 根据分式的基本性质，分式可变形为（    ）

A.  B.  C.  D.

10. 如图，，，要添加一个条件使．添加的条件可以是（    ）

A.  B.  

C.  D.

11. 在古埃及纸草书中，人们把分子为1的分数叫做埃及分数，并且能把一个埃及分数写成两个不相等的埃及分数的和，即．下面利用这个规律计算正确的是（    ）

A.

B.

C.

D.

12. 如图，在△ABC中，∠ABC和∠ACB平分线相交于点O．过点O作EF∥BC交AB于E．交AC于F，过点O作OD⊥AC于D．下列结论正确的是（　　）

A EF＝BE+CF

B. 点O到∠ABC的两边的距离相等

C ∠BOC＝90°+∠A

D 设OD＝m，AE+AF＝n，则S△AEF＝mn

第Ⅱ卷（非选择题，98分）

三、填空题（本大题共4小题，共20分，只要求填写最后结果，每小题填对得5分）

13. 下列分式①②③④⑤中，最简分式有_________（填正确答案的序号）．

14. 等腰三角形的周长为18，其中一条边的长为8，则底边长是_________．

15. 如图，中，，，请依据尺规作图的作图痕迹，计算______．

16. 如图，在平面直角坐标系中，对进行循环往复的轴对称变换，若原来点坐标是，则经过第2021次变换后点的对应点的坐标为_________．

四、解答题（本大题共7小题，共78分．解答要写出必要的文字说明、证明过程或演算步骤）

17. 解方程

（1）        （2）

18. 如图，在平面直角坐标系中，各顶点的坐标分别为：

（1）在图中作△A′B′C′，使△A′B′C′和△ABC关于y轴对称；

（2）写出点A′，B′，C′的坐标；

（3）若△ABC内部一点M(-2，1)关于某条直线的对称点是点M(-2，-5)，写出点E(1，2)关于该条直线的对称点F的坐标．

19. （1）化简：；

（2）已知，且，求的值．

20. △ABC中，AB＝AC，BD平分∠ABC交AC于点D，从点A作AE∥BC交BD的延长线于点E．

（1）若∠BAC＝40°，求∠E的度数；

（2）点F是BE上一点，且FE＝BD．取DF的中点H，请问AH⊥BE吗？试说明理由．

21. 某地对一段长达2400米的河堤进行加固，在加固800米后，采用新的加固模式，每天的工作效率比原来提高25%，用26天完成了全部加固任务．

（1）原来每天加固河堤多少米？

（2）若承包商原来每天支付工人工资为1500元，提高工作效率后每天支付给工人的工资增加了20%，完成整个工程后承包商共支付工人工资多少元？

22. △ABC中，AB＝AC，∠BAC＝90°，点D是直线AB上的一动点（不和A，B重合），BE⊥CD交CD所在的直线于点E，交直线AC于F．

（1）点D在边AB上时，如图，试探索AB、FA和BD之间的等量关系，并说明理由；

（2）点D在AB的延长线或反向延长线上时，请选择一种情况，画出图形，写出AB、FA和BD之间的等量关系，并说明理由．

23. 【阅读材料】

我们知道，任意一个正整数都可以进行这样的分解：（是正整数，且），在的所有这种分解中，如果两因数之差的绝对值最小，我们就称是的最佳分解．并规定：．例如：18可以分解成或，因为，所以是18的最佳分解，所以．

【探索规律】

（1），猜想：_________；

（2），猜想：______________；

【应用规律】

（1）若，其中是正整数，求的值；

（2）若，其中是正整数，求的值．

答案

1-8 BBBAB  CAC  9.AD  10.BD  11.ABD  12.ABC

13. ①③

14. 8或2

15. 81

16.

17. 解：（1）方程的两边同乘以得：，

解得：，                   

经检验，是原方程的解；

（2）将分解因式，原方程化为：

方程两边同乘以得：，               

整理得：

解得：，

检验：当时，

∴是增根，原方程无解．

18. 解：（1）△A′B′C′如图所示，

（2）点A′的坐标为(-4，0)，点B′的坐标为(1，4)，点C′的坐标为(3，1)；

（3）∵点M(-2，1)关于某条直线的对称点是点M(-2，-5)，

∴该直线为y==-2，

∴点E(1，2)关于直线y=－2的对称点F的坐标为(1，-6) ．

19. 解：（1）

；

（2）设，则，

解得：，

∴．

20. 解：（1）∵AB=AC，

∴∠ABC=∠ACB，

∵∠BAC=40°，

∴∠ABC=（180°-∠BAC）=70°，

∵BD平分∠ABC，

∴∠CBD=∠ABC=35°，

∵AE∥BC，

∴∠E=∠CBD=35°；

（2）∵BD平分∠ABC，∠E=∠CBD，

∴∠CBD=∠ABD=∠E，

∴AB=AE，

在△ABD和△AEF中，

，

∴△ABD≌△AEF（SAS），

∴AD=AF，

∵点H是DF的中点，

∴AH⊥BE．

21. 解：（1）设原来每天加固河堤米，则采用新的加固模式后每天加固米．      

根据题意得：，

解这个方程得：

经检验可知，是原分式方程的根，并符合题意；

答：原来每天加固河堤80米；

（2）（米）

所以，承包商支付给工人的工资为：（元）．

22. 解：（1）AB=FA+BD，理由如下：

∵BE⊥CD，

∴∠BEC=90°=∠BAC，

∴∠F+∠FBA=90°，∠F+∠FCE=90°，

∴∠FBA=∠FCE，

∵∠FAB=180°-∠DAC=90°，

∴∠FAB=∠DAC，

在△FAB和△DAC中，

，

∴△FAB≌△DAC（ASA），

∴FA=DA，

∴AB=AD+BD=FA+BD；

（2）解：点D在AB的延长线上时，AB=AF-BD；点D在AB的反向延长线上时，AB=BD-AF．

理由如下：

①当点D在AB的延长线上时，如图2．

同（1）得：△FAB≌△DAC（ASA），

∴FA=DA．

∴AB=AD-BD=AF-BD；

②点D在AB的反向延长线上时，如图3．

同（1）得：△FAB≌△DAC（ASA），

∴FA=DA，

∴AB=BD-AD=BD-AF．

23. 解：探索规律

（1）∵f(6)=f(23)=，f(15)=f(35)=，f(24)=f(46)==，

∴f()=f=；

（2）∵f(4)=f(22)=1，f(9)=f(32)=1，f(25)=f(52)=1，

∴f()=1；

应用规律

（1）∵f()=f=，且f()=，

∴，

∴1011x=1010x+2020，

解得：x=2020，

经检验，x=2020符合题意，所以x的值是2020；

（2）由，可设（为正整数），

即，所以，

①当时，，解得，不符合题意，舍去；

②当时，，解得，符合题意；

③当时，，无意义，舍去；

④当时，，解得，不符合题意，舍去；

⑤当时，，解得，不符合题意，舍去；

综上，的值是5．