2023年 九年级数学中考复习 几何图形变换综合压轴题 专题训练

这是一份2023年 九年级数学中考复习 几何图形变换综合压轴题 专题训练，共54页。
2023年春九年级数学中考复习《几何图形变换综合压轴题》专题训练（附答案）
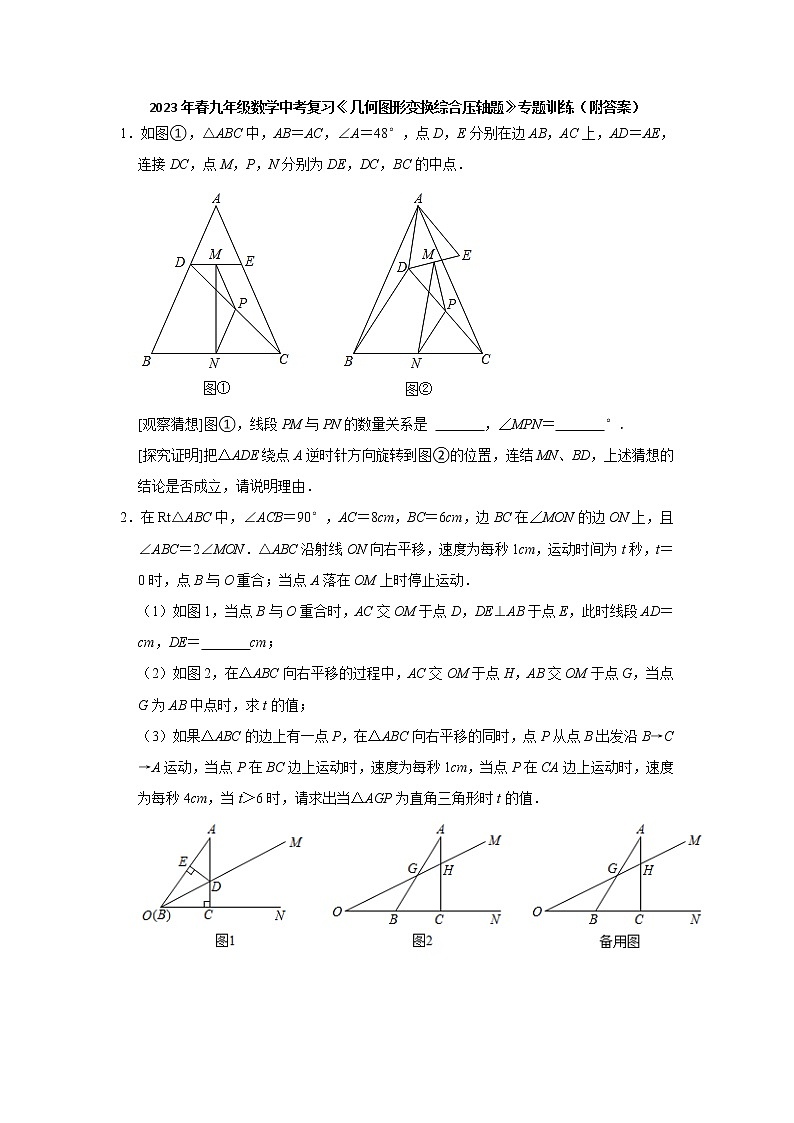
1．如图①，△ABC中，AB＝AC，∠A＝48°，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．

[观察猜想]图①，线段PM与PN的数量关系是 　 　，∠MPN＝　 　°．
[探究证明]把△ADE绕点A逆时针方向旋转到图②的位置，连结MN、BD，上述猜想的结论是否成立，请说明理由．
2．在Rt△ABC中，∠ACB＝90°，AC＝8cm，BC＝6cm，边BC在∠MON的边ON上，且∠ABC＝2∠MON．△ABC沿射线ON向右平移，速度为每秒1cm，运动时间为t秒，t＝0时，点B与O重合；当点A落在OM上时停止运动．
（1）如图1，当点B与O重合时，AC交OM于点D，DE⊥AB于点E，此时线段AD＝　 　cm，DE＝　 　cm；
（2）如图2，在△ABC向右平移的过程中，AC交OM于点H，AB交OM于点G，当点G为AB中点时，求t的值；
（3）如果△ABC的边上有一点P，在△ABC向右平移的同时，点P从点B出发沿B→C→A运动，当点P在BC边上运动时，速度为每秒1cm，当点P在CA边上运动时，速度为每秒4cm，当t＞6时，请求出当△AGP为直角三角形时t的值．



3．如图，Rt△ABC，∠BAC＝90°，AB＝AC，Rt△CDE，∠CDE＝90°，CD＝DE，（AB＝AC＞EC）．连接AD，以AD为腰作等腰Rt△ADF，∠ADF＝90°，AD＝DF，连接BF，AE交于点G．
（1）如图①，当点D在线段AC上，点E在线段BC上时，直接写出线段AG，GE的数量关系：　 　；
（2）如图②，当Rt△CDE绕点C顺时针旋转α（0°＜α＜45°）时，（1）中的结论还成立吗？若成立请证明；若不成立，请说明理由．
（3）当Rt△CDE绕点C顺时针旋转一周回到图①位置，若CD＝DE＝2，问正好在旋转一周的过程中，点G所经过的路径长为S，请直接写出S的值．

4．如图①，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，点D，E，N分别是△ABC的AB，AC，BC边上的中点，连接AN，DE交于点M．
（1）观察猜想：
的值为 　 　；BD与CE的位置关系是 　 　．
（2）探究与证明：
将△ADE绕点A按顺时针方向旋转α角（0°＜α＜360°），且△ADE内部的线段AM随之旋转，如图②所示，连接BD，CE，MN，试探究线段BD与MN之间分别有什么样的数量关系，以及BD与CE有什么样的位置关系，并证明；
（3）拓展与延伸：
△ADE在旋转的过程中，设直线CE与BD相交于点F，当∠CAE＝90°时，请直接写出BF的值．

5．如图，在等腰直角△ABC中，∠ACB＝90°，AB＝7，点D，E分别在边AB，BC上，将线段ED绕点E按逆时针方向旋转90°得到EF．
（1）如图1，若AD＝BD，点E与点C重合，AF与DC相交于点O，求证：BD＝2DO．
（2）已知点G为AF的中点．
①如图2，若AD＝BD，CE＝2，求DG的长．
②若AD＝6BD，是否存在点E，使得△DEG是直角三角形？若存在，求CE的长，若不存在，试说明理由．

6．等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，AB＝4，AE＝2，其中△ABC固定，△ADE绕点A作360°旋转，点F、M、N分别为线段BE、BC、CD的中点，连接MN、NF．
问题提出：
（1）如图1，当AD在线段AC上时，则∠MNF的度数为 　 　；线段MN和线段NF的数量关系为 　 　．
深入讨论：
（2）如图2，当AD不在线段AC上时，请求出∠MNF的度数及线段MN和线段NF的数量关系 　 　；
拓展延伸：
（3）如图3，△ADE持续旋转过程中，若CE与BD交点为P，则△BCP面积的最小值为 　 　．


7．已知△ABC中，∠C＝90°，AC＝BC＝4，直角∠EPF的顶点P为斜边AB上的一个动点，直角的两边分别交线段AC、BC于E、F两点．
（1）如图1，当PB＝3AP，且PF⊥BC时，求PF的长度；
（2）如图2，当AP＝PB时，求证：PE＝PF；
（3）如图3，在（2）的条件下，将直角∠EPF绕点P旋转，点D是EP的中点，连接DF，过点C作CN⊥DF，垂足为M，交PF于N；当线段DF最短时，求三角形MNF的面积．

8．（1）如图1，∠BAD的平分线AE与∠BCD的平分线CE交于点E，AB∥CD，∠BAE＝25°，∠DCE＝20°，求∠AEC的度数；

（2）如图2，∠BAD的平分线AE与∠BCD的平分线CE交于点E，∠ADC＝α°，∠ABC＝β°，求∠AEC的度数；
（3）如图3，PQ⊥MN于点O，点A是平面内一点，AB、AC交MN于B、C两点，AD平分∠BAC交PQ于点D，请问的值是否发生变化？若不变，求出其值；若改变，请说明理由．



9．如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，BC＝，摆动臂AD可绕点A旋转，AD＝．
（1）在旋转过程中，
①当A、D、B三点在同一直线上时，求BD的长；
②当A、D、B三点为同一直角三角形的顶点时，求BD的长．
（2）若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D1转到其内的点D2处，如图2，此时∠AD2C＝135°，CD2＝1，求BD2的长；
（3）如图3，若连接（2）中的D1D2，将（2）中△AD1D2的形状和大小保持不变，把△AD1D2绕点A在平面内自由旋转，分别取D1D2、CD2、BC的中点M、P、N，连接MP、PN、NM，M随着△AD1D2绕点A在平面内自由旋转，△MPN的面积是否发生变化，若不变，请直接写出△MPN的面积；若变化，△MPN的面积是否存在最大与最小？若存在，请直接写出△MPN面积的最大值与最小值．

10．如图①在△ABC中，∠ACB＝90°，AC＝BC，点D是AB边上的动点，DE⊥BC于点E，连接AE，CD，点F，G，H分别是AE，CD，AC的中点．
（1）观察猜想：△FGH的形状是 　 　．
（2）探究论证：把△BDE绕点B按逆时针方向旋转到图②的位置，（1）中的结论是否仍然成立？请说明理由．
（3）拓展延伸：把△BDE绕点B在平面内自由旋转，若BC＝6，BE＝2，请直接写出△FGH周长的取值范围．

11．如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC，DE是△ABC的中位线，AN⊥BC，垂足为N，交DE于点M．
（1）观察猜想
图①中，的值为 　 　；的值为 　 　．
（2）探究证明
如图②，将△ADE绕点A顺时针旋转，旋转角为a（0°＜a＜360°），连接BD，CE，判断BD与CE和BD与MN分别有什么样的数量关系，并证明；
（3）拓展延伸
在△ADE旋转的过程中，设直线CE与BD相交于点F，若∠CAE＝90°，AB＝6，请直接写出此时线段BF的长．

12．（一）发现探究：
如图1，矩形ABCD和矩形AEFG位似，AB：BC＝：1，连接AC，则线段BE与CF有何数量关系，关系是 　 　；直线BE与直线CF所夹锐角的度数是 　 　．
（二）拓展探究：
如图2，将矩形AEFG绕点A逆时针旋转角α（0°＜α＜360°），上面的结论是否仍然成立？如果成立，请就图2给出的情况加以证明．
（三）问题解决：
若点M是CF的中点，连接GM，BC＝4，AE＝AB，在矩形AEFG绕点A旋转过程中，请直接写出GM长的取值范围．

13．已知△ABC中，点E为AB的中点，将△AEC沿CE所在的直线折叠得△A'EC，过点B作BF//AC，交直线A'C于点F．
（1）如图1，若∠ACB＝90°，∠A＝30°，则线段AC，CF，BF之间的数量关系为．
（2）如图2，若∠ACB为任意角，写出此时AC，CF，BF之间的数量关系，并证明．
（3）如图3，若∠ACB＝120°，BF＝6，BC＝4，求线段AC的长．


14．在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点，连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．
（1）猜想观察：如图1，若α＝60°，BD交AC于点M，则的值是 　 　，直线BD与直线CP相交所成的较小角的度数是 　 　．
（2）类比探究：如图2，若α＝90°，BD与AC，PC分别相交于点M，N．求的值及∠CNM的度数．
（3）解决问题：如图3，当α＝90°时，若P，D，C三点在同一直线上，且DA＝DC，BD交AC于点M，DM＝2﹣，求AP的长．

15．（1）观察发现：如图1，在△ABC中，AC＝BC，∠ACB＝90°，点D是∠ACB的平分线CM上一点，将线段CD绕点C逆时针旋转90°到CE，连结BE、BD，DE交BC于F．
填空：
①线段BD与BE的数量关系是 　 　；
②线段BC与DE的位置关系是 　 　．
（2）拓展探究：如图2，在△ABC中，AC＝BC，∠ACB＝α，点D是边AB的中点，将CD绕点C逆时针旋转α到CE，连结BE、DE，DE交BC于F．（1）中的结论是否仍然成立？请说明理由．
（3）拓展应用：如图3，在△ABC中，AB＝AC，∠BAC＝60°，BC＝2，∠ACB的平分线交AB于D，点E是射线CD上的一点，将CE绕点C顺时针旋转60°到CF，连结AE、AF、EF，EF与AC相交于G，若以A、F、G为顶点的三角形与△ADE全等，直接写出EF的长．

16．[初步尝试]
（1）如图①，在三角形纸片ABC中，∠ACB＝90°，将△ABC折叠，使点B与点C重合，折痕为MN，则AM与BM的数量关系为 　 　；
[思考说理]
（2）如图②，在三角形纸片ABC中，AC＝BC＝6，AB＝10，将△ABC折叠，使点B与点C重合，折痕为MN，求的值；
[拓展延伸]
（3）如图③，在三角形纸片ABC中，AB＝9，BC＝6，∠ACB＝2∠A，将△ABC沿过顶点C的直线折叠，使点B落在边AC上的点B′处，折痕为CM．
①求线段AC的长；
②若点O是边AC的中点，点P为线段OB′上的一个动点，将△APM沿PM折叠得到△A′PM，点A的对应点为点A′，A′M与CP交于点F，求的取值范围．

17．如图，在平面直角坐标系中，O为坐标原点，△ABC的边BC落在x轴上，顶点A在y轴正半轴上，点B在x轴负半轴上，点C在x轴正半轴上，若BC＝6，∠BAC+∠ACB＝90°．
（1）求点C坐标；
（2）现有一动点P从点B出发，以2个单位长度/秒的速度，沿线段BA向点A运动，运动时间为t秒，点D为y轴负半轴上一点，连接DP、DC，将线段CD绕点C旋转，使点D落在线段OB上于点E，若∠ADC﹣∠CAD＝2∠ADP，请用含t的代数式表示点E坐标；
（3）在（2）的条件下，点F为线段OC上一点，连接PF并延长，交射线AC于点G，连接DE、DG，若PG＝2FG，∠EDG＝120°，AP＝1，求t的值．






18．△ABC为等边三角形，AB＝4，AD⊥BC于点D，E为线段AD上一点，AE＝．以AE为边在直线AD右侧构造等边三角形AEF，连接CE，N为CE的中点．
（1）如图1，EF与AC交于点G，连接NG，求线段NG的长；
（2）如图2，将△AEF绕点A逆时针旋转，旋转角为α，M为线段EF的中点，连接DN，MN．当30°＜α＜120°时，猜想∠DNM的大小是否为定值，并证明你的结论；
（3）连接BN，在△AEF绕点A逆时针旋转过程中，当线段BN最大时，请直接写出△ADN的面积 　 　．
19．已知：如图1，Rt△ABC中，∠ACB＝90°，CA＝CB，等边△CDE的边CE在CB上，点D在AB上．
（1）求证：∠ACD＝2∠BDE；
（2）如图2，将△ADC沿着CD翻折，得到△CDF．连接EF，求证：AD＝EF；
（3）如图3，在（2）的条件下，过点D作DG⊥CD交CB延长线于点G，若BE＝m，DG＝4+2m．求△FDE的面积．




20．已知，△ABC中，AB＝AC＝2，BC＝2，∠A＝90°．取一块含45°角的直角三角尺，将直角顶点放在斜边BC边的中点O处，一条直角边过A点（如图1）．三角尺绕O点顺时针方向旋转，使90°角的两边与Rt△ABC的两边AB，AC分别相交于点E，F（如图2）．设BE＝x，CF＝y．
（1）探究：在图2中，线段AE与CF有怎样的大小关系？证明你的结论；
（2）求在上述旋转过程中y与x的函数关系式，并写出x的取值范围；
（3）若将直角三角尺45°角的顶点放在斜边BC边的中点O处，一条直角边过A点（如图3）．三角尺绕O点顺时针方向旋转，使45°角的两边与Rt△ABC的两边AB，AC分别相交于点E，F（如图4）．在三角尺绕O点旋转的过程中，△OEF是否能成为等腰三角形？若能，直接写出△OEF为等腰三角形时x的值；若不能，请说明理由．


参考答案
1．解：[观察猜想]如图①中，

∵AB＝AC，AD＝AE，
∴AB﹣AD＝AC﹣AE，
∴BD＝CE，
∵点M、P、N分别为DE、DC、BC的中点，
∴PM，PN分别是△DEC，△CDB的中位线，
∴PM＝CE，PN＝BD，且PM∥CE，PN∥BD，
∴PM＝PN，∠DPM＝∠ACD，∠PNC＝∠B，
∵∠DPN＝∠BCD+∠PNC＝∠BCD+∠B，
∴∠MPN＝∠DPM+∠DPN＝∠ACD+∠BCD+∠B＝∠ACB+∠B，
∵∠BAC＝48°，
∴∠ACB+∠B＝180°﹣48°＝132°，
∴∠MPN＝132°，
故答案为：PM＝PN，132．

[探究证明]：成立．
理由：如图②中，连接CE，

由旋转得∠BAD＝∠CAE，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS），
∴BD＝CE，∠ABD＝∠ACE，
∵点M、P、N分别为DE、DC、BC的中点，
∴PM，PN分别是△DEC，△CDB的中位线，
∴PM＝CE，PN＝BD，
∴PM＝PN，
∵PM∥CE，PN∥BD，
∴∠DPM＝∠DCE，∠PNC＝∠DBC，
∵∠DPN＝∠PNC+∠DCB＝∠DBC+∠DCB，
∴∠NPM＝∠DPM+∠DPN＝∠DCE+∠DBC+∠DCB，
∵∠DCE＝∠ACD+∠ACE＝∠ACD+∠ABD，
∴∠MPN＝∠ACD+∠ABD+∠DBC+∠DCB＝∠ABC+∠ACB，
∵∠ABC+∠ACB＝180°﹣48°＝132°，
∴∠MPN＝132°．
∴PM＝PM，∠MPN＝132°，
∴（1）中结论成立．

2．解：（1）如图1中，∵∠ACB＝90°，AC＝8cm，BC＝6cm，
∴AB＝＝＝10（cm），
∵∠ABC＝2∠MON，
∴∠DOE＝∠DOC，
∵∠OED＝∠OCD＝90°，OD＝OD，
∴△ODE≌△ODC（AAS），
∴OC＝OD＝6，DE＝CD，
∴AE＝OA﹣OE＝10﹣6＝4（cm），
设DE＝CD＝x，
在Rt△ADE中，AE2+DE2＝AD2，
∴42+x2＝（8﹣x）2，
∴x＝3，
∴DE＝3cm，AD＝8﹣3＝5cm，
故答案为：5，3；

（2）∵∠ABC＝2∠MON，∠ABC＝∠O+∠BGO，
∴∠O＝∠BGO，
∴BO＝BG，
∵G是AB的中点，
∴AG＝BG＝5cm，
∴OB＝BG＝5cm，
∴t＝5；

（3）当t＞6时，点P在AC边上
此时BG＝OB＝tcm，AG＝（10﹣t）cm，AP＝AC﹣PC＝8﹣4（t﹣6）＝（32﹣4t）cm，
①当∠AP′G＝90°时，如图3中，△AGP′∽△ABC，
∴＝，
即＝，
解得t＝7.5；

②当∠AGP″＝90°时，如图3中，△AGP″∽△ACB，
∴＝，
即＝，
解得t＝
综上，t的值为7.5或．

3．解：（1）∵Rt△ABC，∠BAC＝90°，AB＝AC，Rt△CDE，∠CDE＝90°，CD＝DE，
∴∠BAC＝∠CDE，∠ABC＝∠DEC＝45°，
∴AB∥EF，AF∥BE，
∴四边形ABEF是平行四边形，
∴AG＝GE，
故答案为：AG＝GE；
（2）仍然成立，理由如下：
如图②，连接EF，BE，

∵∠ADF＝∠EDC＝90°，
∴∠ADC＝∠EDF，
又∵AD＝DF，DE＝DC，
∴△ADC≌△EDF（SAS），
∴EF＝AC，∠DAC＝∠EFD，
∴AB＝EF，
∵∠BAC＝90°，∠DAF+∠AFD＝90°，
∴∠BAC+∠DAF+∠AFD＝180°，
∴∠BAC+∠DAF+∠DAC+∠AFE＝180°，
∴∠BAF+∠AFE＝180°，
∴AB∥EF，
∴四边形ABEF是平行四边形，
∴AG＝GE；
（3）如图③，取AC中点H，连接GH，

∵CD＝DE＝2，∠EDC＝90°，
∴EC＝2，
∵AG＝GE，AH＝HC，
∴GH＝EC＝，
∵当Rt△CDE绕点C顺时针旋转一周回到图①位置，
∴点G绕点H顺时针旋转一周，
∴点G所经过的路径长为S＝2π．
4．解：（1）∵∠BAC＝90°，AB＝6，AC＝8，
∴BC＝＝＝10，
∵点N是BC上的中点，
∴AN＝BC＝5
∵DE∥BC
∴＝，
∴＝＝．
∵∠BAC＝90°，
∴AB⊥AC，
∴BD⊥CE，
故答案为：，垂直；

（2）结论：＝，＝．理由如下：由图1可得：
∵DE∥BC
∴△ADE∽△ABC，△ADM∽△ABN，
∴＝，＝，
∵将△ADE绕点A按顺时针方向旋转α角
∴∠DAB＝∠CAE＝α，且＝，
∴△ADB∽△AEC
∴＝＝＝，
∵∠BAD＝∠MAN＝α，且＝，
∴△ABD∽△ANM
∴＝＝；

（3）如图，当点E在线段AB上时，

∵AB＝6，AC＝8，AE＝4，AD＝3
∴CD＝11，BD＝
√
AD2+AB2
＝＝3，CE＝＝＝4，
∵＝＝，
∴＝，且∠DAE＝∠EAC＝90°
∴△AEC∽△ADB
∴∠ABD＝∠ACE，且∠ABD+∠BDA＝90°，
∴∠ACE+∠BDA＝90°
∴∠DFC＝90°＝∠BAC，且∠ACE＝∠ACE
∴△ACE∽△FCD
∴＝．
∴DF＝×4＝，
∴BF＝BD﹣DF＝．
如图，当点E在线段BA的延长线上，

同理可得：BD＝3，BE＝10，∠BAC＝∠EFB＝90°
∵∠EBF＝∠EBF，∠BAD＝∠EFB＝90°
∴△ADB∽△FEB
∴＝，
∴BF＝＝4，
综上所述：当∠CAE＝90°时，BF＝4或．
5．（1）证明：∵CA＝CB，∠ACB＝90°，BD＝AD，
∴CD⊥AB，CD＝AD＝BD，
∵CD＝CF，
∴AD＝CF，
∵∠ACD＝∠DCF＝90°，
∴AD∥CF，
∴四边形ADFC是平行四边形，
∴OD＝OC，
∴BD＝2OD；

（2）解：①如图2中，作DT⊥BC于点T，FH⊥BC于H，连接BF，

则∠DTE＝∠EHF＝90°，
∴∠TDE+∠DET＝90°，
∵∠DET+∠HEF＝90°，
∴∠TDE＝∠HEF，
又∵DE＝EF，
∴△DTE≌△EHF（AAS），
∴DT＝EH，
由题意：BD＝AD＝CD＝AB＝，BC＝BD＝7，
∵DT⊥BC，
∴EH＝DT＝TC＝，
∵EC＝2，
∴BH＝BC﹣HE﹣EC＝，
∴HF＝TE＝TC﹣EC＝BC﹣EC＝，
∴BF＝＝，
∵点D、G分别是AB、AF的中点，
∴DG＝BF＝；

②存在，
理由：如图3﹣1中，当∠DEG＝90°时，F，E，G，A共线，作DT⊥BC于点T，FH⊥BC于H．设EC＝x．

∵AD＝6BD，
∴BD＝AB＝，
∵DT⊥BC，∠DBT＝45°，
∴DT＝BT＝1，
∵△DTE≌△EHF，
∴EH＝DT＝1，
∴BH＝FH＝6﹣x，
∵FH∥AC，
∴＝，
∴＝，
整理得：x2﹣6x+7＝0，
解得x＝3±．
∴EC＝3±．
如图3﹣2中，当∠EDG＝90°时，取AB的中点O，连接OG．作EH⊥AB于H．

设EC＝x，由2①可知BF＝（6﹣x），OG＝BF＝（6﹣x），
∵∠EHD＝∠EDG＝∠DOG＝90°，
∴∠ODG+∠OGD＝90°，∠ODG+∠EDH＝90°，
∴∠DGO＝∠HDE，
∴△EHD∽△DOG，
∴＝，
∴＝，
整理得：x2﹣18x+134＝0，
解得x＝9﹣或9+（舍弃）．
∴EC＝9﹣．
如图3﹣3中，当∠DGE＝90°时，取AB的中点O，连接OG，CG，作DT⊥BC于T，FH⊥BC于H，EK⊥CG于K．设EC＝x．

∵∠DBE＝∠DFE＝45°，
∴D，B，F，E四点共圆，
∴∠DBF+∠DEF＝180°，
∵∠DEF＝90°，
∴∠DBF＝90°，
∵AO＝OB，AG＝GF，
∴OG∥BF，
∴∠AOG＝∠ABF＝90°，
∴OG⊥AB，

∵OG垂直平分线段AB，
∵CA＝CB，
∴O，G，C共线，
由△DTE≌△EHF，可得EH＝DT＝BT＝1，ET＝FH＝6﹣x，BF＝（6﹣x），OG＝BF＝（6﹣x），CK＝EK＝x，GK＝﹣（6﹣x）﹣x，
由△OGD∽△KEG，可得＝，
∴＝，
解得x＝1，
∴EC＝1．
综上所述，满足条件的EC的值为3±或9﹣或1．
6．解：（1）如图1中，连接DB，MF，CE，延长BD交EC于H．

∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，
∴△BAD≌△CAE（SAS），
∴BD＝EC，∠ACE＝∠ABD，
∵∠ABD+∠ADB＝90°，∠ADB＝∠CDH，
∴∠ADH+∠DCH＝90°，
∴∠CHD＝90°，
∴EC⊥BH，
∵BM＝MC，BF＝FE，
∴MF∥EC，MF＝EC，
∵CM＝MB，CN＝ND，
∴MN∥BD，MN＝BD，
∴MN＝MF，MN⊥MF，
∴∠NMF＝90°，
∴∠MNF＝45°，NF＝MN，
故答案为：45°，NF＝MN；
（2）如图2中，连接MF，EC，BD．设EC交AB于O，BD交EC于H．

∵AC＝AB，AE＝AD，∠BAD＝∠CAE＝90°，
∴∠BAD＝∠CAE，
∴△BAD≌△CAE（SAS），
∴BD＝EC，∠ACE＝∠ABD，
∵∠AOC+∠ACO＝90°，∠AOC＝∠BOH，
∴∠OBH+∠BOH＝90°，
∴∠BHO＝90°，
∴EC⊥BD，
∵BM＝MC，BF＝FE，
∴MF∥EC，MF＝EC，
∵CM＝MB，CN＝ND，
∴MN∥BD，MN＝BD，
∴MN＝MF，MN⊥MF，
∴∠NMF＝90°，
∴∠MNF＝45°，NF＝MN．
故答案为：NF＝MN；
（3）如图3中，以A为圆心AD为半径作⊙A．

当直线PB与⊙A相切时，此时∠CBP的值最小，点P到BC的距离最小，即△BCP的面积最小，
∵AD＝AE，AB＝AC，∠BAC＝∠DAE＝90°，
∴∠BAD＝∠CAE，
∴△BAD≌△CAE（SAS），
∴∠ACE＝∠ABD，BD＝EC，
∵∠ABD+∠AOB＝90°，∠AOB＝∠CPO，
∴∠CPB＝90°，
∵PB是⊙A的切线，
∴∠ADP＝90°，
∵∠DPE＝∠ADP＝∠DAE＝90°，
∴四边形ADPE是矩形，
∵AE＝AD，
∴四边形ADPE是正方形，
∴AD＝AE＝PD＝PE＝2，BD＝EC＝＝2，
∴PC＝2﹣2，PB＝2+2，
∴S△BCP的最小值＝×PC×PB＝（2﹣2）（2+2）＝4．
故答案为：4．
7．（1）解：∵PE⊥AC，
∴∠AEP＝∠PEC＝90°．
又∵∠EPF＝∠ACB＝90°，
∴四边形PECF为矩形，
∴∠PFC＝90°，
∴∠PFB＝90°，
∴∠AEP＝∠PFB．
∵AC＝BC，∠C＝90°，
∴∠A＝∠B＝45°，
∴∠FPB＝∠B＝45°，
∴PF＝BF，
∵PB＝3AP，BA＝4，
∴PB＝3，
∵PF2+BF2＝，
∴PF＝3；
（2）证明：连接PC，如图2．

∵∠ACB＝90°，CA＝CB，
∴CP＝AP＝AB．∠ACP＝∠BCP＝∠ACB＝45°，CP⊥AB，
∴∠APE+∠CPE＝90°．
∵∠CPF+∠CPE＝90°，
∴∠APE＝∠CPF．
在△APE和△CPF中，
，
∴△APE≌△CPF（ASA），
∴PE＝PF．
（3）解：由（2）可知△PEF是等腰直角三角形，当PF⊥CB时，线段DF最短，

∴四边形PECF是正方形，
∴CF＝PF，
∵AP＝BP＝2，
∴PF＝BF＝CF＝2，
∵CN⊥DF，
∴∠MCF+∠MFC＝90°，
∵∠MFC+∠DFP＝90°，
∴∠MCF＝∠DFP，
∵∠CFN＝∠DPF，
∴△CFN≌△FPD（ASA），
∴FN＝DP＝1，
∴＝，
∵，
∴MF＝＝＝，
∴MN＝＝，
∴＝＝．
8．解：（1）如图1，过点E作EM∥AB，

∵AB∥CD，
∴EM∥AB∥CD，
∴∠DCE＝∠CEM，∠BAE＝∠AEM，
∵∠BAE＝25°，∠DCE＝20°，
∴∠AEC＝∠CEM+∠AEM＝∠DCE+∠BAE＝25°+20°＝45°；
（2）如图2，延长BC交AD于点F，

∵∠BFD＝∠B+∠BAD，∠BCD＝∠BFD+∠D，
∴∠BCD＝∠BFD+∠D＝∠B+∠BAD+∠D，
∵CE平分∠BCD，AE平分∠BAD，
∴∠ECD＝∠ECB＝∠BCD，∠EAD＝∠EAB＝∠BAD，
∵∠AEC+∠ECB＝∠ABC+∠EAB，
∴∠AEC＝∠ABC+∠EAB﹣∠ECB＝∠ABC+∠EAB﹣∠BCD＝∠ABC+∠EAB﹣（∠ABC+∠BAD+∠ADC）＝（∠ABC﹣∠ADC）＝（β﹣α），
即∠AEC＝；
（3）的值不发生变化，其值为，理由如下：
如图3，记AB与PQ交于E，AD与CB交于F，

∵AD平分∠BAC，
∴∠BAD＝∠DAC，
∵PQ⊥MN，
∴∠DOF＝∠BOE＝90°，
∵∠DOF+∠ADP＝∠DAC+∠ACB①，∠ADP+∠DFO＝∠OEB+∠ABC②，
所以①﹣②得，
90°﹣∠DFO＝∠DAC+∠ACB﹣∠OEB﹣ABC，
∴90°﹣∠DFO+（∠OEB﹣∠DAC）＝∠ACB﹣ABC，
∴∠ADP+∠ADP＝∠ACB﹣ABC，
∴2∠ADP＝∠ACB﹣ABC，
∴＝．
9．解：（1）∵AB＝AC，BC＝，∠BAC＝90°，
∴AB＝AC＝，
①当点D落在线段AB上，
BD＝AB﹣AD＝﹣，
当点D落在线段BD的延长线上时，
BD＝AB+AD＝+，
∴BD的长为﹣或+．
②显然∠ABD不能为直角，
当∠ADB为直角时，AD2+BD2＝AB2，
∴BD＝，
当∠BAD为直角时，AB2+AD2＝BD2，
∴BD＝，
∴BD长为或．
（2）如图，连接D1D2，D1C，则△AD1D2为等腰直角三角形，

∴D1D2＝AD1＝2，
∴AD1＝AD2，AB＝AC，
∵∠BAC＝∠D2AD1，
∴∠BAD2＝∠CAD1，
在△ABD2和△ACD1中，
，
∴△BAD2≌△CAD1（SAS），
∴BD2＝CD1，
又∵∠AD2C＝135°，
∴∠D1D2C＝∠AD2C﹣∠AD2D1＝135°﹣45°＝90°，
∴CD1＝＝，
∴BD2＝；
（3）△MPN的面积存在最大值与最小值，理由如下：
如图2，所示，连接CD1，

理由：∵点P，M分别是CD2，D2D1的中点，
∴PM＝CD1，PM∥CD1，
∵点N，M分别是BC，D1D2的中点，
∴PN＝BD2，PN∥BD2，
∵BD2＝CD1，
∴PM＝PN，
∴△PMN是等腰三角形，
∵PM∥CD1，
∴∠D2PM＝∠D2CD1，
∵PN∥BD2，
∴∠PNC＝∠D2BC，
∵∠D2PN＝∠D2CB+∠PNC＝∠D2CB+∠D2BC，
∴∠MPN＝∠D2PM+∠D2PN＝∠D2CD1+∠D2CB+∠D2BC＝∠BCD1+∠D2BC＝∠ACB+∠ACD1+∠D2BC＝∠ACB+∠ABD2+∠D2BC＝∠ACB+∠ABC，
∵∠BAC＝90°，
∴∠ACB+∠ABC＝90°，
∴∠MPN＝90°．
∴△PMN为等腰直角三角形．
∴S△PMN＝PM2＝（CD1）2＝（BD2）2，
∴当BD2取最大时，△PMN的面积最大，
此时最大面积S＝[（）]2＝．
当BD2取最小时，△PMN面积最小，
此时最小面积S＝[（）]2＝．
10．解：（1）等腰直角三角形，理由如下：
连接EG并延长交AC于K，

∵DE⊥BC，∠ACB＝90°，
∴DE∥AC，
∴∠EDG＝∠KCG，
又∵G为CD中点，
∴DG＝CG，
在△DGE与△CGK中，
，
∴△DGE≌△CGK（ASA），
∴EG＝GK，
又∵F为AE的中点，EF＝AF，
∴FG∥AC∥DE，
∴∠EFG＝∠DEF，
又∵F，H分别为AE，AC的中点，
∴HF∥EC，
∴∠AFH＝∠AEC，∠AHF＝∠ACE＝90°，
∵∠GFH＝180°﹣（∠EFG+∥AFH），∠EFG+∠AFH＝∠DEF+∠AEC＝90°，
∴∠GFH＝180°﹣90°＝90°，
又∵G，H分别为CD，AC的中点，
∴GH∥AD，
∴∠GHC＝∠DAC＝45°，
∵∠FHG＝180°﹣∠GHC﹣∠AHF＝180°﹣45°﹣90°＝45°，
∴△FGH为等腰直角三角形，
故答案为：等腰直角三角形；
（2）形状不变，理由如下
连接CE并延长交AB于点P，交AD的延长线于点O，

由图①可知∠DBE＝45°＝∠ABC，∠DEB＝90°＝∠ACB，
∴∠DBA+∠ABE＝∠ABE+∠EBC，
∴∠ABD＝∠CBE，
∵，，
∴，
∴△ABD∽△CBE，
∴，∠BCE＝∠BAD，
∵∠BPC＝∠APO，
∴∠AQC＝∠ABC＝45°，
∵点F，G，H分别为AE，CD，AC的中点，
∴FH，
∴∠AHF＝∠ACO，∠GHC＝∠CAQ，
∴△FGH为等腰直角三角形；
（3）当△BDE绕点B在平面内自由旋转时，作出E点轨迹如图所示，

∵△GFH的周长为GF，FH，GH的和，
由（2）知△GFH恒为等腰直角三角形，
∴C，
又∵F，H分别为AE，AC中点，
∴FH＝，
当E在圆B上运动时，
CE的最大值＝CB+BE，CE的最小值＝CB﹣BE，
∵CB＝6，CE＝2，
∴CE的最大值＝8，最小值＝4，
∴△FGH周长的最大值为8+4，最小值为4+2，
故4+2≤C△FGH．
11．解：（1）∵AB＝AC，DE是△ABC的中位线，
∴AD＝AE，
∴BD＝CE，
即，
如下图，过点D作DF⊥BC于点F，则DF＝MN，

∵AB＝AC，∠BAC＝90°，
∴∠B＝45°，
∴△BDF是等腰直角三角形，
∴BD＝DF，
∴BD＝MN，
即，
故答案为：1，；
（2）BD＝CE，BD＝MN，
证明：∵∠DAE＝∠BAC，
∴∠DAE﹣∠BAE＝∠BAC﹣∠BAE，
即∠BAD＝∠CAE，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS），
∴BD＝CE，
由旋转的性质知，∠DAB＝∠MAN＝α，
∵DE是△ABC的中位线，AN⊥BC，
∴△ADE∽△ABC，
∴，
∴△AMN∽△ADB，
∴，
又∵△ABC是等腰直角三角形，AN⊥BC，
∴，
∴，
即BD＝MN；
（3）①当点E在AB上时，BE＝AB﹣AE＝3，

∵∠CAE＝90°，
∴CE＝＝3，
同理（2）可证△ADB≌△AEC，
∴∠BAD＝∠ECA，
∵∠FEB＝∠AEC，
∴△FEB∽△AEC，
∴，
∴，
∴FB＝；
②当点E在BA的延长线上时，BE＝AB+AE＝9，

∵∠CAE＝90°，
∴CE＝＝3，
同理（2）可证△ADB≌△AEC，
∴∠BAD＝∠ECA，
∵∠FEB＝∠AEC，
∴△FEB∽△AEC，
∴，
∴，
∴FB＝；
综上，FB的长为或．
12．解：（一）发现探究：∵四边形ABCD是矩形，
∴∠B＝90°，
∴tan∠ACB＝＝，
∴∠ACB＝60°，
∴∠CAB＝30°，
∵四边形AEFG是矩形，
∴∠AEF＝90°，
∴AE＝AF•cos30°＝AF，AB＝AC•cos30°＝AC，
∴BE＝AB﹣AE＝（AC﹣AF）＝CF，
故答案为：BE＝CF，30°；

（二）拓展探究：结论不变．
理由：如图2中，延长CF交BE的延长线于点M，设AC交BM于点J．

∵∠CAB＝∠FAE＝30°，
∴∠BAE＝∠CAF，
∵＝＝，
∴△EAB∽△FAC，
∴＝＝，∠ABE＝∠ACF，
∵∠AJB＝∠CJM，
∴∠M＝∠JAB＝30°，
∴（1）中结论成立；

（三）问题解决：如图3中，延长FG到T，使得GT＝GF，连接CT，AT．

在Rt△ABC中，BC＝4，∠CAB＝30°，
∴AC＝2BC＝8，AB＝BC＝12，
∵AE＝AB，
∴AE＝6，
∴FG＝AE＝GT＝6，AG＝＝2，
∴AT＝＝＝4，
∴AC﹣AT≤CT≤AC+AT，
∴4≤CT≤12，
∵FG＝GT，FM＝MC，
∴GM＝CT，
∴2≤GM≤6．
13．解：（1）AC＝CF+BF，理由如下：
∵∠ACB＝90°，点E为边AB的中点，
∴AE＝CE，
∴∠ACE＝∠A＝30°，
由翻转的性质得，∠A'CE＝∠ACE，
∴∠BCF＝90°﹣30°×2＝30°，
∵BF∥AC，
∴∠CBF＝180°﹣∠ACB＝90°，
∴CF＝2BF，BC＝BF÷tan30°＝BF÷＝BF，
又∵AC＝BC÷tan30°＝BF÷＝3BF，
∴AC＝CF+BF；
（2）AC＝CF﹣BF；证明如下：
连接A'B，

由翻折的性质得，A'E＝AE，A'C＝AC，∠A＝∠CA'E，
∵点E为边AB的中点，
∴AE＝BE，
∴BE＝A'E，
∴∠EA'B＝∠EBA'，
∵BF∥AC，
∴∠A+∠ABF＝180°，
∵∠CA'E+∠EA'F＝180°，
∴∠ABF＝∠EA'F，
∵∠FA'B＝∠EA'F﹣∠EA'B，∠FBA'＝∠ABF﹣∠EBA'，
即∠FA'B＝∠FBA'，
∴A'F＝BF，
∵A'C＝CF﹣A'F，
∴AC＝CF﹣BF；
（3）连接A'B，过点F作FG⊥BC于G，
∵BF∥AC，∠ACB＝120°，
∴∠CBF＝180°﹣120°＝60°，
∴BG＝BF•cos60°＝6×＝3，FG＝BF•sin60°＝6×＝3，
∴CG＝BC﹣BG＝4﹣3＝1，
在Rt△CGF中，CF＝＝＝2，
∴AC＝BF+CF＝6+2．
14．解：（1）延长BD交PC于Q，

∵α＝60°，
∴AB＝AC，AD＝AP，
∵∠CAB＝60°＝∠PAD，
∴∠CAB+∠DAC＝∠PAD+∠DAC，
即∠DAB＝∠PAC，
∴在△CPA和△BDA中，
，
∴△CPA≌△BDA（SAS），
∴BD＝CP，
即，
在△CMQ和△AMB中，∠PCA＝∠DBA且∠QMC＝∠BMA，
∴∠CQM＝∠CAB＝60°，
故答案为：1，60°；
（2）∵线段AP绕P点逆时针旋转90°得到线段DP，
∴△PAD是等腰直角三角形，
∴∠APD＝90°，∠PAD＝∠PDA＝45°，
∴＝cos∠PAD＝cos45°＝，
∵CA＝CB，∠ACB＝90°，
∴∠CAB＝∠CBA＝45°，
∴＝cos∠CAB＝cos45°＝，
∴，
又∵∠PAD+∠CAD＝∠CAB+∠CAD，
即∠PAC＝∠DAB，
∴△PAC∽△DAB，
∴∠PCA＝∠DBA，，
即＝，
∵∠BMC＝∠CNM+∠PCA＝∠BAC+∠DBA，∠DBA＝∠PCA，
∴∠CNM＝∠BAC＝45°；
（3）设AP＝PD＝x，则AD＝x，
∵DA＝DC，
∴PC＝PD+CD＝（+1）x，
由（2）知，
∴BD＝PC＝（+1）x＝（2+）x，
∵DA＝DC，
∴∠DCA＝∠DAC，
∵∠PCA＝∠DBA，
∴∠DAC＝∠BAD，
又∵∠ADM＝∠BDA，
∴△ADM∽△BDA，
∴＝，
即AD2＝DM•BD，
∴（x）2＝（2﹣）（2+）x，
解得x＝1或x＝0（舍去），
∴AP＝1．
15．解（1）∵CD是∠ACB的平分线，∠ACB＝90°，
∴∠DCB＝45°，
∵∠DCE＝90°，
∴∠ECF＝45°，
∴∠DCF＝∠ECF，
∵CD＝CE，
∴DF＝EF，CF⊥DE，
∴BD＝BE，
故答案为：①BD＝BE；②BC⊥DE；
（2）（1）中的结论仍然成立．理由：
∵AB＝BC，点D是AB的中点，
∴∠ACD＝∠BCD＝α，
∵∠DCE＝α，
∴∠DCB＝ECB＝α，
∴∠BCD＝∠BCE，
在△DCB和△ECB中，
，
∴△DCB≌△ECB（SAS），
∴BD＝BE，
∵CD＝CE，
∴BC⊥DE；
（3）①如图3，当△AGF≌△ADE时，

在△ABC中，AB＝AC，∠BAC＝60°，
∴△ABC是等边三角形，
∴∠ACB＝∠B＝60°，
∵CD平分∠ACB，
∴∠ACE＝30°，CD⊥AB，
∵将CE绕点C顺时针旋转60°到CF，
∴AC垂直平分EF，
∴AE＝AF，EF＝2FG，
∴∠EAG＝∠FAG，
∵△AGF≌△ADE，
∴∠DAE＝∠FAG＝∠GAE＝30°，DE＝GF，
∵AD＝1，
∴DE＝AD•tan30°＝，
∴EF＝2GF＝2DE＝；
②如图4，当△AGF≌△ADE时，

由①知，AD＝GF，AD⊥CD，AC⊥EF，∠DCG＝∠FCG，
∴∠ADC＝∠FGC＝90°，
∴△CDA≌△CGF（AAS），
∴CF＝AC＝2，
∵将CE绕点C顺时针旋转60°到CF，
∴CE＝CF，∠ECF＝60°，
∴△ECF是等边三角形，
∴EF＝CF＝2；
③如图5，当△AGF≌△ADE时，

由①知，CE＝CF，∠ECG＝∠FCG＝30°，CGEF，EF＝2FG，
∵∠GAF＝∠BAC＝60°，
∴∠AFG＝30°，
∵△△AGF≌△ADE，
∴AG＝AD＝1，
∴FG＝＝，
∴EF＝2GF＝2，
综上所述，EF的长为或2或．
16．解：（1）如图①中，

∵△ABC折叠，使点B与点C重合，折痕为MN，
∴MN垂直平分线段BC，
∴CN＝BN，
∵∠MNB＝∠ACB＝90°，
∴MN∥AC，
∵CN＝BN，
∴AM＝BM．
故答案为AM＝BM．

（2）如图②中，

∵CA＝CB＝6，
∴∠A＝∠B，
由题意MN垂直平分线段BC，
∴BM＝CM，
∴∠B＝∠MCB，
∴∠BCM＝∠A，
∵∠B＝∠B，
∴△BCM∽△BAC，
∴＝，
∴＝，
∴BM＝，
∴AM＝AB﹣BM＝10﹣＝，
∴＝＝．

（3）①如图③中，

由折叠的性质可知，CB＝CB′＝6，∠BCM＝∠ACM，
∵∠ACB＝2∠A，
∴∠BCM＝∠A，
∵∠B＝∠B，
∴△BCM∽△BAC，
∴＝＝，
∴＝，
∴BM＝4，
∴AM＝CM＝5，
∴＝，
∴AC＝．

②如图③﹣1中，设PB′＝x．

∵AC＝，BC＝CB′＝6，
∴AB′＝﹣6＝，
∴AP＝AP′＝+x，
∵∠A＝∠A′＝∠MCF，∠PFA′＝∠MFC，PA＝PA′，
∴△PFA′∽△MFC，
∴＝，
∵CM＝5，
∴＝＝+，
∵OA＝OC＝，
∴0≤x≤，
∴≤≤．
17．解：（1）∵∠BAC+∠ACB＝90°，∠ABC+∠ACB+∠BAC＝180°，
∴，
∴∠ABC＝∠ACB，
∴AB＝AC，
∵OA⊥BC，
∴OB＝OC＝，
∴C（﹣3，0）；
（2）如图1，

作点D关于BCD对称点D′，连接CD′，BD′，延长DB至F，在BA上截取BP′＝BD，
∴CD′＝CD，BD′＝BD，
∴∠DD′C＝∠ADC，
∵∠ADC﹣∠CAD＝2∠ADP，
∴∠DD′C﹣∠CAD＝2∠ADP，
∴∠ACD′＝2∠ADP，
由（1）得：AO垂直平分BC，
∴∠ABD′＝2∠ADP，
∵BD＝BD′，BP′＝BD，
∴∠BDD′＝∠BD′D，∠BDP′＝∠BP′D，
∵∠FBD′＝∠BDD′+∠BD′D＝2∠BDD′，
同理可得：∠FBA＝2∠BDP′，
∴∠FBD′﹣∠FBA＝2（∠BDD′﹣∠BDP′）＝2∠ADP′，
∴∠ABD′＝2∠ADP′，
∴∠ADP＝∠ADP′，
∴点P′和点P重合，
∴CD＝BP＝2t，
∴CE＝CD＝2t，
∴E（3﹣2t，0）；
（3）如图2，

作PH∥AG，交BC于G，
∴∠PHF＝∠GCF，∠FPH＝∠CGF，∠ACB＝∠PHB，
∵∠ACB＝∠ABC，
∴∠PHB＝∠ABC，
∴PH＝PB＝2t，
∵PG＝2PF，
∴∠PF＝GF，
∴△PFH≌△GFC（AAS），
∴CG＝PH＝2t，
∵CD＝PB，
∴CD＝CG，
∴∠CDG＝∠CGD，
∴∠DCG＝180°﹣2∠CDG，
同理可得：∠ECD＝180°﹣∠CDE，
∴∠DCE+∠DCG＝360°﹣2（∠CDG+∠CDE）＝360°﹣2×120＝120°，
∴∠ECG＝120°，
∴∠ACB＝180°﹣∠ECG＝60°，
∵AB＝AC，
∴△ABC是等边三角形，
∴AB＝BC＝6，
∴PB＝AC﹣AP＝6﹣1＝5，
∴t＝．
18．解：（1）∵△ABC为等边三角形，AD⊥BC，
∴∠DAC＝30°，
∵△AEF是等边三角形，
∴∠AEF＝60°，
∴∠AGE＝90°，
在Rt△CEG中，N是EC的中点，
∴GN＝EC，
∵AB＝4，
∴BD＝CD＝2，AD＝2，
∵AE＝，
∴DE＝，
∴EC＝，
∴NG＝；
（2）∠DNM＝120°是定值，理由如下：
连接CF，BE，BE交AC于H，DN交AC于G，
∵AB＝AC，∠BAE＝∠CAF＝60°+∠CAE，AE＝AF，
∴△ABE≌△ACF（SAS），
∴∠ABE＝∠ACF，
∵M是EF的中点，N是EC的中点，
∴MN∥CF，
∴∠DGC＝∠BHC，
∵D是BC的中点，
∴BE∥DN，
∴∠ENM＝∠ECF，
∵∠BHC＝∠ABE+∠BAH＝∠ABE+60°，
∴∠DGC＝∠ABE+60°＝∠ACF+60°，
∵∠DGC＝∠DNC+∠GCN＝∠DNC+∠ACF﹣∠ECF，
∴∠DNC＝60°+∠ECF＝60°+∠ENM，
∴∠DGE＝180°﹣∠DNC＝120°﹣∠ENM，
∴∠DNM＝∠DNE+∠ENM＝120°；
（3）取AC的中点P，
∵BP+PN≥BN，
∴当B、P、N三点共线时，BN最大，
∴BN＝BP+PN＝BP+AE＝2+＝，
设BP与AD交O点，NQ⊥AD交于Q，
∵BO⊥AC，AD⊥BC，
∴BO＝BP＝×2＝，ON＝﹣＝，
∵∠BOD＝∠QON，∠BDO＝∠OQN，
∴△ONQ∽△OBD，
∴＝，
∴NQ＝，
∴S△AND＝×AD×NQ＝×2×＝，
故答案为：．


19．（1）证明：∵△CDE是等边三角形，
∴∠CDE＝∠DEC＝60°，
∵∠ACB＝90°，CA＝CB，
∴∠ACD＝∠ACB﹣∠DCE＝90°﹣60°＝30°，∠A＝∠B＝45du3，
∴∠BDE＝∠DEC﹣∠B＝60°﹣45°＝15°，
∴∠ACD＝2∠BDE；
（2）证明：由（1）得：∠ACD＝30°，
∴∠DCF＝∠ACD＝30°，
∵△CDE是等边三角形，
∴CD＝CE，∠DCE＝60°，
∴∠ECF＝∠DCE﹣∠DCF＝60°﹣30°＝30°，
∴∠DCF＝∠ECF，
在△DCF和△ECF中，
，
∴△DCF≌△ECF（SAS），
∴DF＝EF，
由折叠得：AD＝DF，
∴AD＝EF；
（3）解：如图，

作DQ⊥BC于Q，作DT⊥AC于T，
∴∠DCQ＝90°，
∵DG⊥CD，
∴∠CDG＝90°，
∵∠DCE＝60°，
∴∠G＝90°﹣∠DCE＝30°，
∴DQ＝＝2+m，
∵∠DQE＝90°，∠ABC＝45°，
∴∠BDQ＝90°﹣∠ABC＝45°，
∴∠BDQ＝∠ABC，
∴BQ＝DQ＝2+m，
∴QE+BE＝2+m，
∵BE＝m，
∴QE＝2，
∵DE＝CD＝CE＝2QE＝4，
在Rt△CDT中，∠ACD＝30°，
∴DT＝，
∵∠ACD＝∠DCF＝30°，DT⊥AC，DO⊥CF，
∴DO＝DT＝2，
由折叠得：∠DCF＝∠A＝45°，
∵∠DOF＝90°，
∴同理可得：OF＝OD＝2，
∴＝＝4．
20．解：（1）AE＝CF．
理由：连接AO．如图2，
∵AB＝AC，点O为BC的中点，∠BAC＝90°，
∴∠AOC＝90°，∠EAO＝∠C＝45°，AO＝OC．
∵∠EOF＝90°，∠EOA+∠AOF＝90°，∠COF+∠AOF＝90°，
∴∠EOA＝∠FOC，
在△EOA和△FOC中，

∴△EOA≌△FOC（ASA），
∴AE＝CF．

（2）∵AE＝CF，∴BE+CF＝BE+AE＝AB＝2，即x+y＝2，
∴y与x的函数关系式：y＝2﹣x．
x的取值范围是：0≤x≤2．

（3）△OEF能构成等腰三角形．
当OE＝EF时，如图3，点E为AB中点，点F与点A重合，BE＝AE＝1，即x＝1，
当OE＝OF时，如图4，BE＝BO＝CO＝CF＝，即x＝，
当EF＝OF时，如图5，点E与点A重合，点F为AC中点，即x＝2，
综上所述：△OEF为等腰三角形时x的值为1或或2．