






七年级下册2 幂的乘方与积的乘方多媒体教学ppt课件
展开
这是一份七年级下册2 幂的乘方与积的乘方多媒体教学ppt课件,共22页。PPT课件主要包含了学习目标,情境导入,探究新知,幂的乘方,102+2+2,依据幂的意义,乘方的定义,同底数幂的乘法法则,乘法的定义,am+m++m等内容,欢迎下载使用。
1.在探索幂的乘方运算法则的过程中,进一步体会幂的意义,发展推理能力和表达能力;2.理解并会用幂的乘方的运算法则进行计算,解决实际问题;3.能熟练正用、逆用、结合使用幂的乘方的运算法则解决各种类型题.
《流浪地球》中分别出现了太阳、木星和地球. 它们可以近似地看做是球体. 木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的多少倍?
木星的半径约是地球的10倍,它的体积是地球的________倍!
太阳的半径约是地球的102倍,它的体积是地球的_________倍!
你知道(102)3等于多少吗?
=102×102×102
(依据同底数幂的乘法)
即(102)3=102×3=106
这种关于“幂的乘方”的运算,是不是都可以化为“指数的乘积”的形式呢?
尝试计算下列各式,并说明理由 .(1) (62)4 ; (2) (a2)3 ; (3) (am)2.
(102)3=102×3=106
你发现了结果的指数有什么规律吗?
根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
⑴(62)4=62×62×62×62=6( )
⑵(a2)3=a2·a2·a2=a( )
⑶(am)2=am·am=a( ) (m是正整数).
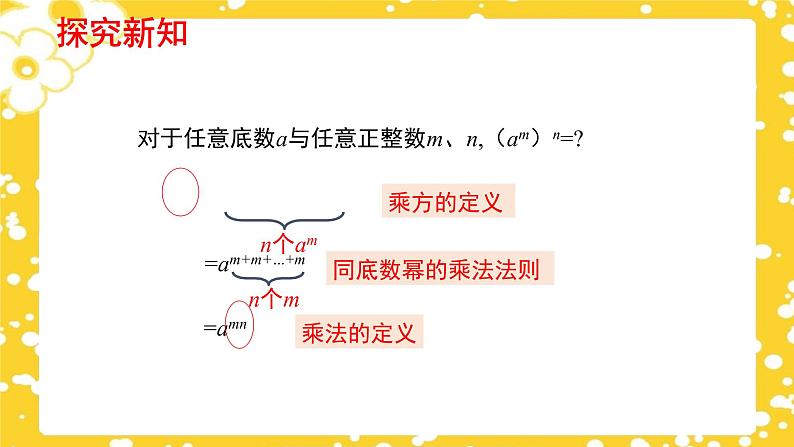
对于任意底数a与任意正整数m、n,(am)n=?
幂的乘方,底数 ,指数 .
(am)n=amn (m,n都是正整数)
注意:公式中的a可以是具体的数,也可以是单项式或多项式,当底数为多项式时,应将其视为整体。
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
例1 计算:(1) (102)3; (2) (b5) 5 ; (3) (an) 3(4) -(x2)m;(5) (y2)3 • y ; (6)2 (a2)6 - ( a3) 4
解:(1) (102)3= 102×3 = 106; (2) (b5)5 = b5×5 = b25 ; (3) (an) 3 = an×3 = a3n ; (4) -(x2)m = -x2×m = -x2m ; (5) (y2)3 • y = y2×3 • y = y7 ; (6)2 (a2)6-(a3)4=2a2×6-a3×4=2a12-a12=a12 .
注意:符号的位置和底数的确定:是底数符号还是幂的符号.
幂的乘方的逆运算:(1)x13·x7=x( )=( )5=( )4=( )10; (2)a2m =( )2 =( )m (m为正整数).
例2:如果3m+2n=6,求8m×4n的值.
8m×4n =(23)m·(22)n=23m·22n =23m+2n =26=64
分析: ①8m=(23)m=23m 4n=(22)n=22n ②式子中出现3m+2n可用6来代换 . “化为同底”好运算
在255,344,433,522这四个幂中,数值最大的一个是—————.
解:255=25×11=(25)11=3211
344=34×11=(34)11=8111
433=43×11=(43)11=6411
522=52×11=(52)11=2511
所以数值最大的一个是344.
1.计算(102)4的结果是( )A.106B.108C.109D.105
2. 下列计算正确的是( )A.a3+a3=a6 B.3a-a=3C.(a3)2=a5 D.a·a2=a3
3.下列各式中,与x5m+1相等的是( )(A)(x5)m+1 (B)(xm+1)5 (C) x · (x5)m (D) x · x5 · xm
4.x14不可以写成( )(A)x5 · (x3)3 (B) (-x) · (-x2) · (-x3) · (-x8)(C)(x7)7 (D)x3 · x4 · x5 · x2
5.⑴ a12 =(a3)( ) =(a2)( ) =a3 a( )=( )3 =( )4
(4) 32﹒9m =3( )
(2) y3n =3, y9n = .
(3) (a2)m+1 = .
6.计算:(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x6 – (x2)2· x3 .
解: (1)(103)3=109; (2)-(a2)5=-a10; (3)(x3)4 · x2 =x12·x2=x14; (4) [(-x)2 ]3=(x2)3=x6; (5)(-a)2(a2)2=a2· a4=a6; (6)x·x6 – (x2)2· x3=x7-x4·x3=0
7.计算(1)(a3)4; (2)(xm-1)2; (3)[(24)3]3; (4)[(m-n)3]4.
解:(1)(a3)4=a3×4=a12;(2)(xm-1)2=x2(m-1)=x2m-2;(3)[(24)3]3=24×3×3=236;(4)[(m-n)3]4=(m-n)12.
8. 已知 am=2,an=3, 求:(1)a2m ,a3n的值;
=(am)2. (an)3
(3)a2m+3n 的值.
(2)am+n 的值;
相关课件
这是一份初中2 幂的乘方与积的乘方优秀课件ppt,共25页。PPT课件主要包含了学习目标,情境导入,幂的乘方,102+2+2,依据幂的意义,探究新知,乘方的定义,同底数幂的乘法法则,乘法的定义,am+m++m等内容,欢迎下载使用。
这是一份北师大版七年级下册2 幂的乘方与积的乘方备课ppt课件,文件包含121幂的乘方与积的乘方pptx、12幂的乘方与积的乘方第1课时幂的乘方doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
这是一份初中数学北师大版七年级下册2 幂的乘方与积的乘方精品ppt课件,共26页。PPT课件主要包含了理解算理,发现规律,数学公式,不是幂的乘方,102+2+2,乘方的意义,102×3,乘法的意义,amn,amnamn等内容,欢迎下载使用。









