

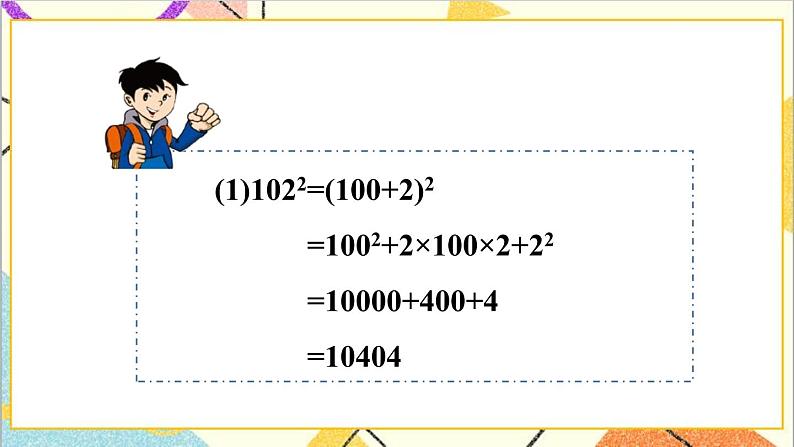







- 1.5.2 平方差公式的应用 课件+教案 课件 7 次下载
- 1.6.1 完全平方公式的认识 课件+教案 课件 10 次下载
- 1.7.1 单项式除以单项式 课件+教案 课件 10 次下载
- 1.7.2 多项式除以单项式 课件+教案 课件 9 次下载
- 第一章 整式的乘除 章末复习 课件+教案 课件 14 次下载
数学北师大版6 完全平方公式一等奖课件ppt
展开前面我们学习了完全平方公式:
想一想,怎样计算1022,1972更简单呢?
(1)(x+3)2-x2;
解:(x+3)2-x2 =x2+6x+9-x2 =6x+9
(2)(a+b+3) (a+b-3);
解:(a+b+3) (a+b-3) =[(a+b)+3][(a+b)-3] =(a+b)2-32 =a2+2ab+b2-9
(3)(x+5)2-(x-2)(x-3).
解:(x+5)2-(x-2)(x-3) =x2+10x+25-(x2-5x+6) =x2+10x+25-x2+5x-6 =15x+19
一位老人非常喜欢孩子.每当有孩子到他家做客时,老人都要拿出糖果招待他们.如果来1个孩子,老人就给这个孩子1块糖果; 来2个孩子,老人就给每个孩子2块糖果;如果来3个孩子,老人就给每个孩子3块糖果……
假如第一天有a个孩子一起去看老人,第二天有b个孩子一起去看老人,第三天有(a+b)个孩子一起去看老人,那么第三天老人给出去的糖果和前两天给出去的糖果总数一样多吗? 请你用所学的公式解释自己的结论.
第一天a个孩子,给出去的糖果a×a=a2.
第二天b个孩子,给出去的糖果b×b=b2.
第二天(a+b)个孩子,给出去的糖果(a+b)2=a2+2ab+b2.
所以第三天老人给出去的糖果比前两天给出去的糖果多.
1.若m+n=3,则代数式2m2+4mn+2n2-6的值为( )
2.若(a+b)2=49,ab=6,则a-b的值为( )A.-5B.±5C.5D.±4
3.已知a=2002x+2003,b=2002x+2004,c=2002x+2005,则多项式2a2+2b2+2c2-2ab-2bc-2ac的值为( )
4.利用整式乘法公式计算:
(2)(a-b-3) (a-b+3)
解:962 =(100-4)2 =1002-2×100×4+42 =10000-800+16 =9216
解:(a-b-3) (a-b+3) =(a-b)2-32 =a2-2ab+b2-9
(1)(2x+y+1) (2x+y-1)
解:(2x+y+1) (2x+y-1) =(2x+y)2-12 =4x2+4xy+y2-1
(2)(x-2)(x+2)-(x+1)(x-3)
解:(x-2)(x+2)-(x+1)(x-3) =x2-4-(x2-2x-3) =2x-1
(3)(ab+1)2-(ab-1)2
解:(ab+1)2-(ab-1)2 =4ab
(4)(2x-y)2-4(x-y)(x+2y)
解:(2x-y)2-4(x-y)(x+2y) =9y2-8xy
6. 一个底面是正方形的长方体,高为6cm,底面正方形边长为5cm.如果它的高不变,底面正方形边长增加acm,那么它的体积增加了多少?
解:6×(5+a)2-6×52 =6×(a+5+5)(a+5-5) =6×(a2+10) =6a2+60
利用完全平方公式简便计算
北师大版七年级下册6 完全平方公式教学课件ppt: 这是一份北师大版七年级下册6 完全平方公式教学课件ppt,文件包含162完全平方公式pptx、16完全平方公式第2课时完全平方公式的应用doc等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
初中6 完全平方公式精品ppt课件: 这是一份初中6 完全平方公式精品ppt课件,共21页。PPT课件主要包含了完全平方公式,知识回顾,公式特征,积为二次三项式,15x+19,a+b2,课堂小结,常用结论,=36-16=20,=20-16=4等内容,欢迎下载使用。
初中数学北师大版七年级下册6 完全平方公式评课ppt课件: 这是一份初中数学北师大版七年级下册6 完全平方公式评课ppt课件,共24页。PPT课件主要包含了学习目标,情境导入,×49,探究新知,完全平方公式的运用,利用平方差公式计算,100+2,100+22,200-3,200-32等内容,欢迎下载使用。













