4.3.3利用“边角边”判定三角形全等 课件+教案

第3课时  利用“边角边”判定三角形全等

【知识与技能】

1.能主动积极探索出三角形全等的条件“SAS”.

2.能熟练运用“SAS”判别方法来进行有条理的思考并进行简单的证明.

3.初步综合运用四种判别方法来判别三角形全等.

【过程与方法】

学生经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程，由此带动知识发生、发展的全过程.

【情感态度】

通过多种手段的活动过程，让学生动手操作，激发学生学习的兴趣，并能通过合作交流解决问题，体会数学在现实生活中的应用，增强学生的自信心.

【教学重点】

掌握三角形全等的条件“SAS”，并能利用它来判定三角形是否全等.

【教学难点】

探索三角形全等的条件“SAS”的过程及几种方法的综合应用.

一、情景导入，初步认知

我们已学过判定两个三角形全等的哪些条件?

我们还没有研究三个条件的哪一种情况?

【教学说明】引导学生积极的回顾旧知，利于将知识连贯起来.

二、思考探究，获取新知

探究：如果给出一个三角形的“两边一角”能确定这个三角形吗？

1.请同学们想一想，已知三角形的两条边和一个角时会有几种不同的基本情况?

2.操作并研讨.

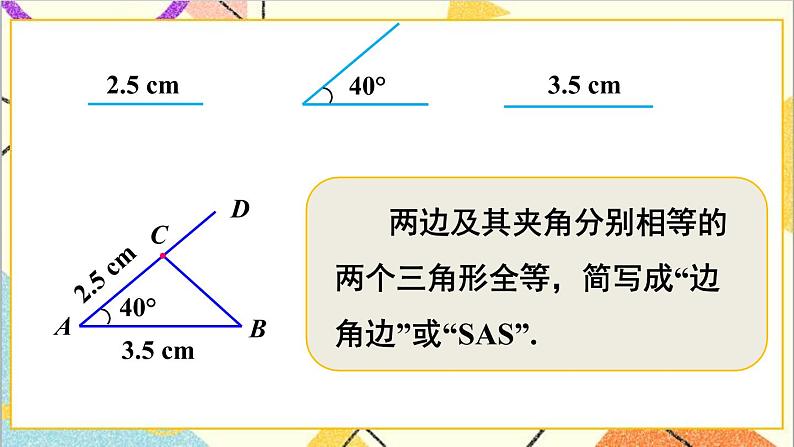
（1）让学生画一个三角形，使它满足两条边长分别为2cm和3cm，且它们的夹角为40°.画完后用剪刀剪下来，和其他同学剪的三角形比较，看看是否能够重合.

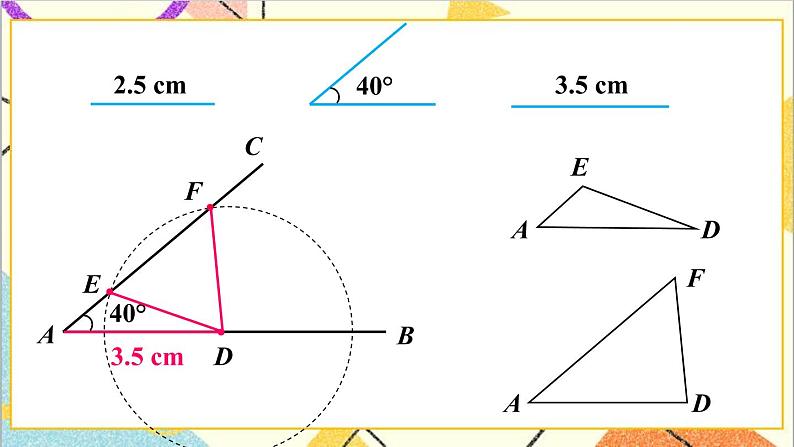
（2）让学生画一个三角形，使它满足两条边长分别为2cm和3cm，且其中一条边的对角是40°.

（3）满足条件的三角形出现了两种形状完全不同的三角形

3.由此，你能得出什么结论？

【归纳结论】

两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”.

【教学说明】

学生通过画图、观察、比较，终于明白为什么两条边及一边的对角这三个条件不能确定三角形的形状和大小的道理.

三、运用新知，深化理解

1.如图，在△ABC和△DEF中，已知AB=DE，BC=EF，根据（SAS）判定△ABC≌△DEF，还需的条件是（ B ）

A.∠A=∠D     B.∠B=∠E     C.∠C=∠F     D.以上三个均可以

2.如图，AD=AE，BE=CD，∠1=∠2=110°,∠BAE=60°,则∠CAE= 20°.

3.如图，已知AC⊥BD，BC=CE,AC=DC，则∠B与∠D的关系是互余.

4.如图，AC=AD，AB平分∠CAD，那么BC=BD吗?为什么?

解：BC=BD，理由是：

AB平分∠CAD，

∠CAB=∠DAB.

在△ABC和△ABD中，

AC＝AD,

∠CAB＝∠DAB,

AB＝AB,

△ABC≌△ABD（SAS）,

BC＝BD.

5.如图,AD∥CB，AD＝CB，那么∠B=∠D吗?为什么?

解：∠B=∠D，理由是：

AD∥CB,

∠DAC＝∠BCA.

在△ABC和△CDA中，

BC=AD,

∠BCA＝∠DAC,

AC＝CA,

ABC≌△CDA（SAS）,

∠B＝∠D.

6.如图，已知在△ABC中，AB=AC，∠1=∠2.试判断AD与BC，BD与DC的关系并说明理由.

解：在△ABD和△ACD中，

∵AB=AC（已知）

∠1=∠2（已知）

AD=AD（公共边）

∴△ABD≌△ACD（SAS）.

∴BD=CD，∠3=∠4.

又∵∠3+∠4=180°，即2∠3=180°，

∴∠3=90°，∴AD⊥BC.

【教学说明】检验学生的掌握情况,培养学生的逻辑思维能力.

四、师生互动,课堂小结

先小组内交流收获和感想，而后以小组为单位派代表进行总结.教师作以补充.

五、教学板书

1.布置作业:教材“习题4.8”中第1、2题.

2.完成同步练习册中本课时的练习.

本节在应用定理判定三角形全等时的练习有点多，可能有些学生思维有点跟不上，是本节课的一大遗憾.另外，在小组交流时气氛不是很活跃.最后，我考虑在这种情况下是否可以让一个小组展示，一个小组讲解可能会更好一些.

总之，从本节课的教学效果来看，学生能达到这个程度还算可以，实现了本节课的教学目标.自己以后要吸取教训.