


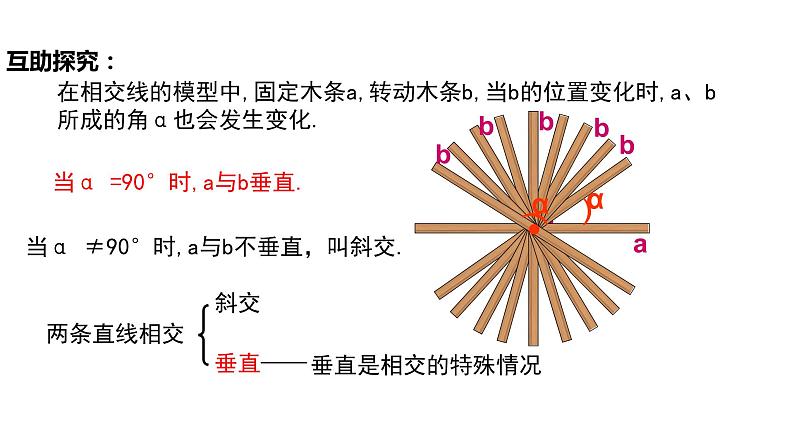

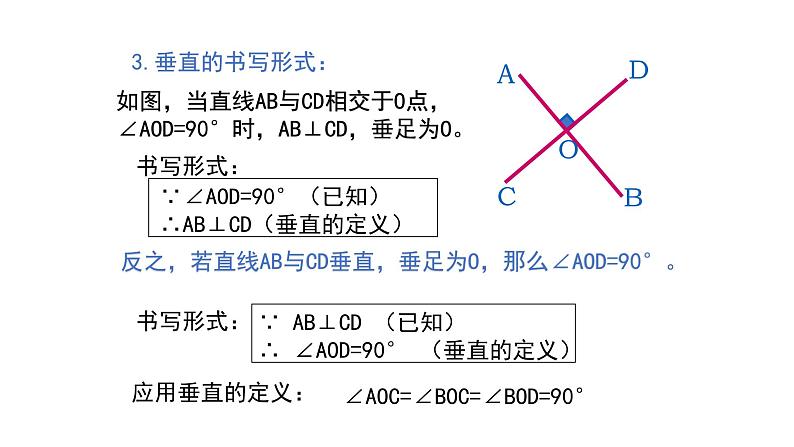
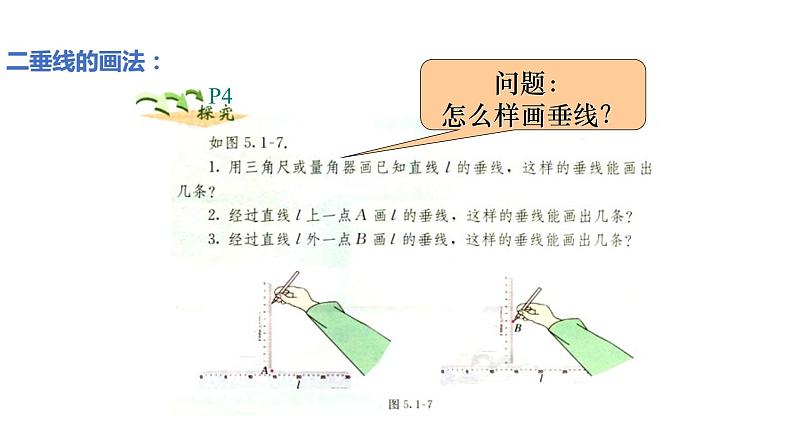
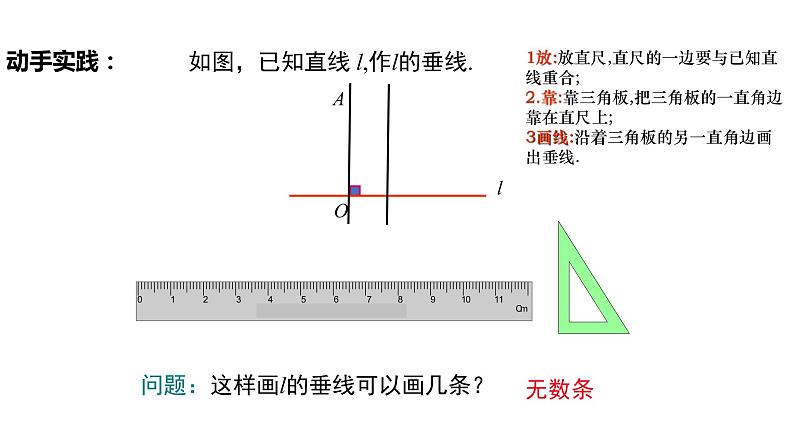





- 5.1.1 相交线(导学案+课件+作业)-2022-2023学年七年级数学下册同步精品课件(人教版) 课件 1 次下载
- 5.1.3 同位角、内错角、同旁内角(导学案+课件+作业)-2022-2023学年七年级数学下册同步精品课件(人教版) 课件 1 次下载
- 5.2.2 平行线的判定(导学案+课件+作业)-2022-2023学年七年级数学下册同步精品课件(人教版) 课件 1 次下载
- 5.3.1 平行线的性质(导学案+课件+作业)-2022-2023学年七年级数学下册同步精品课件(人教版) 课件 1 次下载
- 5.3.2 命题、定理、证明(导学案+课件+作业)-2022-2023学年七年级数学下册同步精品课件(人教版) 课件 1 次下载
初中数学人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.2 垂线完整版作业课件ppt
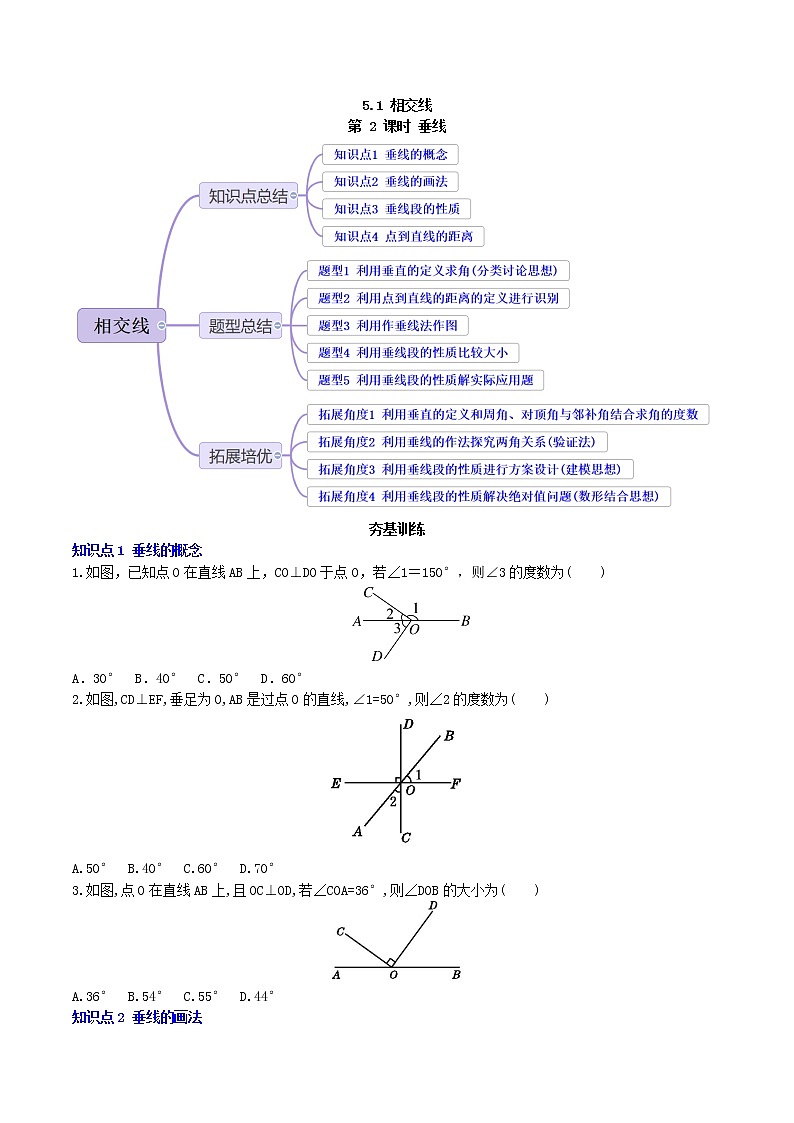
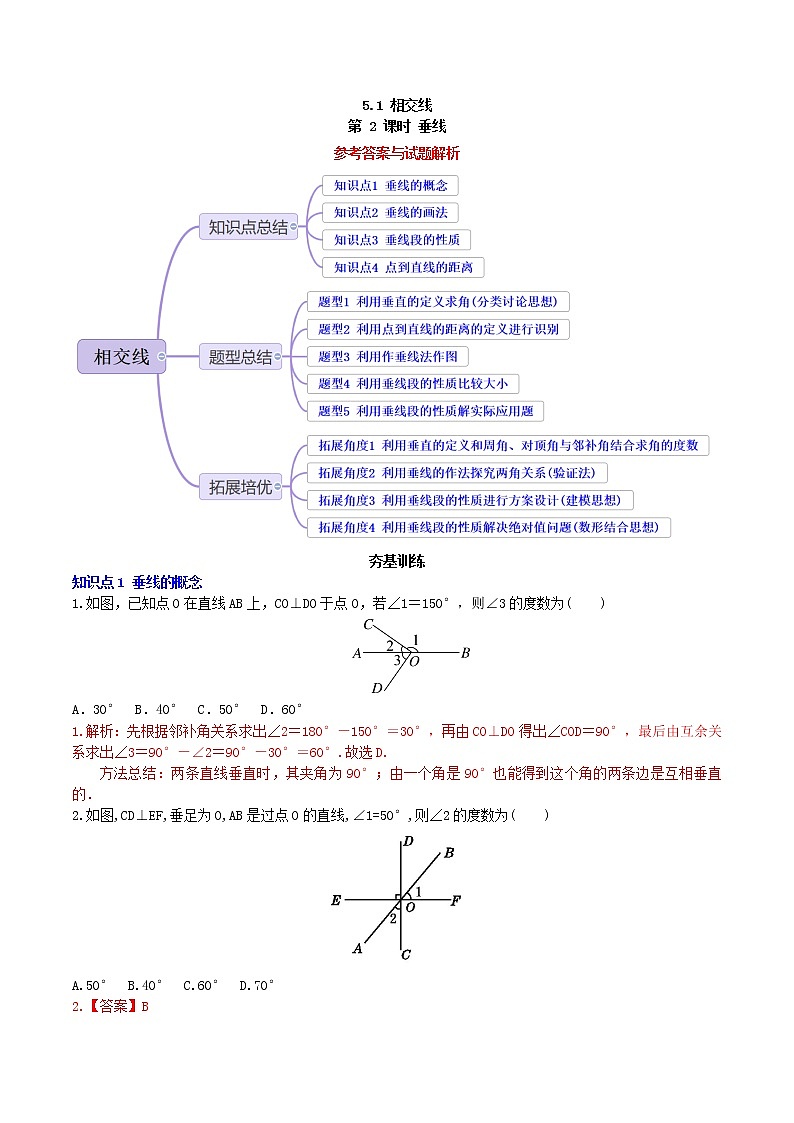
展开5.1 相交线
第 2 课时 垂线
参考答案与试题解析
夯基训练
知识点1 垂线的概念
1.如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=150°,则∠3的度数为( )
A.30° B.40° C.50° D.60°
1.解析:先根据邻补角关系求出∠2=180°-150°=30°,再由CO⊥DO得出∠COD=90°,最后由互余关系求出∠3=90°-∠2=90°-30°=60°.故选D.
方法总结:两条直线垂直时,其夹角为90°;由一个角是90°也能得到这个角的两条边是互相垂直的.
2.如图,CD⊥EF,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )
A.50° B.40° C.60° D.70°
2.【答案】B
解:因为CD⊥EF,所以∠DOF=90°,即∠1+∠DOB=90°,而∠1=50°,所以∠DOB=40°.又∠DOB与∠2是对顶角,所以∠2=∠DOB=40°,故选B.
3.如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36° B.54° C.55° D.44°
3.【答案】B
解:因为OC⊥OD,所以∠COD=90°,又因为∠AOC+∠COD+∠DOB=180°,所以∠DOB=180°-36°-90°=54°.故选B.
知识点2 垂线的画法
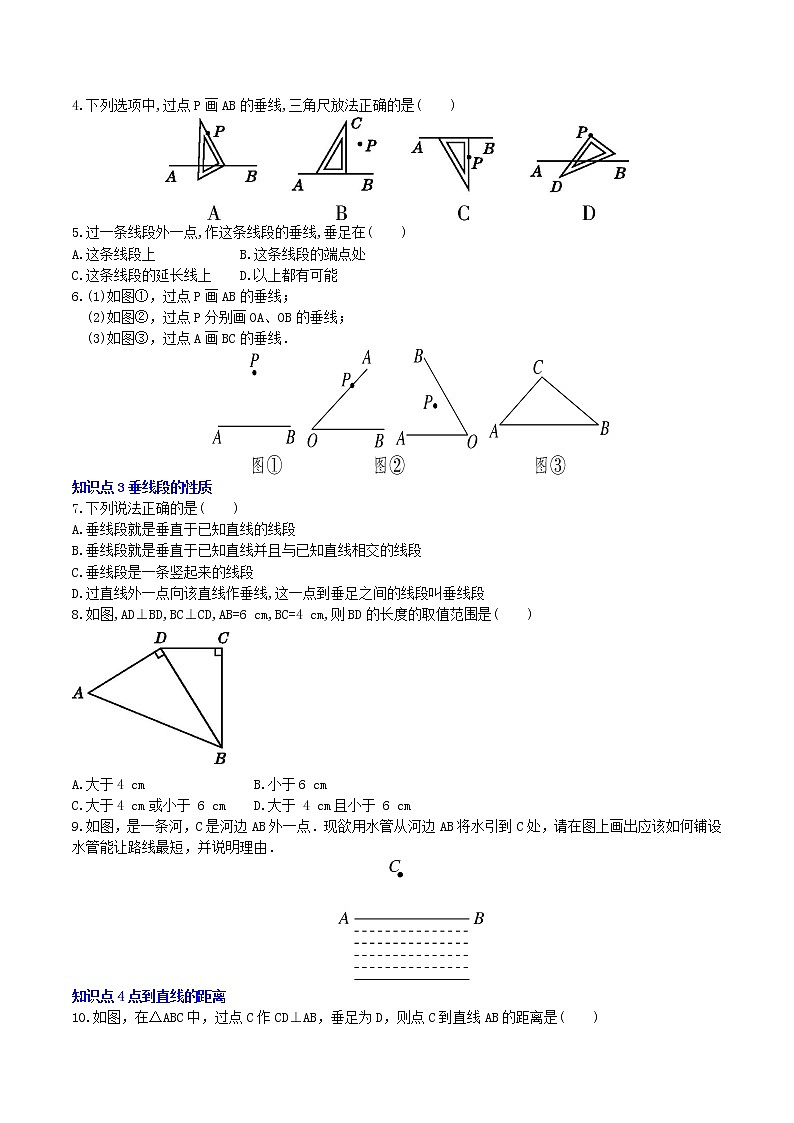
4.下列选项中,过点P画AB的垂线,三角尺放法正确的是( )
4.【答案】C
5.过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上 B.这条线段的端点处
C.这条线段的延长线上 D.以上都有可能
5.【答案】D
6.(1)如图①,过点P画AB的垂线;
(2)如图②,过点P分别画OA、OB的垂线;
(3)如图③,过点A画BC的垂线.
6.解析:分别根据垂线的定义作出相应的垂线即可.
解:如图所示.
方法总结:垂线的画法需要三步完成:一落:让三角板的一条直角边落在已知直线上,使其与已知直线重合;二移:沿直线移动三角板,使其另一直角边经过所给的点;三画:沿此直角边画直线,则这条直线就是已知直线的垂线.
知识点3垂线段的性质
7.下列说法正确的是( )
A.垂线段就是垂直于已知直线的线段
B.垂线段就是垂直于已知直线并且与已知直线相交的线段
C.垂线段是一条竖起来的线段
D.过直线外一点向该直线作垂线,这一点到垂足之间的线段叫垂线段
7.【答案】C
8.如图,AD⊥BD,BC⊥CD,AB=6 cm,BC=4 cm,则BD的长度的取值范围是( )
A.大于4 cm B.小于6 cm
C.大于4 cm或小于 6 cm D.大于 4 cm且小于 6 cm
8.【答案】D
解:根据“垂线段最短”可知BC<BD<AB,所以BD大于4 cm且小于6 cm.
9.如图,是一条河,C是河边AB外一点.现欲用水管从河边AB将水引到C处,请在图上画出应该如何铺设水管能让路线最短,并说明理由.
9.解析:根据垂线的性质可解,即过C作CE⊥AB,根据“垂线段最短”可得CE最短.
解:如图所示,沿CE铺设水管能让路线最短,因为垂线段最短.
方法总结:在利用垂线的性质解决生活中最近、最短距离的问题时,要依据“两点之间,线段最短”和“垂线段最短”来解决.
知识点4点到直线的距离
10.如图,在△ABC中,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B.线段CD
C.线段AD的长 D.线段CD的长
10.解析:根据点到直线的距离的定义:直线外一点到直线的垂线段的长度叫做点到直线的距离,可得点C到直线AB的距离是线段CD的长.故选D.
方法总结:点到直线的距离是直线外一点到直线的垂线段的长度,而不是垂线段.
11.如图,其长能表示点到直线(线段)的距离的线段的条数是( )
A.3 B.4 C.5 D.6
11.【答案】C
解:线段AB的长度可表示点B到AC的距离,线段CA的长度可表示点C到AB的距离,线段AD的长度可表示点A到BC的距离,线段CD的长度可表示点C到AD的距离,线段BD的长度可表示点B到AD的距离,所以共有5条.
题型总结
题型1 利用垂直的定义求角(分类讨论思想)
12.已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD的度数;
(2)如图②,若∠BOC=60°,求∠AOD的度数;
(3)根据(1)(2)的结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由;
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠BOC和∠AOD的度数.
12.解:(1)因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB-∠BOC=90°-50°=40°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)因为OA⊥OB,所以∠AOB=90°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=360°-∠AOB-∠BOC-∠COD=360°-90°-60°-90°=120°.
(3)∠AOD与∠BOC互补.理由如下:因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB-∠BOC=90°-∠BOC.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=90°-∠BOC+90°=180°-∠BOC,所以∠AOD+∠BOC=180°,即∠AOD与∠BOC互补(4)由(3)知∠BOC+∠AOD=180°,
又因为∠BOC∶∠AOD=7∶29,
所以∠BOC=×180°=35°,
∠AOD=×180°=145°.
题型2利用点到直线的距离的定义进行识别
13.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )
A.2条 B.3条 C.4条 D.5条
13.【答案】D
题型3利用作垂线法作图
14.如图,已知钝角三角形ABC中,∠BAC为钝角.
(1)画出点C到AB的垂线段;
(2)过点A画BC的垂线;
(3)画出点B到AC的垂线段,并量出其长度.
14.解:如图:(1)CD即为所求;(2)直线AE即为所求;(3)BF即为所求.长度略.
题型4利用垂线段的性质比较大小
15.如图,直线AB,CD相交于点O,P是CD上一点.
(1)过点P画AB的垂线段PE;
(2)过点P画CD的垂线,与AB相交于F点;
(3)说明线段PE,PO,FO三者的大小关系,其依据是什么?
15.解:(1)如图所示. (2)如图所示.
(3)PE<PO<FO,其依据是垂线段最短.
题型5利用垂线段的性质解实际应用题
16.如图,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,设汽车行驶到点P位置时,离村庄M最近,行驶到点Q位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
16.解:如图所示.
拓展培优
拓展角度1利用垂直的定义和周角、对顶角与邻补角结合求角的度数
17.如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3的度数.
17.解析:首先根据垂直的概念得到∠BOD=90°,然后根据∠1与∠3是对顶角,∠2与∠3互为余角,从而求出角的度数.
解:由题意得∠3=∠1=30°(对顶角相等).∵AB⊥CD(已知),∴∠BOD=90°,(垂直的定义),∴∠3+∠2=90°,即30°+∠2=90°,∴∠2=60°.
方法总结:解决本题的关键是根据垂直的概念,得到度数为90°的角,然后根据对顶角、邻补角的性质解决.
拓展角度2利用垂线的作法探究两角关系(验证法)
18.(1)在图①中以P为顶点作∠P,使∠P的两边分别和∠1的两边垂直;
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠P,使∠P的两边分别和∠1的两边垂直,分别写出图②和③中∠P和∠1之间的数量关系(不要求写出理由).图②: ,图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
18.解:(1)如图①所示.
(2)∠1+∠P=180°
(3)如图②③,∠1=∠P;∠1=∠APC或∠1+∠BPC=180°
(4)相等或互补
拓展角度3利用垂线段的性质进行方案设计(建模思想)
19.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水池H的位置,使它到四个村庄的距离之和最小;
(2)计划把河水引入蓄水池H中,怎样开渠最短?并说明根据.
19.解:(1)如图,连接AD,BC,交于点H,则H点为蓄水池的位置,它到四个村庄的距离之和最小.
(2)如图,过点H作HG⊥EF,垂足为G,则沿HG开渠最短.根据:连接直线外一点与直线上各点的所有线段中,垂线段最短.分析:本题考查了垂线段的性质在实际生活中的运用.体现了建模思想的运用.
拓展角度4利用垂线段的性质解决绝对值问题(数形结合思想)
20.在如图所示的直角三角形ABC中,斜边为BC,两直角边分别为AB,AC,设BC=a,AC=b,AB=c.
(1)试用所学知识说明斜边BC是最长的边;
(2)试化简|a-b|+|c-a|+|b+c-a|.
20.解:(1)因为点C与直线AB上点A,B的连线中,CA是垂线段,所以AC<BC.因为点B与直线AC上点A,C的连线中,AB是垂线段,所以AB<BC.故AB,AC,BC中,斜边BC最长.
(2)因为BC>AC,AB<BC,AC+AB>BC,所以原式=a-b-(c-a)+b+c-a=a.
人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.2 垂线精品教学ppt课件: 这是一份人教版七年级下册<a href="/sx/tb_c88515_t3/?tag_id=26" target="_blank">第五章 相交线与平行线5.1 相交线5.1.2 垂线精品教学ppt课件</a>,文件包含人教版数学七年级下册512《垂线》课件pptx、人教版数学七年级下册512《垂线》教学设计docx、人教版数学七年级下册512《垂线》导学案docx等3份课件配套教学资源,其中PPT共36页, 欢迎下载使用。
5.1.2垂线(课件)-2022-2023学年七年级数学下册同步精品课堂(人教版): 这是一份5.1.2垂线(课件)-2022-2023学年七年级数学下册同步精品课堂(人教版),共25页。PPT课件主要包含了无数条,你发现了什么,PO最短,特别规定,垂线段最短,垂线的定义,垂线的画法,垂线的性质,点到直线的距离等内容,欢迎下载使用。
初中数学人教版七年级下册5.1.2 垂线教案配套ppt课件: 这是一份初中数学人教版七年级下册5.1.2 垂线教案配套ppt课件,共27页。PPT课件主要包含了新课导入,新知探究,垂线的概念,AB⊥CD垂足为O,归纳小结,垂线的性质,巩固练习,m⊥n,垂线的画法及基本事实,点在直线上等内容,欢迎下载使用。













