高中数学人教B版 (2019)必修 第一册3.3 函数的应用(一)同步练习题

3.3 函数的应用(一)

一、概念练习

1.某商品自上市后前两年价格每年递增10%，第三年价格下降了20%，则第三年降价后与上市时价格相比，变化情况是(   )

A.不增不减 B.下降了2.8％ C.增加了2.8% D.下降了3.2％

2.某工厂第三年的产量比第一年的产量增长44%，若每年的平均增长率相同(设为x)，则下列结论中正确的是(   )

A.  B.

C.  D.x的大小由第一年产量确定

3.某种型号的手机自投放市场以来，经过两次降价，单价由原来的2000元降到1280元，则这种手机平均每次降价的百分率是(   )

A.10% B.15% C.18% D.20%

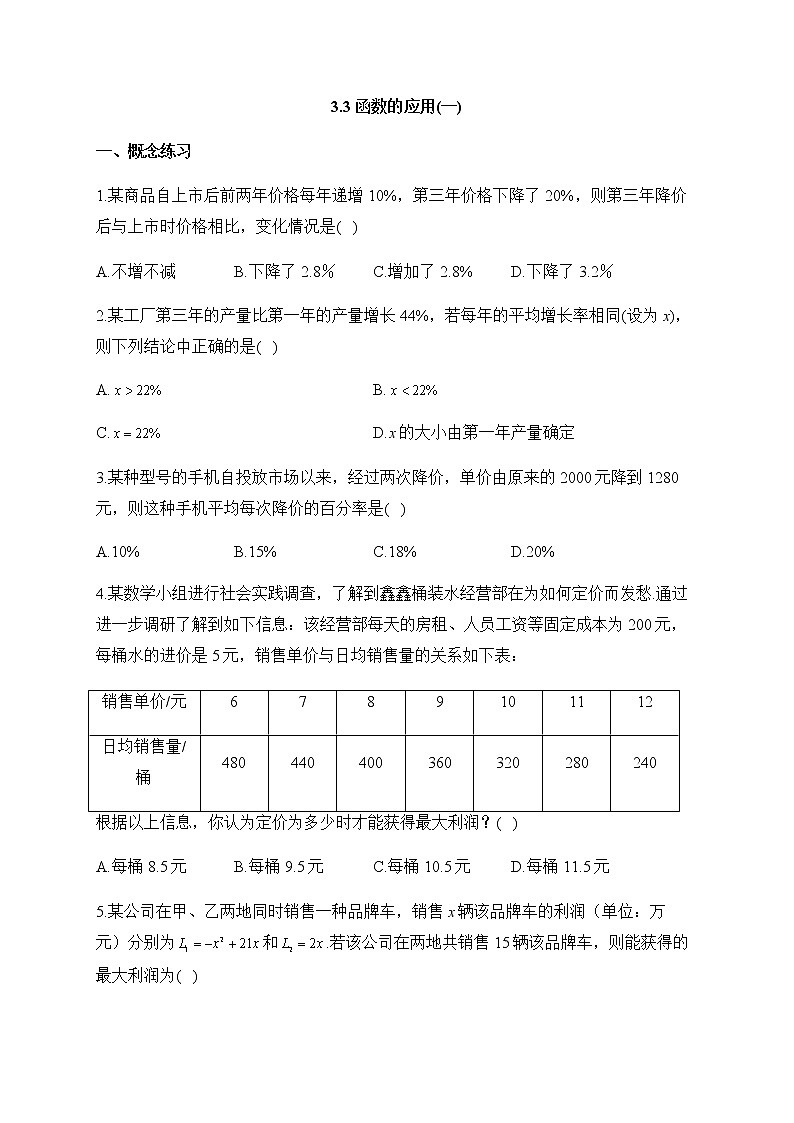
4.某数学小组进行社会实践调查，了解到鑫鑫桶装水经营部在为如何定价而发愁.通过进一步调研了解到如下信息：该经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元，销售单价与日均销售量的关系如下表：

根据以上信息，你认为定价为多少时才能获得最大利润？(   )

A.每桶8.5元 B.每桶9.5元 C.每桶10.5元 D.每桶11.5元

5.某公司在甲、乙两地同时销售一种品牌车，销售x辆该品牌车的利润（单位：万元）分别为和.若该公司在两地共销售15辆该品牌车，则能获得的最大利润为(   )

A.90万元 B.60万元 C.120万元 D.120.25万元

二、能力提升

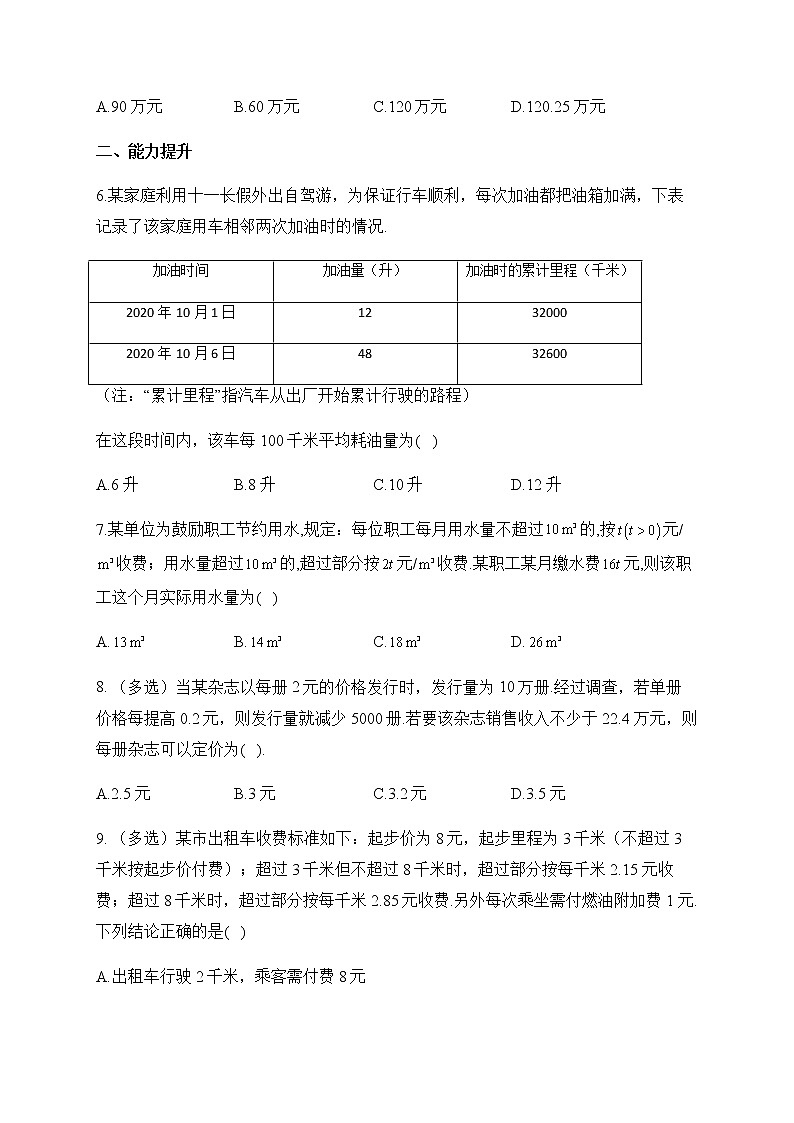
6.某家庭利用十一长假外出自驾游，为保证行车顺利，每次加油都把油箱加满，下表记录了该家庭用车相邻两次加油时的情况.

（注：“累计里程”指汽车从出厂开始累计行驶的路程）

在这段时间内，该车每100千米平均耗油量为(   )

A.6升 B.8升 C.10升 D.12升

7.某单位为鼓励职工节约用水,规定：每位职工每月用水量不超过的,按元/收费；用水量超过的,超过部分按元/收费.某职工某月缴水费元,则该职工这个月实际用水量为(   )

A. B. C. D.

8. （多选）当某杂志以每册2元的价格发行时，发行量为10万册.经过调查，若单册价格每提高0.2元，则发行量就减少5000册.若要该杂志销售收入不少于22.4万元，则每册杂志可以定价为(   ).

A.2.5元 B.3元 C.3.2元 D.3.5元

9. （多选）某市出租车收费标准如下：起步价为8元，起步里程为3千米（不超过3千米按起步价付费）；超过3千米但不超过8千米时，超过部分按每千米2.15元收费；超过8千米时，超过部分按每千米2.85元收费.另外每次乘坐需付燃油附加费1元.下列结论正确的是(   )

A.出租车行驶2千米，乘客需付费8元

B.出租车行驶4千米，乘客需付费9.6元

C.出租车行驶10千米，乘客需付费25.45元

D.某人两次乘出租车均行驶5千米的费用之和超过他一次乘出租车行驶10千米的费用

10. （多选）某部影片的盈利额(即影片的票房收入与固定成本之差)记为,观影人数记为关于的函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后关于的函数图象.

给出下列四种说法,其中正确的说法是(   )

A.图(2)对应的方案是:提高票价,并提高固定成本

B.图(2)对应的方案是:保持票价不变,并降低固定成本

C.图(3)对应的方案是:提高票价,并保持固定成本不变

D.图(3)对应的方案是:提高票价,并降低固定成本

11.某地上年度电价为0.8元/度，年用电量为1亿度.本年度计划将电价调至元/度之间（包含0.55元/度和0.75元/度），经测算，若电价调至x元/度，则本年度新增用电量y（亿度）与（）（元/度）成反比，且当时，.则y与x之间的函数关系式为________.

12.某电脑公司2019年的各项经营收入中，经营电脑配件的收人为400万元，占全年经营总收入的，该公司预计2021年经营总收入要达到1690万元，且计划从2019年到2021年，每年经营总收入的年增长率相同,则2020年预计经营总收入为___________万元.

13.某大楼共有20层，有19人在第1层上了电梯，他们分别要去第2层至第20层，每层1人，而电梯只允许停1次，可只使1人满意，其余18人都要步行上楼或下楼，假设乘客每向下走一层的不满意度为1，每向上走层的不满意度为2，所有人的不满意度之和为S，为使S最小，电梯应当停在第________层.

14.某地某路无人驾驶公交车发车时间间隔t（单位：分钟）满足，.经测算，该路无人驾驶公交车载客量与发车时间间隔t满足：其中.

（1）求，并说明的实际意义；

（2）若该路公交车每分钟的净收益（元），问当发车时间间隔为多少时，该路公交车每分钟的净收益最大？并求每分钟的最大净收益.

15.如图，有一个边长为10m的正方形小花坛ABCD，现欲在中间修建一块长方形PQMN护栏区域培植稀有植物（不考虑护栏的厚度），根据需要以QM长度的一半为半径，以A、B、C、D各顶点为圆心的四分之一圆内都种植花卉，其中P，Q，M，N四点都在相应的圆弧上，并且培植稀有植物边界与小花坛边界对应平行，假设QM的长度为x（）米，长方形PQMN护栏的周长为L.

（1）请写出用L表示含有x的函数关系式；

（2）求护栏周长L的范围.

答案以及解析

1.答案：D

解析：本题考查函数模型与生活中的应用.设商品原价格为a元，则，下降了.

2.答案：B

解析：由题意设第一年的产量为a，则第三年的产量为，解得.故选B.

3.答案：D

解析：设平均每次降价的百分率为x，则，所以，故选D.

4.答案：D

解析：通过题中表格可知销售单价每增加1元，日均销售量减少40桶，设每桶水的价格为元，日利润为y元，则，

，当时y有最大值，

每桶水的价格为11.5元时，日利润最大，故选D.

5.答案：C

解析：设公司在甲地销售m辆该品牌车，则在乙地销售辆，，且，设公司获利为L万元，

则，

当或时，L取得最大值120，即该公司在两地共销售15辆该品牌车时，能获得的最大利润为120万元.故选C.

6.答案：B

解析：由题表中的信息可知，2020年10月1日油箱加满了油，此时的累计里程为32000千米，到2020年10月6日，油箱加满油需要48升，说明这段时间的耗油量为48升，累计里程为32600千米，说明这段时间内汽车行驶了600千米，

则在这段时间内，该车每100千米平均耗油量为升.故选B.

7.答案：A

解析：该职工每月应缴水费(单位：元)与实际用水量(单位：)满足的关系式为.由,可知.令,解得.

8.答案：BC

解析：依题意可知，要使该杂志销售收入不少于22.4万元，只能提高销售价，设每册杂志定价为元，则发行量为万册，则该杂志销售收入为万元，所以，化简得，解得，故选BC.

9.答案：CD

解析：在A中，出租车行驶2千米，乘客需付起步价8元和燃油附加费1元，共9元，A错误；在B中，出租车行驶4千米，乘客需付费（元），B错误；在C中，出租车行驶10千米，乘客需付费（元），C正确；在D中，乘出租车行驶5千米，乘客需付费（元），乘坐两次需付费26.6元，，D正确.故选CD.

10.答案：BC

解析：由图(1)可设关于的函数为为票价,当时,,则为固定成本.由图(2)知,直线向上平移,不变,即票价不变,变大,则变小,固定成本减小,故A错误,B正确;由图(3)知,直线与轴的交点不变,直线斜率变大,即变大,票价提高,不变,即不变,固定成本不变,故C正确,D错误.故答案为BC.

11.答案：

解析：因为y与成反比，所以设，把，代入上式,得，解得，所以，所以y与x之间的函数关系式为.

12.答案：1300

解析：设年增长率为，则，所以，因此2020年预计经营总收入为（万元）.

13.答案：14
解析：设停在第x层，则，当时，S取最小值.，时，S取最小值.

14.答案：（1），实际意义为：发车时间间隔为5分钟时，载客量为35

（2）当发车时间间隔为6分钟时，该路公交车每分钟的净收益最大，每分钟的最大净收益为38元

解析：（1）.

实际意义为：发车时间间隔为5分钟时，载客量为35.

（2），

当，时，，当且仅当，即（负值舍去）时，等号成立，的最大值为38.

当，时，，该函数在区间上单调递减，则当时，y取得最大值28.4.

综上，当发车时间间隔为6分钟时，该路公交车每分钟的净收益最大，每分钟的最大净收益为38元.

15.答案：（1），

（2）

解析：（1）过Q作于E，连接BQ（图略），
在中，，则，
则矩形周长，.

（2）由（1）知，，
换元法：令，则，，
则.
因为其图象对称轴为，
，，所以周长L的范围为.