人教B版 (2019)2.2.4 均值不等式及其应用课时作业

这是一份人教B版 (2019)2.2.4 均值不等式及其应用课时作业，共11页。试卷主要包含了单选题等内容，欢迎下载使用。
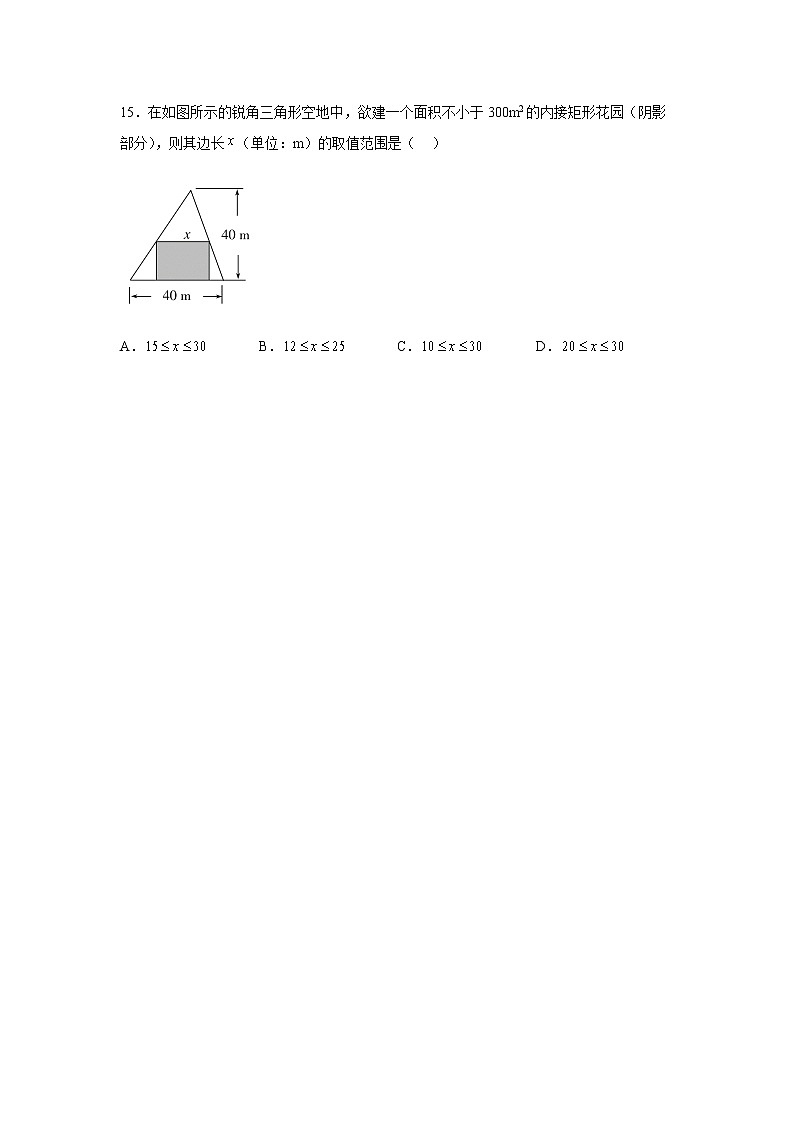
【精编】2.2.4均值不等式及其应用练习一、单选题1．若，，则的最小值是（    ）A． B． C．4 D．22．下列各式中，对任何实数都成立的一个式子是（    ）.A． B． C． D．3．已知a，b为非负数，且满足，则的最大值为（    ）A．40 B． C．42 D．4．已知正实数满足，则的最小值为（    ）A．6 B．8 C．10 D．125．设a>0，b>0.若是3a与32b的等比中项，则的最小值为（    ）A．8 B．4 C．1 D．6．已知，，，则的最小值为（    ）A．2 B．3 C． D．7．已知，，，则的最小值是（    ）A． B． C． D．8．已知 且，若恒成立，则实数m的取值范围是（    ）A．  B．} C． D．9．已知，则“”是“”的（    ）A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件10．已知，函数的最大值是（    ）A．4 B．-4 C．-6 D．-811．某小型服装厂生产一种风衣，日销售量 （件）与单价 （元）之间的关系为，生产件所需成本为（元），其中元，若要求每天获利不少于1300元，则日销售量的取值范围是（    ）.A． B．C． D．12．已知，，，，且，则下列不等式中，成立的个数有①，②，③，④（    ）A．1 B．2 C．3 D．413．设，且，则的最小值为（    ）A．4 B． C． D．614．玉溪某车间分批生产某种产品，每批的生产准备费用为800元，若每批生产件，则平均仓储时间为天，且每件产品每天的仓储费用为1元，为使平均到每件产品的生产准备费用与仓储费用之和最小，每批应生产产品A．60件 B．80件 C．100件 D．120件15．在如图所示的锐角三角形空地中，欲建一个面积不小于300m2的内接矩形花园（阴影部分），则其边长（单位：m）的取值范围是（    ）A． B． C． D．
参考答案与试题解析1．A【分析】利用基本不等式可求出和的最小值，相加可得出结果.【详解】由基本不等式得，当且仅当，时等号成立，因此，的最小值为.故选A.【点睛】本题考查利用基本不等式求和式的最小值，利用基本不等式求最值时也要注意条件“一正、二定、三相等”的成立，考查计算能力，属于基础题.2．C【分析】取特殊值可得选项A,B,D不恒成立，由可得选项C对应的不等式恒成立，得解.【详解】解：对于A，当时，根式无意义，故A不恒成立；对于B，当时，，故B不恒成立；对于C，，所以成立，故C成立；对于D，当时，，故D恒不成立，即对任何实数都成立的一个式子是，故选C.【点睛】本题考查了均值不等式的前提，重点考查了运算能力，属基础题.3．D【分析】将表示成的函数，利用均值不等式求出的范围即可求解作答.【详解】，又，当且仅当时取“=”，则，所以当时，的最大值为.故选：D4．B【分析】令，用分别乘两边再用均值不等式求解即可.【详解】因为，且为正实数所以，当且仅当即时等号成立.所以.故选：B.5．A【分析】根据等比中项可得a+2b=1，利用基本不等式及a+2b=1可求最小值.【详解】由题意可知3=3a32b=3a+2b，即a+2b=1.因为a>0，b>0，所以(a+2b)=+4≥2+4=8，当且仅当，即a=2b=时取“=”，所以的最小值为8.故选：A【点睛】本题主要考查了基本不等式的应用及不等式等号成立的条件，属于中档题.6．D【详解】根据题意，，∴，当且仅当且时等号成立，∴的最小值为，故选：D．7．C【分析】观察已知等式和所求式子均为非齐次式，考虑等式变形为 利用“1”的代换，化分式为齐次式，利用换元法，转化为函数问题求最值或利用基本不等式求最值.【详解】解法一：（转换成函数求最值）由题意，，，，即有且，将代入化简得：，令，∴，则有，当，有，单调递减；当，有单调递增，∴.故选C.解法二：（利用基本不等式求最值）由题意，，，，即有且，将代入化简得：，令，原式，当且仅当，即，等号成立，取到最小值.故选C.8．D【分析】根据基本不等式可取的最小值，从而可求实数m的取值范围.【详解】∵，且，∴，当且仅当时取等号，∴，由恒成立可得，解得：，故选：D.9．A【分析】由，结合基本不等式可得，由此可得，由此说明“”是“”的充分条件，再通过举反例说明“”不是“”的必要条件，由此确定正确选项.【详解】∵  ，∴  （当且仅当时等号成立），（当且仅当时等号成立），∴  （当且仅当时等号成立），若，则，∴  ，所以“”是“”的充分条件，当时，，此时，∴“”不是“”的必要条件，∴“”是“”的充分不必要条件，故选：A.10．B【解析】，，转化为求最小值，根据基本不等式求最小值【详解】由已知，则，，当且仅当， 时取等.所以；故选:B【点睛】本题考查用基本不等式求最值，掌握基本不等式求最值的条件：一正二定三相等是解题关键．11．B【分析】设该厂每天获得的利润为元，根据题意，求得利润为的函数关系式，得到一元二次不等式，即可求得，得到答案.【详解】设该厂每天获得的利润为元，则，，，根据题意，可得，解得，故当，且时，每天获得的利润不利于1300元.故选B.【点睛】本题主要考查了一元二次不等式的实际应用问题，其中解答中认真审题，列出关于的一元二次不等式，结合一元二次不等式的解答求解是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题.12．C【分析】分别利用二元、三元均值不等式可判断①和②的正确性；举特例可判断③是否正确；利用“1”的妙用可判断④的正确性.【详解】因，，，，且，于是有：，当且仅当时取“=”，①正确；，当且仅当时取“=”，②正确；时成立，而，③不正确；，当且仅当时取“=”，而，④正确，综上得：①②④共三个正确.故选：C【点睛】易错点睛：在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．13．C【分析】利用基本不等式“1”的代换求目标式的最小值，注意等号成立条件.【详解】由，当且仅当时等号成立.故选：C14．B【解析】确定生产件产品的生产准备费用与仓储费用之和，可得平均每件的生产准备费用与仓储费用之和，利用基本不等式，即可求得最值．【详解】解：根据题意，该生产件产品的生产准备费用与仓储费用之和是这样平均每件的生产准备费用与仓储费用之和为 （为正整数）由基本不等式，得当且仅当，即时，取得最小值，时，每件产品的生产准备费用与仓储费用之和最小故选：【点睛】本题考查函数的构建，考查基本不等式的运用，属于中档题，运用基本不等式时应该注意取等号的条件，才能准确给出答案，属于基础题．15．C【分析】根据三角形相似列出方程，将矩形的另一边用表示，再根据矩形的面积不小于300m2列出不等式，即可求出结果.【详解】设矩形的另一边长为m，则由三角形相似知，，所以，因为，所以，即，解得.故选:C【点睛】本题主要考查了一元二次不等式的应用，关键是建立数学模型，解一元二次不等式，属于基础题.