人教B版高中数学选择性必修第二册第三章排列、组合与二项式定理章末总结课件

这是一份人教B版高中数学选择性必修第二册第三章排列、组合与二项式定理章末总结课件，共36页。

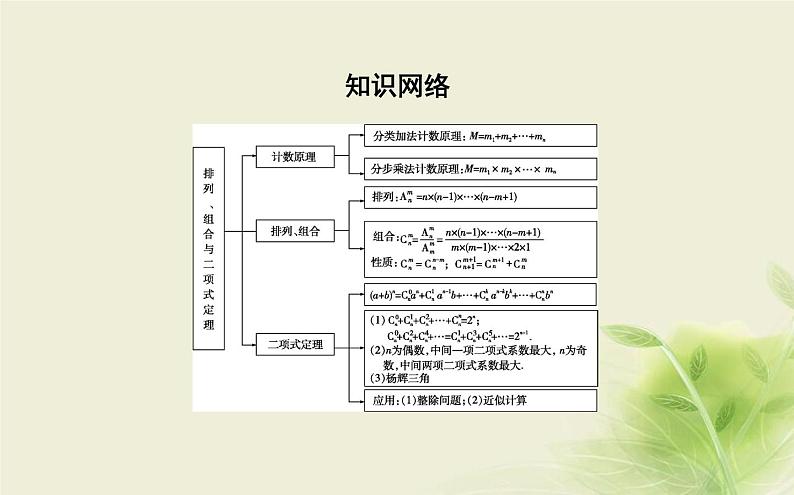
章末总结知识网络真题体验题型一　排列、组合[例1] (1)(2021·全国乙卷)将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有(　　)A.60种 B.120种 C.240种 D.480种答案:(1)C(2)(2018·全国Ⅰ卷)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有　　　　种.(用数字填写答案) 答案:(2)16[题组演练]1.(2020·海南卷)要安排3名学生到2个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有(　 　)A.2种 B.3种 C.6种 D.8种CC3.(2016·全国Ⅱ卷)如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为(　 　)A.24 B.18 C.12 D.9B4.(2018·浙江卷)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成　　　　个没有重复数字的四位数.(用数字作答) 答案:1 2605.(2017·天津卷)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有　　　　个.(用数字作答) 答案:1 080方法总结(1)合理的分类和分步,使用两个计数原理;(2)直接法和间接法;(3)特殊元素、特殊位置优先考虑;(4)掌握典型问题的解法,如“相邻问题捆绑法”“不相邻问题插空法”“分配问题先分组再分配”等.题型二　二项式定理答案:(1)C答案:(2)5　10(2)(2021·浙江卷)已知多项式(x-1)3+(x+1)4=x4+a1x3+a2x2+a3x+a4,则a1=　　　　,a2+a3+a4=　　　　.　 [题组演练]CC3.(2017·全国Ⅲ卷)(x+y)(2x-y)5的展开式中x3y3的系数为(　 　)A.-80 B.-40 C.40 D.80C答案:28答案:16　45.(2017·浙江卷)已知多项式(x+1)3(x+2)2=x5+a1x4+a2x3+a3x2+a4x+a5,则a4=　　 　　,a5=　　　　. 方法总结题型一　排列、组合1.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有(　 　)A.192种 B.216种 C.240种 D.288种模拟演练B2.(2021·河北承德高二月考)某校开设A类选修课3门,B类选修课3门,每位同学从中选3门.若要求两类课程中都至少选一门,则不同的选法共有(　　)A.3种 B.6种 C.9种 D.18种D3.(2021·安徽蚌埠高二月考)由数字1,2,3,4,5组成所有没有重复数字的五位数中,数字2和4不相邻的奇数共有(　 　)A.60个 B.48个 C.42个 D.36个D4.某医院组建的由7位专家组成的医疗队,按照 3人、2人、2人分成了三个小组,负责三个不同病房的医疗工作,则不同的安排方案共有(　 　)A.105种 B.210种C.630种 D.1 260种C5.某校周五的课程表设计中,要求安排8节课(上午4节、下午4节),分别安排语文、数学、英语、物理、化学、生物、政治、历史各一节,其中生物只能安排在第一节或最后一节,数学和英语在安排时必须相邻(注:上午的最后一节与下午的第一节不记作相邻),则周五的课程顺序的编排方法共有(　 　)A.4 800种 B.2 400种C.1 200种 D.240种A6.某医院开展“送医下乡”医疗义诊活动,现有五名医生被分配到四所不同的乡镇医院中,医生甲被指定分配到医院A,医生乙只能分配到医院A或医院B,医生丙不能分配到医生甲、乙所在的医院,其他两名医生分配到哪所医院都可以,若每所医院至少分配一名医生,则不同的分配方案共有(　 　)A.18种 B.20种 C.22种 D.24种B7.安排5名学生去3个社区进行志愿服务,且每人只去一个社区,要求每个社区至少有一名学生进行志愿服务,则不同的安排方式共有(　 　)A.360种 B.300种 C.150种 D.125种C8.中国古代中的“礼、乐、射、御、书、数”合称“六艺”.某校国学社团开展“六艺”课程讲座活动,每一艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在前三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同排课顺序共有(　 　)A.120种 B.156种 C.188种 D.240种A9.(2021·浙江桐乡高二月考)某校开设5门不同的数学选修课,每位同学可以从中任选1门或者2门课学习,甲、乙、丙三名同学选择的课没有一门是相同的,则不同的选法共有　　　　种. 答案:330题型二　二项式定理BB3.已知(x-1)5=a0+a1(x+1)+a2(x+1)2+…+a5(x+1)5,则a2等于(　 　)A.20 B.-20 C.80 D.-80D4.(1-x)(1+2x)4展开式中x2的系数为(　 　)A.-24 B.-8 C.16 D.24CA6.(多选题)(2021·辽宁大连高二期中)已知(2+x)(1-2x)4=a0+a1x+a2x2+a3x3+a4x4+a5x5,则(　 　)A.a0=2B.a3=-40C.a1+a2+a3+a4+a5=-1D.a1+a3+a5=39AB答案:4　24或968.已知(1-x)6=a0+a1x+a2x2+…+a6x6,则x2项的二项式系数是　　 　　,|a0|+|a1|+|a2|+…+|a6|=　　　 　. 答案:15　64