

高中数学人教B版 (2019)必修 第一册第三章 函数3.3 函数的应用(一)课后作业题
展开【名师】3.3函数的应用(一)作业练习
一、单选题
1.已知函数若函数有2个零点,则实数的取值范围是( )
A. B. C. D.
2.已知函数,则下列说法正确的个数为( )
①函数的定义域为;
②;
③函数的图象关于直线对称;
④当时,;
⑤函数的图象与x轴有4个交点.
A.2 B.3 C.4 D.5
3.已知函数是定义在R上的奇函数,当时,,则使不等式成立的x的取值范围是( )
A. B. C. D.
4.已知函数,若,,,则实数、、的大小关系为( )
A. B. C. D.
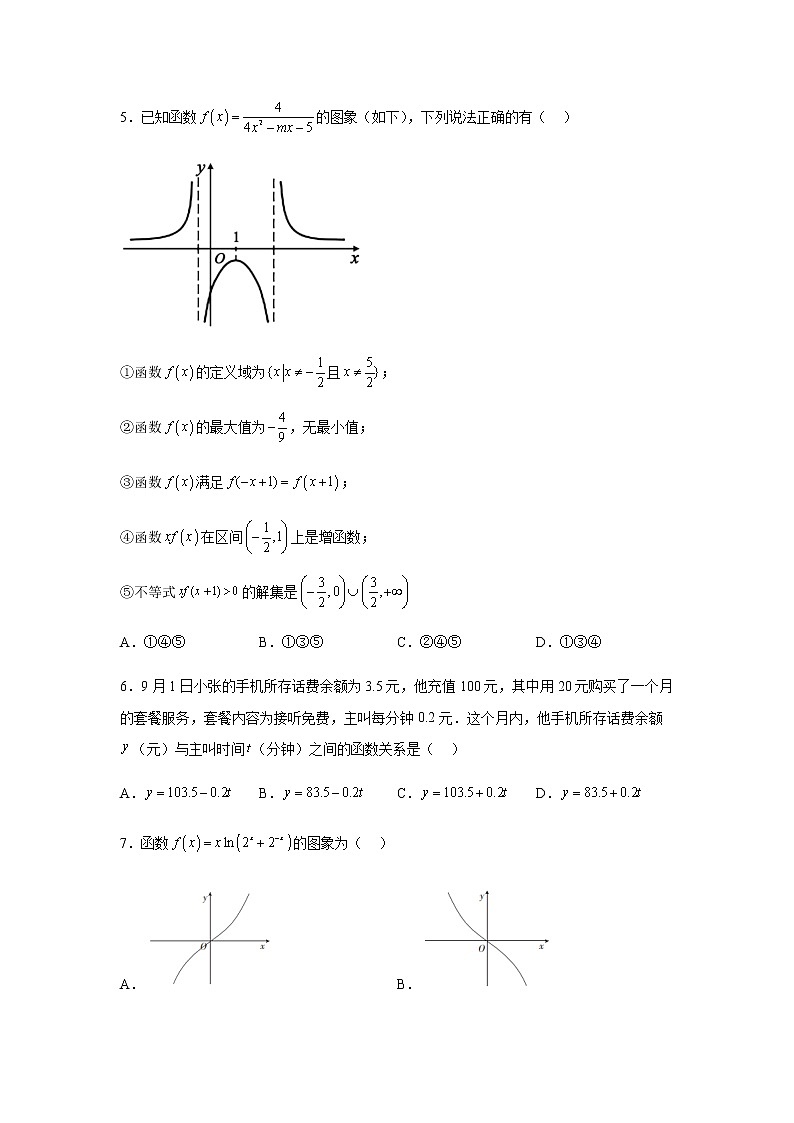
5.已知函数的图象(如下),下列说法正确的有( )
①函数的定义域为且;
②函数的最大值为,无最小值;
③函数满足;
④函数在区间上是增函数;
⑤不等式的解集是
A.①④⑤ B.①③⑤ C.②④⑤ D.①③④
6.9月1日小张的手机所存话费余额为3.5元,他充值100元,其中用20元购买了一个月的套餐服务,套餐内容为接听免费,主叫每分钟0.2元.这个月内,他手机所存话费余额(元)与主叫时间(分钟)之间的函数关系是( )
A. B. C. D.
7.函数的图象为( )
A. B.
C. D.
8.某人2015年7月1日到银行存入a元,若按年利率x复利计算,则到2018年7月1日可取款( )
A.元 B. C. D.
9.若函数有一个零点是,那么函数的零点是( )
A., B.,
C., D.,
10.将进货价为每个80元的商品按90元一个出售时,能卖出400个,每涨价1元,销售量就减少20个,为了使商家利润有所增加,则售价(元/个)的取值范围应是( )
A. B. C. D.
11.某市家庭煤气的使用量和煤气费(元)满足关系已知某家庭今年前四个月的煤气费如下表:
月份 | 一月份 | 二月份 | 三月份 | 四月份 |
用气量 | 4 | 5 | 25 | 35 |
煤气费/元 | 4 | 4 | 14 | 19 |
若五月份该家庭使用了的煤气,则其煤气费为( )A.12.5元 B.12元 C.11.5元 D.11元
12.如图,某池塘里浮萍的面积y(单位:)与时间(单位:月)的关系为,关于下列说法:
①浮萍每月的增长率为1;
②第5个月时,浮萍面积就会超过;
③浮萍每月增加的面积都相等;
④若浮萍蔓延到所经过的时间分别是,则,其中正确的说法是( )
A.①② B.①②③ C.①②④ D.①②③④
13.牛顿冷却定律描述一个事物在常温环境下的温度变化:如果物体的初始温度为,则经过一定时间后的温度满足,其中是环境温度,称为半衰期,现有一杯80℃的热水用来泡茶,研究表明,此茶的最佳饮用口感会出现在55℃.经测量室温为25℃,茶水降至75℃大约用时1分钟,那么为了获得最佳饮用口感,从泡茶开始大约需要等待( )(参考数据:,,)
A.4分钟 B.5分钟 C.6分钟 D.7分钟
14.某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过的,按每立方米元收费;用水超过的,超过部分加倍收费.某职工某月缴水费元,则该职工这个月实际用水为( )
A. B. C. D.
15.以下命题正确的是( )
A.函数的图像与垂直于轴的直线有且仅有一个交点
B.是函数是奇函数的充要条件
C.若函数在区间上有零点,则
D.函数是既奇又偶函数
参考答案与试题解析
1.A
【分析】根据的性质画出函数图像,将问题化为与有2个交点,数形结合求的范围.
【详解】由题意,与有2个交点,
当时,递增且值域为;
当时,在上递减,上递增且值域为;
所以的图像如下:
由图知:时,有2个零点.
故选:A
2.B
【分析】根据分母不等于0,求解函数的定义域,判断①;代入验证判断②;画出函数的图象,判断④⑤;画出函数和的图象,即可判断函数图象的交点个数.
【详解】函数的定义域为,故①错误;
,故②正确;
作出的图象如图所示,由图可知③错误,④正确.
令,得方程,
在上图中作出抛物线,由图可知的图象与抛物线有4个交点,
故函数的图象与轴有4个交点,故⑤正确.
故选:B.
3.C
【分析】由奇函数性质确定函数在R上的单调性,然后利用函数单调性化简不等式,再解指数不等式.
【详解】当时,是增函数且,又函数是定义在R上的奇函数,
则满足,所以,函数在上是连续函数,
所以函数在R上是增函数,
,∴
,∴,即,,又,∴,,即原不等式的解集为.
故选:C.
【点睛】本题考查函数的奇偶性与单调性,考查解指数不等式.利用奇偶性与单调性可化函数不等式为一般的无函数号“f”的不等式,在解指数不等式时要注意指数函数的值域,即.
4.D
【解析】利用定义可得出函数为偶函数,利用单调性定义可判断出函数在区间上为增函数,可得出,再利用中间值法比较、、三个数的大小关系,由函数在区间上的单调性可得出、、的大小关系.
【详解】函数的定义域为,,该函数为偶函数,
当时,
,
则函数在区间上为增函数,
则,
指数函数为增函数,则,
对数函数在上为增函数,则,即,
,则,因此,.
故选:D.
【点睛】本题考查利用函数的单调性与奇偶性比较函数值的大小关系,同时也考查了指数式与对数式的大小比较,考查推理能力,属于中等题.
5.B
【分析】由函数图象得对称轴,求得值,然后可得定义域,由图象可得最值情况,可判断出①②③,令,然后则单调性定义确定单调性后判断④,结合函数图象分类讨论解不等式后判断⑤.
【详解】由图象并结合函数的性质可知对称轴为,故,解得.
因为,解得且,其定义域为且,故①正确.
由图象可知函数无最大值,也无最小值,故②错误.
又由函数图象关于对称,即是偶函数,所以,故③正确﹒
令,任取,且,
则
化简得,
由图可知且.
由可知,又因为,所以
所以函数在区间上是减函数,故④错误.
由可知,当时,,
即或,解得或(舍后者),故;
当时,,即,解得,取.
综合两种情况得的取值范围是:或,故⑤正确.所以①③⑤正确,
故选:B.
6.B
【分析】由题意,话费余额与主叫时间之间的函数关系满足一次函数,由题设条件分析可得解的值
【详解】由题意,手机所存话费余额(元)与主叫时间(分钟)之间的函数关系满足一次函数
不妨设为,可知当时,,故
且主叫每分钟0.2元,故
故函数关系为:
故选:B
7.A
【分析】先求判断函数的奇偶性,再取即可选出符合题意图象.
【详解】由,故函数为奇函数,图象关于原点对称,又,
故选:A.
8.D
【分析】按复利的计算办法直接计算即可
【详解】由题意知,2016年7月1日可取款元,
2017年7月1日可取款
2018年7月1日可取款元.
故选:D
9.C
【分析】根据题意,得到,推出,解对应的方程,即可得出结果.
【详解】因为函数有一个零点是,所以,,
所以,
由得或,
故的零点是,.
故选:C.
【点睛】本题主要考查求函数零点,属于基础题型.
10.A
【分析】首先设每个涨价元,涨价后的利润与原利润之差为元,结合条件列式,根据,求的取值范围,即可得到的取值范围.
【详解】设每个涨价元,涨价后的利润与原利润之差为元,
则.
要使商家利润有所增加,则必须使,即,得,所以的取值为.
故选:A
11.A
【分析】根据表格数据列方程组解出未知数,即可求得.
【详解】根据表格可得:,
根据三月和四月的数据可得:,解得:
所以,.
故选:A
12.C
【分析】利用指数函数的性质与对数运算,结合图像逐一判断即可.
【详解】因为图像过,所以由,所以,故原题中函数关系为
对于①:,所以每个月的增长率为1,故①正确;
对于②:当时,,故②正确;
对于③:第二个月比第一个月增加
第三个月比第二个月增加,故③错误;
对于④:由题,所以,所以,故④正确;
故选:C
13.C
【分析】根据已知条件代入公式计算得到,再把该值代入,利用对数的运算即可求得结果.
【详解】根据题意,,即
设茶水从降至大约用时t分钟,则,
即,即
两边同时取对数:
解得,所以从泡茶开始大约需要等待分钟
故选:C
【点睛】关键点点睛:本题考查了函数的实际应用,考查了对数的运算性质,解题的关键是熟练运用对数的运算公式,考查学生的审题分析能力与运算求解能力,属于基础题.
14.A
【分析】先写出用水量与电费发函数关系,再解方程.
【详解】设该职工用水时,缴纳的水费为元,由题意得,
则,解得.
答:该职工这个月实际用水为.
故选:A
【点睛】解应用题关键是找出变量之间的关系,列方程求解未知量.
15.D
【解析】A.根据函数的对应关系判断选项;B.根据奇函数与的关系判断选项;C.根据零点存在性定理判断选项;D.先求函数的定义域,再根据函数的奇偶性的定义判断选项.
【详解】A. 函数的图像与垂直于轴的直线的交点个数是0个或1个,故A不正确;
B.不能推出函数是奇函数,例如,若函数是奇函数,定义域里没有,函数也不过原点,所以是函数是奇函数的既不充分也不必要条件,故B不正确;
C. 若函数在区间上有零点,,在区间有零点,但,故C不正确;
D.函数的定义域是,解得:,即,,函数既满足,又满足,所以函数既是奇函数,又是偶函数.
故选:D
高中数学3.3 函数的应用(一)同步达标检测题: 这是一份高中数学3.3 函数的应用(一)同步达标检测题,共14页。试卷主要包含了单选题等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第一册3.3 函数的应用(一)同步练习题: 这是一份高中数学人教B版 (2019)必修 第一册3.3 函数的应用(一)同步练习题,共11页。试卷主要包含了单选题等内容,欢迎下载使用。
高中数学人教B版 (2019)必修 第一册3.3 函数的应用(一)课后复习题: 这是一份高中数学人教B版 (2019)必修 第一册3.3 函数的应用(一)课后复习题,共14页。试卷主要包含了单选题等内容,欢迎下载使用。













