高中数学人教B版 (2019)必修 第一册3.3 函数的应用(一)课后复习题

【特供】3.3函数的应用（一）课时练习

一、单选题

1．若函数的定义域为 ，值域为，则的取值范围是

A． B． C． D．

2．一种新型电子产品计划投产两年后，使成本降36%，那么平均每年应降低成本（    ）

A．18% B．20%

C．24% D．36%

3．已知函数，其中表示不超过实数的最大整数，关于有下述四个结论：

①的一个周期是；    ②是非奇非偶函数；

③在单调递减；    ④的最大值大于．

其中所有正确结论的编号是（    ）

A．①②④ B．②④ C．①③ D．①②

4．已知当时，，则以下判断正确的是（   ）

A． B．

C． D．

5．已知函数，，若有且只有两个不等的实数根，则a的取值范围为（    ）

A． B． C． D．

6．定义在R上的奇函数满足，且在[0,1上单调递减，若方程在[0,1上有实数根，则方程在区间[-1,7]上所有实根之和是（    ）

A．12 B．14 C．6 D．7

7．已知函数的定义域为 ，且函数的图象关于点对称，对于任意的，总有成立，当时，，函数（），对任意，存在，使得成立，则满足条件的实数构成的集合为（   ）

A． B．

C． D．

8．若方程有两个不相等的实数根，则实数的取值范围是（   ）

A． B． C．，且 D．，且

9．为配制一种药液，进行了三次稀释，先在体积为的桶中盛满纯药液，第一次将桶中药液倒出10升后用水补满，搅拌均匀第二次倒出8升后用水补满，然后第三次倒出10升后用水补满.若第二次稀释后桶中药液含量不超过容积的60%，则第三次稀释后桶中的药液所占百分比的最大值为（    ）

A．55% B．50% C．45% D．40%

10．已知函数，若关于的不等式的解集为，则

A． B．

C． D．

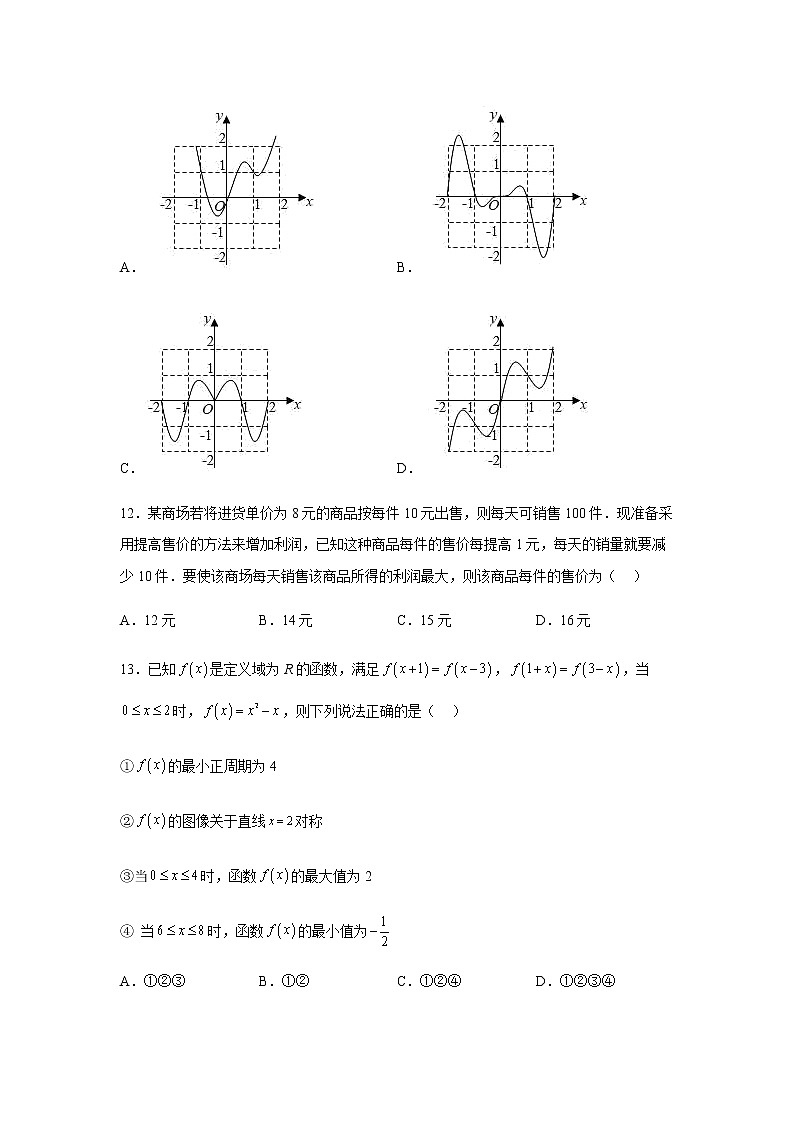
11．函数的图象是（    ）

A．  B．

C． D．

12．某商场若将进货单价为8元的商品按每件10元出售，则每天可销售100件．现准备采用提高售价的方法来增加利润，已知这种商品每件的售价每提高1元，每天的销量就要减少10件．要使该商场每天销售该商品所得的利润最大，则该商品每件的售价为（    ）

A．12元 B．14元 C．15元 D．16元

13．已知是定义域为R的函数，满足，，当时，，则下列说法正确的是（    ）

①的最小正周期为4                

②的图像关于直线对称

③当时，函数的最大值为2    

④ 当时，函数的最小值为

A．①②③ B．①② C．①②④ D．①②③④

14．某地一天内的气温（单位：）与时刻（单位：）之间的关系如图所示，令表示时间段内的温差（即时间段内最高温度与最低温度的差），则与之间的函数图像大致是

A． B．

C． D．

15．为实现碳达峰、碳中和奠定坚实基础，《中共中央国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》中提出，到年单位国内生产总值二氧化碳排放比年下降，则年至年要求单位国内生产总值二氧化碳排放的年均减排率最低是（    ）

A． B．

C． D．

参考答案与试题解析

1．D

【分析】由二次函数的图象和特殊点的函数值可得选项.

【详解】如图

令，则，

又函数的定义域为，值域为，所以，

故选：D.

【点睛】本题考查二次函数的图象与值域，关键在于观察二次函数的对称轴与所求的区间的关系，属于基础题.

2．B

【分析】设平均每年降低成本x，由题意可列方程(1－x)2＝0.64，解方程可得答案

【详解】设平均每年降低成本x，

解得或（舍去），

故选：B

3．A

【解析】根据函数周期的定义判断①正确，利用特值判断函数是非奇非偶函数，得到②正确，根据取整函数的定义，可以判断在上函数值是确定的一个值，得到③错误，利用得到④正确，从而得到结果.

【详解】因为，

所以的一个周期是，①正确；

又，④正确；

又，

，

所以，，所以是非奇非偶函数，所以②正确；

当时，，，所以，所以，所以③错误；

综上所以正确的结论的序号是①②④，

故选：A．

【点睛】该题考查三角函数相关性质的辨析，涉及到的知识点有取整函数，奇偶性、单调性、周期性的综合应用，属于较难题目.

4．C

【解析】先构造函数，得出函数的奇偶性和单调性求出，从而得出选项即可.

【详解】记，

为偶函数且在上单调递减，

由，

得到，

即，

∴，

即.

故选：C.

【点睛】本题主要考查了利用函数的奇偶性和单调性比较大小的问题.属于较易题.

5．B

【分析】根据选项特点使用排除法，分进行讨论，然后简单计算以及判断可得结果.

【详解】当时，，

则

所以无解，故，排除

当时，，令

则

则，不符合题意，故，排除D

故选：B

【点睛】本题考查方程根的个数求解参数，对于选填，可以使用排除法、特殊值法等小技巧，使复杂问题简单化，达到解决问题的目的，属中档题.

6．A

【分析】由已知可知是周期为4的奇函数且关于对称，再利用奇函数、周期函数的性质判断在[-1,7]上各子区间的单调性及的根所在区间，结合对称性求所有实根之和.

【详解】由题设，，又为奇函数，

∴，即，

∴是周期为4的奇函数且关于对称，

又在[0,1上单调递减，则[-1,0上递减，(1,2、(2,3上递增，

∴由周期性知：(3,4、[4,5上递减，(5,6、(6,7上递增，

∵在[0,1上有实数根，则在[-1,0上有实数根，

∴综上，结合对称性知：在[-1,0 、(2,3、(3,4、(6,7各 有一个实数根，且关于对称，

∴在区间[-1,7]上所有实根之和为12.

故选：A

7．A

【分析】由的特性结合函数图象平移变换可得是奇函数，由可得函数的周期，由此探讨出的值域，再将所求问题转化为不等式在上有解即可.

【详解】由函数的图象关于点对称知函数的图象关于原点对称，即函数是奇函数，

由任意的，总有成立，即恒成立，于是得函数的周期是4，

又当时，，则当时，，而是奇函数，当时，，

又，f(-2)=-f(2)，从而得，即时，，

而函数的周期是4，于是得函数在上的值域是，

因对任意，存在，使得成立，从而得不等式，即在上有解，

当时，取，成立，即得，

当时，在上有解，必有，解得，则有，

综上得，

所以满足条件的实数构成的集合为.

故选：A

8．C

【分析】由题意可得，从而可求出实数的取值范围.

【详解】解：由方程有两个不相等的实数根可知，此方程为一元二次方程且判别式大于零，即可得

，解得，且.

故选:C.

【点睛】本题考查了一元二次方程根的分布问题.本题的关键是由不同两根得判别式大于零.本题的易错点是忽略了这一条件.

9．C

【分析】根据题意表达出第二次稀释后桶中药液含量，列出不等式，求出体积的范围，再表达出第三次倒出10升后用水补满，桶中的农药占容积的比率不超过，根据体积的取值范围，求出最值.

【详解】第二次倒出后桶中剩余农药升，则，即，解得：，又，∴.

第三次倒出10升后用水补满，桶中的农药占容积的比率不超过，

∵，

∴，

故选：C.

10．B

【分析】由题意可得，且，3为方程的两根，运用韦达定理可得，，的关系，可得的解析式，计算，（1），（4），比较可得所求大小关系．

【详解】关于的不等式的解集为，

可得，且，3为方程的两根，

可得，，即，，

，，

可得，（1），（4），

可得（4）（1），故选．

【点睛】本题主要考查二次函数的图象和性质、函数与方程的思想，以及韦达定理的运用．

11．D

【解析】根据函数的奇偶性和特殊点的函数值的符号，结合选项，即可求解．

【详解】由题意，函数的定义域为，

且，

所以函数为奇函数，图象关于原点对称，排除A、C；

当时，，排除B．

故选：D．

【点睛】本题主要考查了函数图象的识别，其中解答中熟练应用函数的基本性质和特殊点的函数值求解是解答的关键，着重考查了推理与识别能力．

12．B

【分析】设该商品每件的售价为x元，根据给定条件列出关于x的函数关系，借助函数最值求解作答.

【详解】设该商品每件的售价为x元，则每件商品售出所获利润为元，销售量为件，

商场每天销售该商品所得的利润，

当时，(元)，

所以该商品每件的售价为14元.

故选：B

13．A

【分析】①利用求出函数的周期；②利用求出函数的对称轴；③④先求出当时，的单调性，再利用函数的周期和对称轴进行求解.

【详解】对于①，，，则，即的最小正周期为4，故①正确；

对于②，由知的图像关于直线对称，故②正确；

对于③，当时，在上单调递减，在上单调递增

根据对称性可知，函数在，上单调递减，在，上单调递增，则函数在上的最大值为，故③正确；

对于④，根据周期性以及单调性可知，函数在上单调递减，在上单调递增，则函数在上的最小值为，故④错误.

故选：A

14．D

【分析】根据题意，分析函数图像的特征，可得函数过原点，在上，不断增大，在上，先是一个定值，然后增大，在上，是个定值，分析选项可得答案．

【详解】由题图看出，时，，排除B；在上，不断增大，在上，先是一个定值，然后增大，在上，不断增大，在上，是个定值，在上，不断增大，

故选D.

【点睛】本题考查函数图像与图像的变化，属于基础题．

15．B

【分析】由题意可知至年剩下的二氧化碳排放比年不能多于，由此列出相应不等式，解得答案.

【详解】设年均减排率最低是x,由题意可知至年碳排放比下降，

那么至年碳排放比年剩下的不多于，

则 ，解得，

故选：B