高中数学人教B版 (2019)必修 第一册3.3 函数的应用(一)同步练习题

【基础】3.3函数的应用（一）同步练习

一、单选题

1．已知函数，，若有且只有两个不等的实数根，则a的取值范围为（    ）

A． B． C． D．

2．为实现碳达峰、碳中和奠定坚实基础，《中共中央国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》中提出，到年单位国内生产总值二氧化碳排放比年下降，则年至年要求单位国内生产总值二氧化碳排放的年均减排率最低是（    ）

A． B．

C． D．

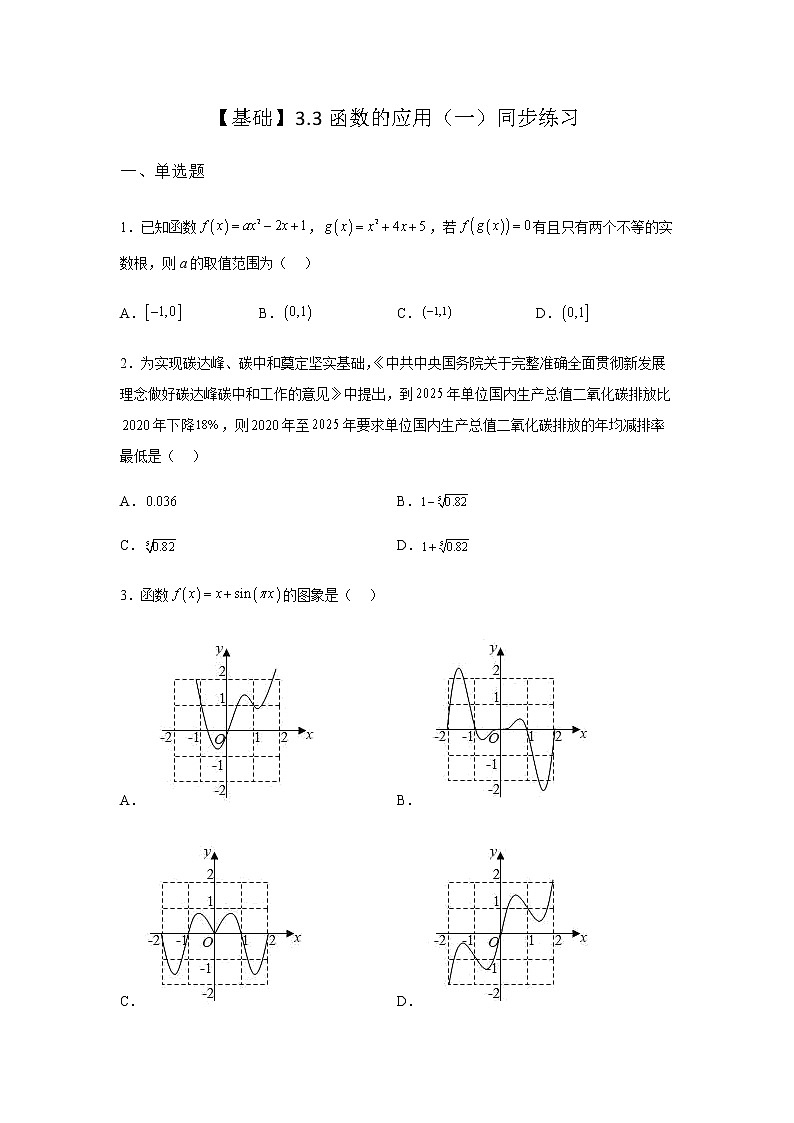
3．函数的图象是（    ）

A．  B．

C． D．

4．函数的零点所在的区间为（    ）

A． B． C． D．

5．已知函数，则下列说法正确的个数为（    ）

①函数的定义域为；

②；

③函数的图象关于直线对称；

④当时，；

⑤函数的图象与x轴有4个交点．

A．2 B．3 C．4 D．5

6．某公司今年销售一种产品，一月份获得利润万元，由于产品畅销，利润逐月增加，第一季度共获利万元，已知二月份和三月份利润的月增长率相同.设二、三月份利润的月增长率为，则满足的方程为（    ）

A．

B．

C．

D．

7．已知函数为一次函数，若，有，当时，函数的最大值与最小值之和是（    ）

A．10 B．8 C．7 D．6

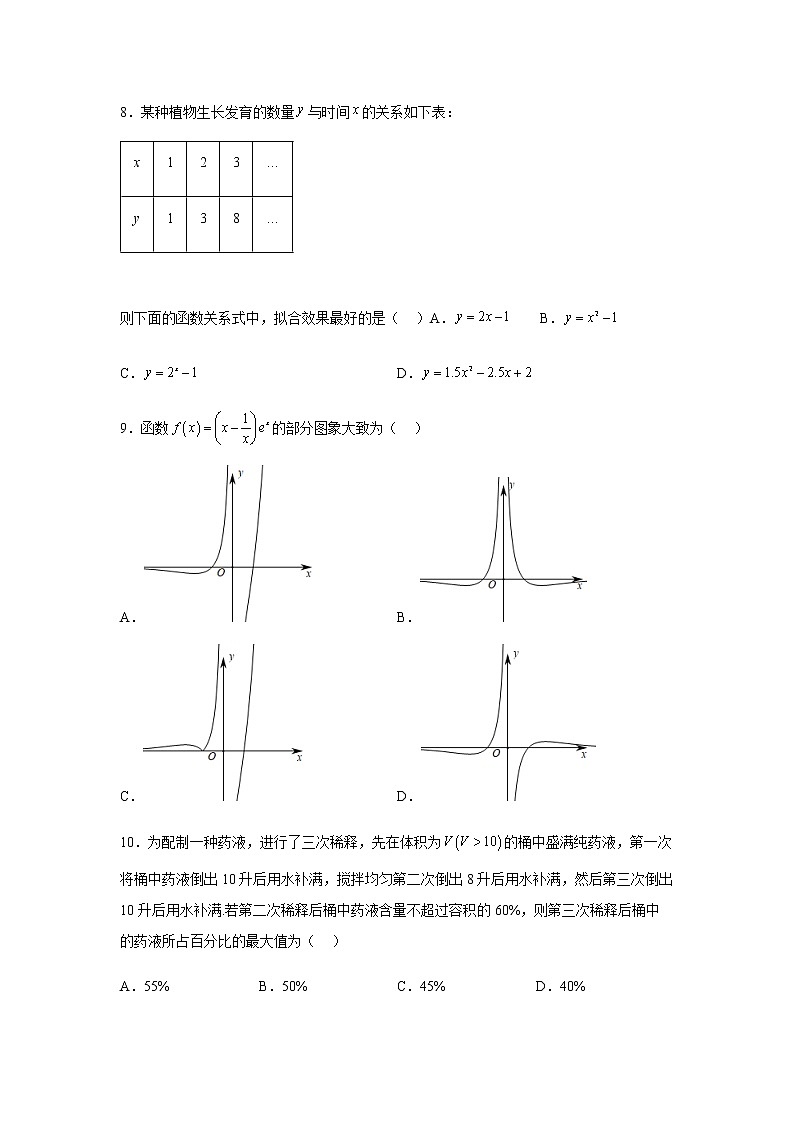
8．某种植物生长发育的数量与时间的关系如下表：

则下面的函数关系式中，拟合效果最好的是（    ）A．  B．

C． D．

9．函数的部分图象大致为（    ）

A． B．

C． D．

10．为配制一种药液，进行了三次稀释，先在体积为的桶中盛满纯药液，第一次将桶中药液倒出10升后用水补满，搅拌均匀第二次倒出8升后用水补满，然后第三次倒出10升后用水补满.若第二次稀释后桶中药液含量不超过容积的60%，则第三次稀释后桶中的药液所占百分比的最大值为（    ）

A．55% B．50% C．45% D．40%

11．通过研究学生的学习行为，心理学家发现，学生的接受能力依赖于老师引入概念和描述所用的时间．若用表示学生掌握和接受概念的能力（越大，表示学生的接受能力越强），表示提出和讲授概念的时间（单位：），长期的实验和分析表明，与有以下关系：则下列说法错误的是（    ）

A．讲授开始时，学生的兴趣递增；中间有段时间，学生的兴趣保持较理想的状态；随后学生的注意力开始分散

B．讲课开始后第5分钟比讲课开始第20分钟，学生的接受能力更强一点

C．讲课开始后第10分钟到第16分钟，学生的接受能力最强

D．需要13分钟讲解的复杂问题，老师可以在学生的注意力至少达到55以上的情况下完成

12．定义在R上的奇函数满足，且在[0,1上单调递减，若方程在[0,1上有实数根，则方程在区间[-1,7]上所有实根之和是（    ）

A．12 B．14 C．6 D．7

13．定义在上的函数满足.若的图象关于直线对称，则下列选项中一定成立的是（    ）

A． B． C． D．

14．若定义在R上的增函数的图象关于点对称，且，则下列结论不一定成立的是（    ）

A． B．

C． D．

参考答案与试题解析

1．B

【分析】由题意可知至年剩下的二氧化碳排放比年不能多于，由此列出相应不等式，解得答案.

【详解】设年均减排率最低是x,由题意可知至年碳排放比下降，

那么至年碳排放比年剩下的不多于，

则 ，解得，

故选：B

2．D

【解析】根据函数的奇偶性和特殊点的函数值的符号，结合选项，即可求解．

【详解】由题意，函数的定义域为，

且，

所以函数为奇函数，图象关于原点对称，排除A、C；

当时，，排除B．

故选：D．

【点睛】本题主要考查了函数图象的识别，其中解答中熟练应用函数的基本性质和特殊点的函数值求解是解答的关键，着重考查了推理与识别能力．

3．C

【解析】先判断出函数的单调性,结合零点存在定理即可判断出零点所在区间.

【详解】函数

所以函数在R上单调递增

因为

所以函数零点在

故选:C

【点睛】本题考查了根据零点存在定理判断零点所在区间,注意需判断函数的单调性,说明零点的唯一性,属于基础题.

4．B

【分析】根据分母不等于0，求解函数的定义域，判断①；代入验证判断②；画出函数的图象，判断④⑤；画出函数和的图象，即可判断函数图象的交点个数.

【详解】函数的定义域为，故①错误；

，故②正确；

作出的图象如图所示，由图可知③错误，④正确．

令，得方程，

在上图中作出抛物线，由图可知的图象与抛物线有4个交点，

故函数的图象与轴有4个交点，故⑤正确．

故选：B．

5．D

【分析】分别求出二、三份的利润再求和即可.

【详解】二、三月份利润的月增长率为，

则二月份获得利润为万元，三月份获得利润为万元，

依题意得：.

故选：D.

6．D

【解析】设，求得，得到，再设，得到函数为单调递增函数，且为是奇函数，即可求解.

【详解】由题意，设一次函数，

因为，可得，解得，

所以，故的图象关于对称，

又设，可得函数为单调递增函数，

且，

即，所以是奇函数，则，

则，，

所以

即为的最大值与最小值之和6.

故选：D.

【点睛】本题主要考查了一次函数的图象与性质，对数运算性质，以及函数的单调性与奇偶性的综合应用，着重考查了推理与运算能力.

7．D

【分析】将各数据代入选项，依次判断即可得到结论.

【详解】由题知：

当时，，而选项B，当时，，故排除B.

当时，，而选项A，当时，，故排除A，

选项C，当时，，故排除C，

选项D，当时，，时，，D正确.

故选：D

【点睛】本题主要考查函数模型的选择，考查学生分析问题的能力，属于简单题.

8．A

【分析】根据函数奇偶性排除BD，利用特殊点的函数值大小排除C.

【详解】当时，，故，又因为，所以，排除C．因为，不恒等于0，且不恒等于，所以既不是奇函数也不是偶函数，排除B，D．

故选：A

9．C

【分析】根据题意表达出第二次稀释后桶中药液含量，列出不等式，求出体积的范围，再表达出第三次倒出10升后用水补满，桶中的农药占容积的比率不超过，根据体积的取值范围，求出最值.

【详解】第二次倒出后桶中剩余农药升，则，即，解得：，又，∴.

第三次倒出10升后用水补满，桶中的农药占容积的比率不超过，

∵，

∴，

故选：C.

10．A

【分析】由已知可知是周期为4的奇函数且关于对称，再利用奇函数、周期函数的性质判断在[-1,7]上各子区间的单调性及的根所在区间，结合对称性求所有实根之和.

【详解】由题设，，又为奇函数，

∴，即，

∴是周期为4的奇函数且关于对称，

又在[0,1上单调递减，则[-1,0上递减，(1,2、(2,3上递增，

∴由周期性知：(3,4、[4,5上递减，(5,6、(6,7上递增，

∵在[0,1上有实数根，则在[-1,0上有实数根，

∴综上，结合对称性知：在[-1,0 、(2,3、(3,4、(6,7各 有一个实数根，且关于对称，

∴在区间[-1,7]上所有实根之和为12.

故选：A

11．A

【分析】根据题意，利用对称性，得到，再利用，对进行赋值，然后可求解.

【详解】函数的图象关于直线对称，则必有，所以，,

,又因为满足，取，所以，，，则，取，则，A对；

故选：A

12．A

【分析】根据题意，求得得单调性和奇偶性，再针对每个选项进行逐一分析即可.

【详解】因为的图像关于对称，

所以的图像关于对称，且是定义在R上的增函数，

所以是在R上的奇函数，且在R上为增函数，

所以，

所以对于A：，因为不一定等于1，所以不一定成立；

对于B：，成立；

对于C：，成立；

对于D：，

因为在R上为增函数，故，

所以成立.

故选：A.

【点睛】本题考查函数对称性以及单调性的综合应用，属基础题.

13．B

【分析】根据解析式依次求出函数的定义域、奇偶性、函数值，用排除法得出结论．

【详解】解：∵，∴函数的定义域为，

又，

则函数是奇函数，图象关于原点对称，故排除A选项；

又，故排除C、D两个选项；

故选：B．

【点睛】本题主要考查函数图象的识别，一般根据函数的定义域、奇偶性、特殊点的函数值、单调性解题，一般用排除法，属于中档题．