2021届云南师范大学附属中学高三高考适应性月考卷（一）数学（理）试题 PDF版

云南师大附中2021届高考适应性月考卷（一）

理科数学参考答案

一、选择题（本大题共12小题，每小题5分，共60分）

【解析】

1．M是数集，N是点集，故选C．

2．，故选D．

3．随机变量x~，正态曲线的对称轴，所以，故选A．

4．，故选C．

5．，故选A．

6．双曲线右焦点，即，点F到一条渐近线的距离为b，即，∴，，故选B．

7．由题意，．所以 ，，故选A．

8．由，解得(舍负)，又由，得，所以 ，当且仅当，时，等号成立，但是m，，故，时，最小值为，故选D．

9．由题意三视图对应的几何体如图1所示，所以几何体的体积为正方体的体积减去2个三棱锥的体积，即，故选D．

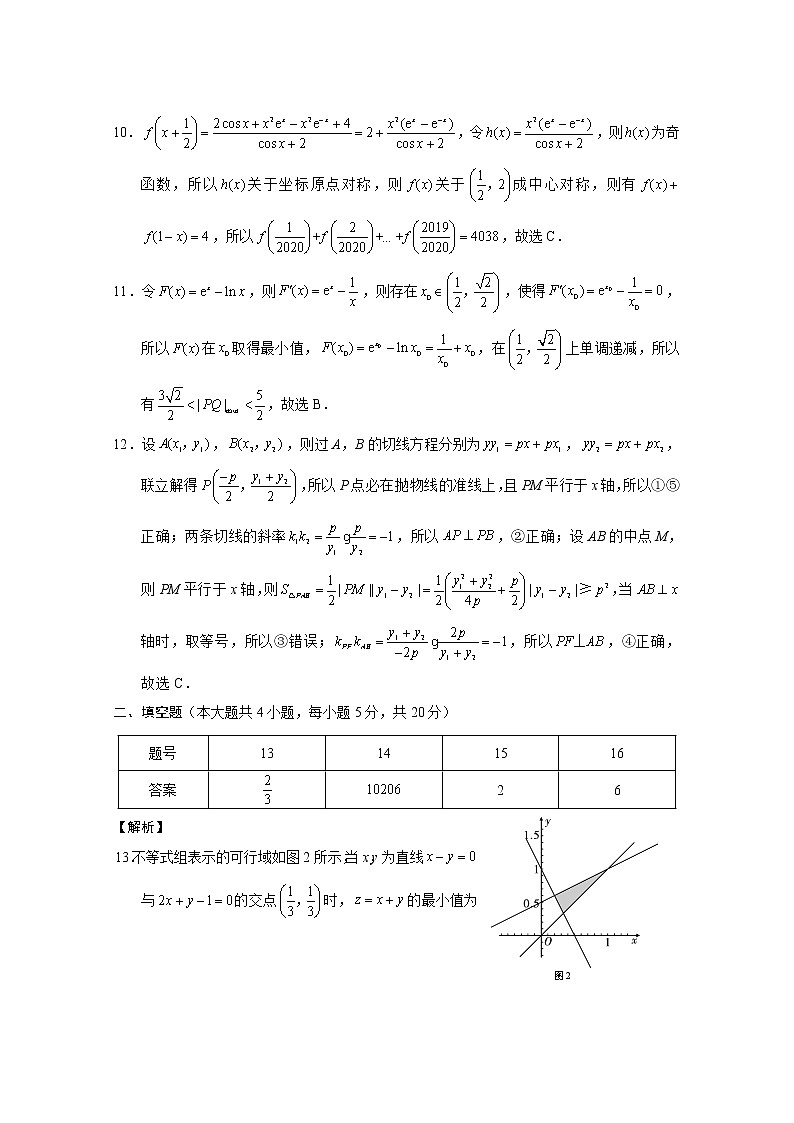
10．，令，则为奇函数，所以关于坐标原点对称，则关于成中心对称，则有 ，所以，故选C．

11．令，则，则存在，使得，所以在取得最小值，，在上单调递减，所以有，故选B．

12．设，，则过A，B的切线方程分别为，，联立解得，所以P点必在抛物线的准线上，且PM平行于x轴，所以①⑤正确；两条切线的斜率，所以，②正确；设AB的中点M，则PM平行于x轴，则，当轴时，取等号，所以③错误；，所以，④正确，故选C．

二、填空题（本大题共4小题，每小题5分，共20分）

【解析】

13．不等式组表示的可行域如图2所示，当x，y为直线与的交点时，的最小值为.

14．的展开式的通项公式，令，解得，所以的系数为10206．

15．圆C：的圆心为，四边形PACB的面积，所以当PC最小时，四边形PACB面积最小．代入点到直线的距离公式，，故四边形PACB面积的最小值为2．

16．如图3，由对称性知，球O的球心在中垂线MN上，设球O的半径为R，在中，由勾股定理可得在中，由勾股定理可得，

，由，联立解得．

三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤）

17．（本小题满分12分）

解：（1）已知，

由正弦定理，，

整理得，

由余弦定理：，又，

所以． ………………………………………………………………（4分）

（2）已知，

整理得，

，

即．

①当时，为直角三角形，；

②当时，，

所以，为等边三角形，． ……………………（12分）

18．（本小题满分12分）

解：（1）x的值为，

数学成绩在90分以上的人数：．

 …………………………………………………………（4分）

（2）把频率作为概率，从该市所有的中学生中任取一人，

成绩在110以上的概率，

所以从该市所有的中学生（人数很多）中随机选取4人，

所选4人中成绩在110以上的人数，

随机变量的取值可能为0，1，2，3，4，

，

，

，

，

，

随机变量的分布列

随机变量数学期望． ……………………………（12分）

19．（本小题满分12分）

（1）证明：如图4，

    ∵平面ABC，平面ABC，

∴．

又∵，∵，

∴．

又∵，

∴平面平面． ………………………………………………（4分）

（2）解：过点A作平面ABC的垂线作为z轴，AB为x轴，AC为y轴，建立如图5所示的空间直角坐标系，

则，，，，

，

设平面的法向量，

则有令，，

设平面的法向量，

则有令，，

向量，所成角的余弦值：．

∴，

∴二面角的正弦值为． ……………………………………（12分）

20．（本小题满分12分）

（1）解：由，得，

又在椭圆上，

代入椭圆方程有，解得，

所以椭圆C的标准方程为． ………………………………………（4分）

（2）证明：当直线l的斜率不存在时，，，

，解得，不符合题意；

当直线l的斜率存在时，设直线l的方程，，，

由整理得，

，，．

由，整理得，

即．

当时，此时，直线l过P点，不符合题意；

当时， 有解，此时直线l：过定点．

 ……………………………………………………（12分）

21．（本小题满分12分）

（1）解：函数的定义域为，

，解得(舍去)，．

当时，在上恒成立，所以函数单调递增；

当时，在上，函数单调递减，

在上，函数单调递增． ……………………………（4分）

（2）证明：由（1）知，当时，在上，函数单调递减；

在上，函数单调递增，

当时，，当时，，

而当时，，

所以函数的图象与x轴有两个交点．

设，，则有，

要证，只需证，

设，令，

则有，

，

在上单调递减，又，

所以，即，

又，则有，

而由已知，所以．

又，，函数在上单调递增，

所以，即，命题得证． ……………………………（12分）

22．（本小题满分10分）【选修4−4：坐标系与参数方程】

解：（1）由曲线的参数方程(为参数)，

消参得曲线的直角坐标方程为，

由得曲线的极坐标方程为．

曲线的极坐标方程为， ………………………………（5分）

（2），

点到直线的距离，

所以． ………………………………………（10分）

23．（本小题满分10分）【选修4−5：不等式选讲】

解：（1）由绝对值不等式，

所以． ………………………………………………………………（5分）

（2）由（1）知：，即，所以，

由柯西不等式：

，

当且仅当，等号成立． …………………………………………（10分）