人教B版高中数学选择性必修第三册6-2-2导数与函数的极值、最值随堂作业含答案2

【名师】6.2.2 导数与函数的极值、最值随堂练习

一．单项选择

1．

若函数的最小值为，则（    ）

A． B． C． D．

2．

已知，，，则（    ）

A． B．

C． D．

3．

已知定义在R上的可导函数的导函数为，若当时，，则函数的零点个数为（    ）

A．0 B．1 C．2 D．0或2

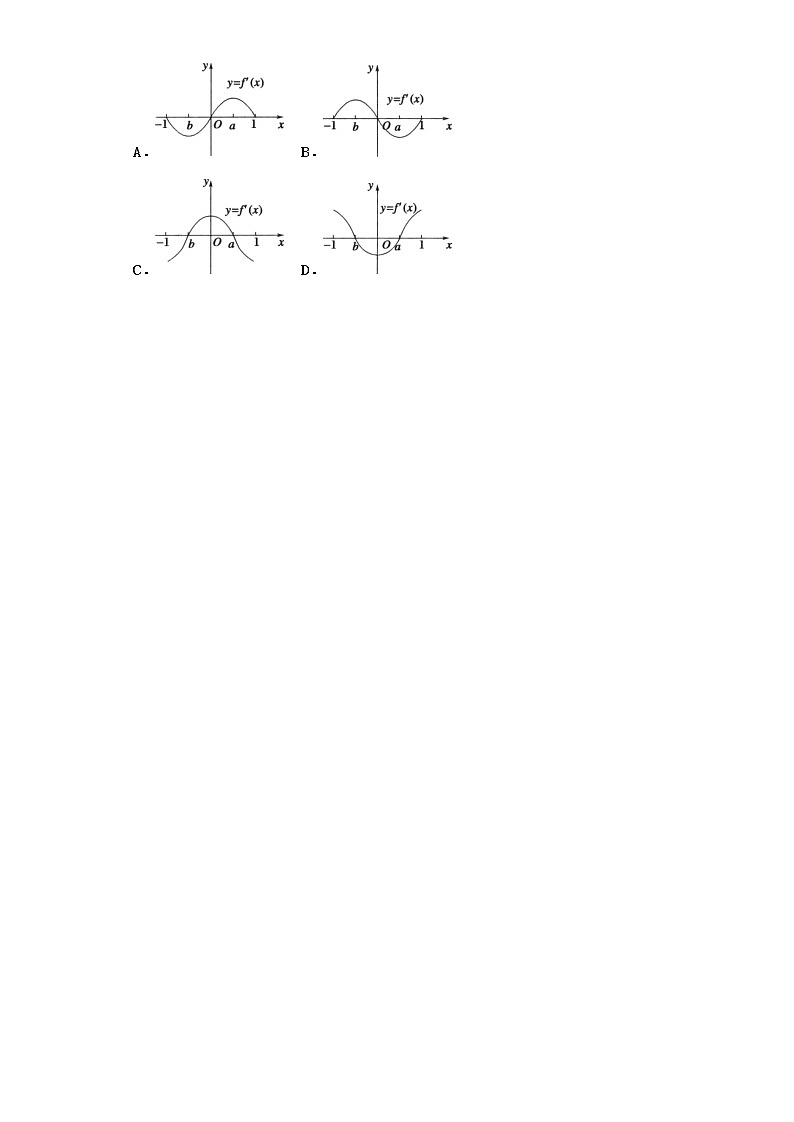
4．

如图所示是函数的导函数的图象，则下列判断中正确的是（    ）

A．函数在区间上是减函数

B．函数在区间上是减函数

C．函数在区间上是减函数

D．函数在区间上是单调函数

5．

函数f(x)＝cos x－x在(0，π)上的单调性是（    ）

A．先增后减 B．先减后增

C．单调递增 D．单调递减

6．

已知定义在R上的函数f(x)满足f(2)=20，且f(x)的导函数满足，则不等式f(x)>2x3+2x的解集为（    ）

A．{x|x>-2} B．{x|x>2} C．{x|x<2} D．{x|x<-2或x>2}

7．

函数满足，在上存在导函数，且在上，若，则实数的取值范围为（    ）

A． B．

C． D．

8．

已知函数的图象如图所示，则函数的图象可能是图中的（    ）

A． B．

C． D．

9．

定义在R上的偶函数，其导函数，当x≥0时，恒有，若，则不等式的解集为（　　）

A．(,1) B．(∞,)∪(1,+∞)

C．(,+∞) D．(∞,)

10．

已知奇函数f（x）的导函数为，当x≠0时，x+f（x）＞0，若a＝f，b＝﹣ef（﹣e），c＝f（1），则a，b，c的大小关系正确的是（    ）

A．a＜b＜c B．b＜c＜a C．a＜c＜b D．c＜a＜b

11．

若函数在区间上单调递增，则实数的取值范围是（    ）

A． B．

C． D．

12．

已知奇函数是定义在R上的可导函数，其导函数为，当时，有，则不等式的解集为（    ）

A． B．

C． D．

13．

如果函数y＝f(x)的图象如图所示，那么导函数y＝的图象可能是（    ）

A． B．

C． D．

14．

定义在R上的可导函数的导数为，满足且是偶函数，（为自然对数的底数），则不等式的解集为（　　）

A． B．

C． D．

15．

已知函数，则不等式的解集是（    ）

A． B． C． D．

参考答案与试题解析

1．【答案】D

【解析】

由题意知：，

的最小值为，是的一个极值点，

，解得：，；

若，当时，，不符合题意．

若，则，当时，；当时，；

在上单调递减，在上单调递增，是的最小值，满足题意；

若，令，解得：或；

当或时，；当时，；

在，上单调递减，在上单调递增，

又，当时，；

是的最小值，满足题意；

综上所述：，.

故选：D.

2．【答案】A

【解析】

令，则

,

由于当时，为上的单调递减函数，

即.

故选：A.

3．【答案】A

【解析】

由题意，设，

则（）．

由已知，

所以当时，，当时，，

又因为在上可导，

故函数在上单调递增，在上单调递减，

所以，所以无解，即方程无解，

即方程无解，所以函数无零点．

故选：A．

4．【答案】A

【解析】

由函数的导函数的图像知，

A：时，，函数单调递减，故A正确；

B：时，或，

所以函数先单调递减，再单调递增，故B错误；

C：时，，函数单调递增，故C错误；

D：时，或，

所以函数先单调递减，再单调递增，不是单调函数，故D错误.

故选：A

5．【答案】D

【解析】

f′(x)＝－sin x－1，x∈(0，π)，

∴f′(x)<0，则f(x)＝cos x－x在(0，π)上单调递减.

故选：D

6．【答案】B

【解析】

令，因，则，即在R上单调递增，

因，则不等式f(x)>2x3+2x等价于，于是得x>2，

所以原不等式的解集为{x|x>2}.

故选：B

7．【答案】D

【解析】

由函数满足，可知函数为奇函数，

，

即，

构造函数，

由题意知：在上，，

故在上单调递减，

为奇函数，

，

即为奇函数，

故在R上单调递减，

因此原不等式可化为：，

即，解得.

故选：D．

8．【答案】C

【解析】

解：由函数的图象的增减变化趋势，判断函数取值的正．负情况如下表：

所以当时，函数的图象在x轴下方；

当时，函数的图象在x轴上方；

当时，函数的图象在x轴下方．

故选：C.

9．【答案】A

【解析】

当时，，又，

∴，即在上单调递减．

∵是定义在R上的偶函数，

∴是定义在R上的偶函数，

由不等式，则有，

∴，解得：．

∴不等式的解集为．

故选：A

10．【答案】C

【解析】

解：令g（x）＝xf（x），则g′（x）＝f（x）+xf′（x）＞0，

所以g（x）为递增函数，

因为e＞1＞，∴g（e）＞g（1）＞g（），

∴ef（e）＞f（1）＞f（），

又f（x）为奇函数，所以﹣ef（﹣e）＝ef（e），

∴b＞c＞a，

故选：C.

11．【答案】C

【解析】

依题意在区间上恒成立，

则，

令，，

即在上递减，所以，

所以.

故选：C

12．【答案】A

【解析】

解：设，由为奇函数，可得，

故为上的奇函数，当时，，

，单调递增，

根据奇函数的对称性可知，在上单调递增，

则不等式可转化为，

即，

即，即．

故选：A

13．【答案】A

【解析】

由原函数的单调性可以得到导函数的正负情况依次是正→负→正→负，只有选项A满足．

故选：A．

14．【答案】C

【解析】

构造函数，所以，

因为，所以，因此函数是实数集上的增函数，

因为函数是偶函数，所以有，

令，有，因此，

于是由，

因为函数是实数集上的增函数，所以有，

故选：C

15．【答案】C

【解析】

的定义域为，由

所以在上递增，又，

所以不等式的解集是．

故选：C.