数学6.2.1导数与函数的单调性一课一练

【特供】6.2.1 导数与函数的单调性-2课时练习

一．填空题

1．

函数与的图像如图所示，则的递增区间是________．

2．

若，函数为增函数，则实数的取值范围为______.

3．

函数在上单调递增，则a的取值范围是________．

4．

设函数，则不等式的解集是_____.

5．

已知定义在R上的函数的导函数为，满足，若恒成立，则实数的取值范围为___________.

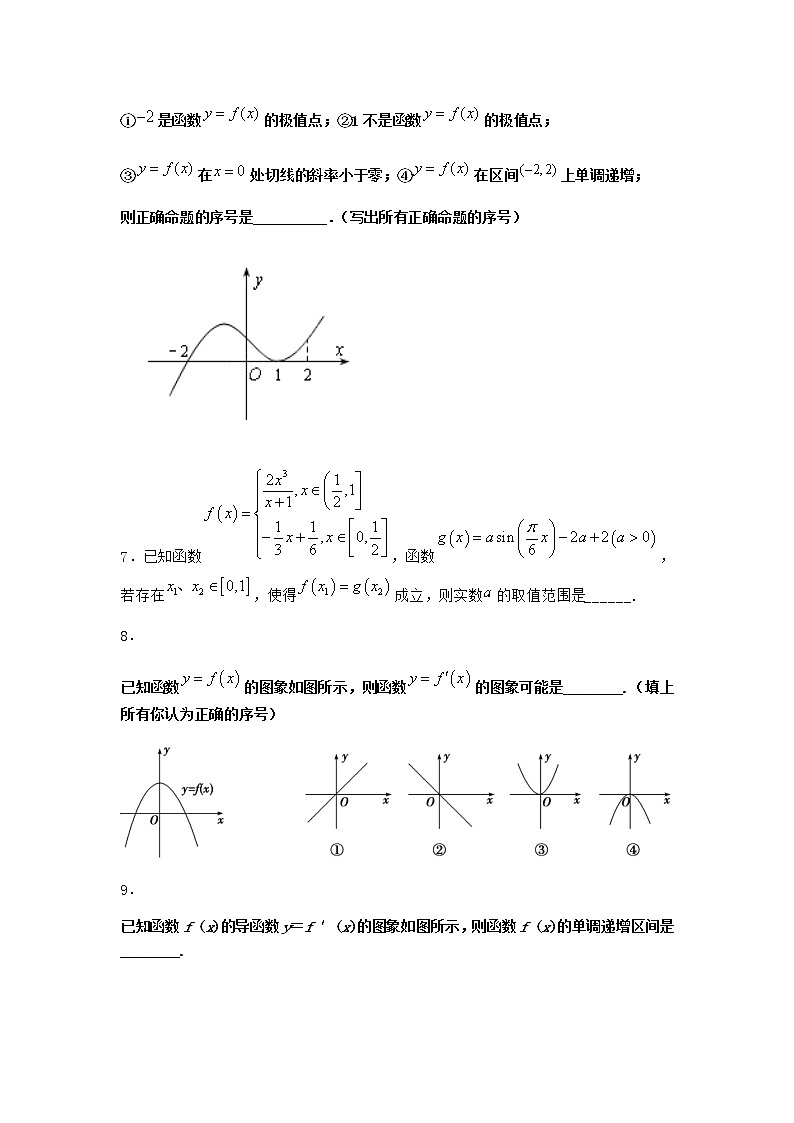
6．

下图是函数的导函数的图象，给出下列命题：

①是函数的极值点；②1不是函数的极值点；

③在处切线的斜率小于零；④在区间上单调递增；

则正确命题的序号是__________．（写出所有正确命题的序号）

7．已知函数，函数，若存在，使得成立，则实数的取值范围是______.

8．

已知函数的图象如图所示，则函数的图象可能是________.（填上所有你认为正确的序号）

9．

已知函数f (x)的导函数y＝f ′(x)的图象如图所示，则函数f (x)的单调递增区间是________.

10．已知，，，则的最大值为_______.

11．

当时，的单调递减区间是___________.

12．

已知定义在上的函数满足，且对于任意的，恒成立，则不等式的解集为________.

13．

若函数的单调递减区间为，则_________．

14．

已知函数，若在上恒成立，则m的最大值为___________.

15．

函数的定义域是，其导函数是，若，则关于x的不等式的解集为___________

参考答案与试题解析

1．【答案】

【解析】

，

令，即，，

由图知：实线为函数的图象，虚线为的图象，

所以当时，，

所以的递增区间是.

故答案为：

2．【答案】

【解析】

为上的增函数，对恒成立，

，，，解得：，

实数的取值范围为.

故答案为：.

3．【答案】

【解析】

函数导数，因为函数在R上是单调递增函数，所以导数，在区间恒成立，

即，即，

，，当时等号成立，，

即，解得：.

故答案为：

4．【答案】

【解析】

解：的定义域为，

因为，

所以为偶函数，

当时，，则，

所以在上为减函数，

所以由，得，得，

解得，

故答案为：

5．【答案】

【解析】

解：令，则，

因为，所以，

所以在R上单调递增，

因为，所以，

所以，

所以，

所以，即在R上恒成立，

所以，解得，

所以实数的取值范围为，

故答案为：

6．【答案】①②④

【解析】

由图象可知：时，，所以在单调递减；

时，，所以在单调递增；且，

所以是函数的极值点，故①正确；②正确

又因为，所以在处切线的斜率，所以③错误；

在区间上单调递增，所以④正确，

故答案为：①②④.

7．【答案】

【解析】分析：根据的范围确定的值域和的值域，根据成立，推出的值域和的值域交集非空，先求二者交集为空集时的取值范围，进而可求交集非空时的取值范围.

详解：当时 ，在上单调递减，

所以，即，，

当时，，

所以，可得在单调递增，

所以，即，

所以的值域为，

因为且 ，

所以，即，

因为，所以，所以

所以的值域为，

因为存在，使得成立，所以，

若，则或，此时或，

所以当时，的取值范围是：.

所以实数的取值范围是，

故答案为：

【点睛】

本题考查了函数的单调性的判断，利用了导数研究函数的单调性，同时考查了利用单调性研究函数的值域问题，属于中档题.

8．【答案】②

【解析】

由函数的图象可知，函数在单调递增，在单调递减，故导函数在区间内有，在区间内有，即导函数的图象可能是选项②.

故答案为②

9．【答案】和

【解析】

由y＝f ′(x)的图象可得当和时，，此时单调递增，

所以函数f (x)的单调递增区间是和.

故答案为：和.

10．【答案】

【解析】分析：依题意可得，从而可得，将化为，令利用基本不等式求出的范围，构造函数，，利用导数研究函数的最值，从而得解；

详解：解：因为，即

所以

所以

令，所以，，

所以，令解得，即在上单调递增，令解得，即在上单调递减，所以

故答案为：

【点睛】

本题考查利用导数研究函数的单调性与最值，考查转化思想，属于中档题.

11．【答案】

【解析】

由题意，函数，可得，

令，即，解得，

所以函数的单调递减区间为.

故答案为：.

12．【答案】.

【解析】

，

设，

则，

是上的减函数，且，

不等式，

即为，

所以，

得，解得或，

原不等式的解集为.

故答案为:.

13．【答案】

【解析】

由题意，所以的两根为和3，

所以，所以，

．

故答案为：．

14．【答案】3

【解析】

，

令，即恒成立，

令，则在上恒成立，

所以在上得到递增，

所以，即，

在上为减函数，

恒成立，

，

最大值为3.

故答案为：3

15．【答案】

【解析】

， ，，

在区间上单调递减，

，

即，

所以不等式的解集是.

故答案为：