小学二 圆柱和圆锥优秀精练

绝密★启用前

2022-2023学年六年级数学下册

第二单元圆柱和圆锥检测卷（A卷˙基础卷）

考试时间：80分钟；满分：102分

班级：            姓名：               成绩:            

注意事项：

1．答题前填写好自己的班级、姓名等信息。

2．请将答案正确填写在答题区域，注意书写工整，格式正确，卷面整洁。

卷面（2分）。我能做到书写工整，格式正确，卷面整洁。

一、知识空格填一填。（每空1分，共20分）

1．沿圆柱的高剪开侧面，侧面是(        )，长方形的长等于圆柱(        )的(        )，长方形的宽等于圆柱的(        )。若沿斜直线剪开，圆柱的侧面是(         )。

2．圆柱的表面积的含义。

圆柱的表面由(        )、(        )组成。

圆柱的表面积＝(        )＋(        )

3．把一个底面半径是10厘米的圆柱侧面展开，得到一个正方形，这个圆柱的高是(        )厘米。

4．一个圆柱的底面周长是9.42分米，高3分米，这个圆柱的侧面积是(        )平方分米。

5．如图是一个长为3cm，宽为2cm的长方形纸片，若将长方形纸片绕长边所在的直线旋转一周，得到的几何体的体积为(        )cm3。（近似值取3）

6．一块圆锥形铁块，底面积是2.7平方厘米，高是5厘米，它的体积是(        )立方厘米。

7．一个圆柱和一个圆锥的体积相等，底面积也相等，圆锥的高是0.6米，圆柱的高是(        )米。

8．把底面半径5厘米、高10厘米的圆柱底面平均分成16份（如图），切开拼成近似的长方体，长方体的长是(        )厘米，宽是(        )厘米，体积是(        )立方厘米。

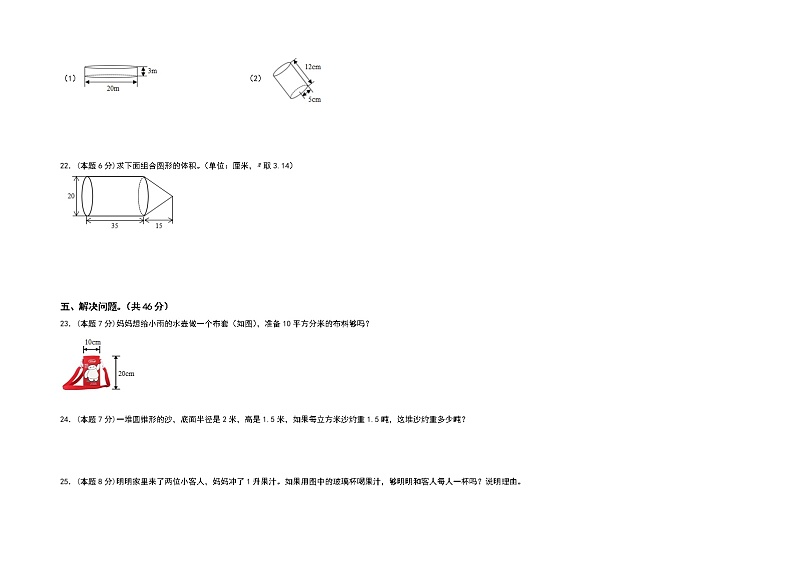
9．有一圆柱形材料，体积约是3.6立方米，每立方米材料约重0.8千克，这个圆柱形材料约重(        )千克。把这个圆柱形材料削成最大的圆锥，重量减少了(        )千克。

10．一个装满水的矿泉水瓶，内直径6cm。凡凡喝了一些。把瓶盖拧紧后倒置放平、无水部分高10cm，凡凡喝了(        )mL的水。

二、是非曲直辩一辩。（对的画√，错的画X，每题2分，共10分）

11．圆锥和圆柱一样，有无数条高。(        )

12．一个圆柱从正面看是一个正方形，这个圆柱的高等于底面直径。(        )

13．长方体、正方体、圆柱和圆锥的体积公式都可以用表示。(        )

14．沿着圆柱的任意一条高把侧面剪开，可以得到一个长方形。(        )

15．圆柱和圆锥底面积和体积都相等，它们高的比是1∶1。(        )

三、众说纷纭选一选。（将正确的选项填在括号内，每题2分，共10分）

16．底面周长和高相等的圆柱，侧面沿高展开后得到的图形是（         ）。

A．长方形 B．正方形 C．平行四边形 D．等腰梯形

17．做一个无盖的圆柱形水桶，求至少需要多少铁皮，就是求水桶的（         ）。

A．底面积 B．侧面积 C．表面积 D．侧面积＋一个底面积

18．把一个圆柱形木头锯成两根，得到的两根圆柱形木头的表面积之和与原来圆柱形木头的表面积相比（         ）。

A．增加了 B．减少了 C．不变 D．无法确定

19．把一个底面半径是2米，高是5米的圆柱沿半径分割成若干等分（如图），拼成一个近似的长方体，表面积增加了（         ）平方米。

A．10 B．20 C．30 D．40

20．把一个的圆柱削成一个最大的圆锥，削去部分的体积是（         ）。

A． B． C． D．

四、巧思妙想算一算。（共14分）

21．(本题8分)求下面各圆柱的表面积。

（1）                   （2）

22．(本题6分)求下面组合图形的体积。（单位：厘米，取3.14）

五、解决问题。（共46分）

23．(本题7分)妈妈想给小雨的水壶做一个布套（如图），准备10平方分米的布料够吗？

24．(本题7分)一堆圆锥形的沙，底面半径是2米，高是1.5米，如果每立方米沙约重1.5吨，这堆沙约重多少吨？

25．(本题8分)明明家里来了两位小客人，妈妈冲了1升果汁。如果用图中的玻璃杯喝果汁，够明明和客人每人一杯吗？说明理由。

26．(本题8分)一堆小麦成圆锥形，占地面积是7.065平方米，高是2米，把这堆小麦装进底面半径是1米的圆柱形粮囤里（厚度忽略不计），可以装多高？

27．(本题8分)陀螺在我国最少有四、五千年的历史，是民间最早的娱乐工具之一。小刚有一个底面直径是6厘米的木制陀螺（如图），这个陀螺的体积是多少立方厘米？

28．(本题8分)一个小圆锥体玩具被芳芳一不小心掉进了一个底面积为3平方分米，高4分米的圆柱体量杯中，她发现正好水面上升了1分米。你能求出这个小圆锥体玩具的体积吗？

答案解析部分

一、知识空格填一填。

1．     长方形     底面     周长     高     平行四边形

【详解】沿圆柱的高剪开侧面，侧面是长方形，长方形的长等于圆柱底面的周长，长方形的宽等于圆柱的高。若沿斜直线剪开，圆柱的侧面是平行四边形。

如图：

2．     一个侧面     两个底面     圆柱的侧面积     两个底面的面积

【分析】圆柱是由3个面围成的，圆柱的上、下两个面叫做底面，圆柱周围的面（上、下底面除外）叫做侧面，那么圆柱的表面积等于上、下两个底面积与侧面积的和，据此解答。

【详解】分析可知，圆柱的表面由一个侧面、两个底面组成，圆柱的表面积＝圆柱的侧面积＋两个底面的面积。

本题主要考查圆柱的表面积，熟记圆柱表面的组成部分是解答题目的关键。

3．62.8

【分析】由一个圆柱的底面半径为10厘米，侧面展开后正好是一个正方形，可得高等于这个圆柱的底面周长，然后用圆的周长公式：C＝，代入数据即可求出这个圆柱的高。

【详解】2×3.14×10＝62.8（厘米）

此题主要考查圆柱的展开图特征以及圆的周长公式的运用。

4．28.26

【分析】圆柱的侧面积＝底面周长×高，据此代入数值进行计算即可。

【详解】9.42×3＝28.26（平方分米）

本题考查圆柱的侧面积，熟记公式是解题的关键。

5．36

【分析】若将长方形纸片绕长边所在的直线旋转一周，可得到一个圆柱，圆柱的底面半径为2cm，高为3cm，再利用圆柱的体积公式：V＝，代入数据即可求出圆柱的体积。

【详解】3×22×3

＝3×4×3

＝36（cm3）

即旋转得到的几何体的体积为36cm3。

本题考查了点、线、面、体的知识，熟记常见平面图形旋转可得到什么立方体是解决本题的关键，另外要掌握圆柱的体积计算公式。

6．4.5

【分析】圆锥的体积＝×底面积×高，把题中数据代入公式计算，据此解答。

【详解】×2.7×5

＝0.9×5

＝4.5（立方厘米）

掌握圆锥的体积计算公式是解答题目的关键。

7．0.2

【分析】由题意可知，圆柱和圆锥的体积相等，底面积也相等，则圆柱的高是圆锥的高的，据此进行计算即可。

【详解】0.6×＝0.2（米）

则圆柱的高是0.2米。

本题考查圆柱和圆锥的体积，明确体积相等，底面积也相等的圆柱的高是圆锥的高的是解题的关键。

8．     15.7     5     785

【分析】把圆柱切成若干等分，拼成一个近似的长方体，这个近似长方体的长等于圆柱底面周长的一半，宽等于圆柱的底面半径，高等于圆柱的高，体积不变，长方体的体积等于圆柱的体积，利用圆柱的体积公式，把数据代入求出圆柱的体积即可，据此解答。

【详解】2×3.14×5÷2

＝6.28×5÷2

＝15.7（厘米）

3.14×52×10

＝3.14×25×10

＝785（立方厘米）

即长方体的长是15.7厘米，宽是5厘米，体积是785立方厘米。

本题重点考查了圆柱体积公式的推导过程，掌握长方体的长、宽、高与圆柱的关系是解题的关键。

9．     2.88     1.92

【分析】用圆柱的体积乘每立方米材料的重量，即可求出这个圆柱形材料的重量；圆柱内最大的圆锥与原来圆柱是等底等高的，所以圆锥的体积是圆柱的体积的，则削去部分的体积是圆柱体积的（1－），据此求出减少部分的体积，再乘每立方米材料的重量，即可解答。

【详解】3.6×0.8＝2.88（千克）

3.6×（1－）×0.8

＝3.6××0.8

＝2.4×0.8

＝1.92（千克）

抓住圆柱内最大圆锥的特点以及等底等高的圆柱的体积与圆锥的体积的倍数关系即可解决此类问题。

10．282.6

【分析】因为原来瓶是装满水的，所以喝的水量就是倒置后无水部分的体积，根据圆柱的容积公式：V＝πr2h，代入数值进行计算即可。

【详解】3.14×（6÷2）2×10

＝3.14×9×10

＝28.26×10

＝282.6（cm3）

＝282.6（mL）

则凡凡喝了282.6mL的水。

本题考查圆柱的容积，熟记公式是解题的关键。

二、是非曲直辩一辩。

11．×

【分析】根据圆柱的高和圆锥高的含义：圆柱的两个底面之间的距离，叫做圆柱的高，圆柱有无数条高；从圆锥的顶点到底面圆心的距离叫做圆锥的高，圆锥的高有1条；进行解答即可。

【详解】由分析可知：

圆柱有无数条高，圆锥只有1条高。所以原题干说法错误。

故答案为：×

明确圆柱的特征和圆柱、圆锥高的含义，是解答此题的关键。

12．√

【分析】先分析出从正面看，看到了圆柱的哪些边，再结合正方形四个边都相等的特征，解题即可。

【详解】圆柱从正面看，看到了它的高和底面直径。那么当它从正面看是一个正方形时，这个圆柱的高等于底面直径。

故答案为：√

本题考查了圆柱，掌握圆柱的特征是解题的关键。

13．×

【分析】长方体、正方体、圆柱体的体积都等于底面积乘高，而圆锥的体积等于底面积乘高再乘，进而得出结论。

【详解】根据分析得，长方体、正方体、圆柱和圆锥的体积公式可表示为：V＝Sh，而圆锥的体积公式表示为：V＝Sh，所以原题的说法是错误的。

故答案为：×

解答此题的关键是根据方体、正方体、圆柱体的体积公式和圆锥的体积计算公式进行解答即可。

14．√

【分析】根据圆柱的侧面展开图，直接判断即可。

【详解】圆柱的侧面展开图是长方形，所以沿着圆柱的任意一条高把侧面剪开，可以得到一个长方形。

故答案为：√

本题考查了圆柱，解题关键是明确圆柱的侧面展开图是长方形。

15．×

【分析】根据圆柱的体积公式：体积＝底面积×高；圆锥的体积公式：体积＝底面积×高×；即可求出圆柱的高与圆锥的高的比。

【详解】设圆柱的底面积为S，高为h1；圆锥的高为h2，则圆锥的底面积是S。

Sh1＝Sh2

h1＝h2

h1∶h2＝1∶3

若一个圆柱和一个圆锥的体积和底面积都相等，则这个圆柱和圆锥高的比是1∶3。

原题干说法错误。

故答案为：×

利用圆柱的体积公式和圆锥的体积公式，以及比的意义进行解答。

三、众说纷纭选一选。

16．B

【分析】圆柱侧面沿高展开后得到图形的长等于底面周长，宽为圆柱的高，当圆柱的底面周长和高相等时，侧面沿高展开后得到的图形的长和宽也是相等的，据此解答。

【详解】底面周长和高相等的圆柱，侧面沿高展开后得到的图形长和宽也是相等的，也就是正方形。

故答案为：B

解答本题的关键是明确圆柱侧面沿高展开后图形的长等于圆柱的底面周长，宽为圆柱的高。

17．D

【分析】根据圆柱的特征可知，圆柱的上、下底面是完全相同的两个圆，侧面是一个曲面。

根据题意可知，这个圆柱形水桶无盖，所以少上底面，求至少需要多少铁皮，就是求这个无盖圆柱形水桶的侧面积和一个底面积的和；据此选择。

【详解】做一个无盖的圆柱形水桶，求至少需要多少铁皮，就是求水桶的侧面积与一个底面积的和。

故答案为：D

本题考查圆柱的表面积公式的灵活运用，在计算圆柱的表面积时，要弄清少了哪个面，要计算哪些面的面积之和。

18．A

【分析】如图：

把一个圆柱形木头锯成两根，得到的两根圆柱形木头的表面积之和与原来圆柱形木头的表面积相比，侧面积不变，多了2个底面的面积，据此解答。

【详解】把一个圆柱形木头锯成两根，得到的两根圆柱形木头的表面积之和与原来圆柱形木头的表面积相比增加了。

故答案为：A

明确平行于圆柱的底面切，切1刀，分成2段，增加2个底面。

19．B

【分析】把圆柱进行切分，然后拼成一个近似的长方体，在这一过程中，体积不发生变化；但拼成的长方体表面积就比圆柱多了两个长方形的面积，这两个长方形的长和圆柱的高相等，宽和圆柱的底面半径相等，由此即可求出增加的表面积。

【详解】5×2×2＝20（平方米）

故答案为：B

抓住圆柱的切割特点，明确体积不变，找出增加的表面积是以底面半径和高为边长的两个长方形的面的面积是解决此类问题的关键。

20．B

【分析】在等底等高的情况下，圆锥的体积是圆柱体积的，把圆柱的体积看作单位“1”，所以削去部分的体积是圆柱体积的（1－），已知圆柱的体积是，求一个数的几分之几是多少，用乘法，即可求出削去部分的体积。

【详解】60×（1－）

＝60×

＝40（cm3）

故答案为：B

此题的解题关键是利用圆锥和圆柱体积之间的关系求解。

四、巧思妙想算一算。

21．（1）816.4m2；（2）533.8cm2

【分析】根据圆柱的表面积公式进行解答即可，圆柱的表面积＝。

【详解】（1）2×3.14×（20÷2）2＋2×3.14×（20÷2）×3

＝6.28×102＋6.28×10×3

＝6.28×100＋62.8×3

＝628＋188.4

＝816.4（m2）

（2）2×3.14×52＋2×3.14×5×12

＝6.28×25＋6.25×5×12

＝157＋31.4×12

＝157＋376.8

＝533.8（cm2）

22．12560立方厘米

【分析】组合图形的体积＝圆柱体积＋圆锥体积，圆柱体积＝底面积×高，圆锥体积＝底面积×高÷3，据此列式计算。

【详解】20÷2＝10（厘米）

3.14×102×35＋3.14×102×15÷3

＝3.14×100×35＋3.14×100×5

＝10990＋1570

＝12560（立方厘米）

五、解决问题。

23．够

【分析】根据圆柱的表面积公式：S表＝S侧＋S底×2，把数据代入公式求出这个圆柱的表面积，然后与10平方分米进行比较即可。

【详解】3.14×10×20＋3.14×（10÷2）2×2

＝31.4×20＋3.14×52×2

＝628＋3.14×25×2

＝628＋157

＝785（平方厘米）

10平方分米＝1000平方厘米

785平方厘米＜1000平方厘米

答：准备10平方分米的布料够。

此题的解题关键是灵活运用圆柱的表面积公式解决实际的问题。

24．9.42吨

【分析】根据圆锥的体积公式：V＝，代入已知的数据，求出这堆圆锥形的沙的体积，再乘每立方米沙的重量，即可求出这堆沙大约的重量。

【详解】×3.14×22×1.5×1.5

＝×1.5×3.14×4×1.5

＝0.5×3.14×4×1.5

＝9.42（吨）

答：这堆沙约重9.42吨。

熟练掌握圆锥的体积公式，是解答此题的关键。

25．够；理由见详解。

【分析】根据题意，圆柱的底面半径为（6÷2）厘米，高为10厘米，利用圆柱的体积（容积）公式：V＝代入即可求出其中1个玻璃杯的容积，再乘3得出3个玻璃杯的容积，换算单位后与1升果汁比较大小，如果小于1升果汁，说明够明明和客人每人一杯，反之则不够明明和客人每人一杯。

【详解】3.14×（6÷2）²×10×3

＝3.14×3²×10×3

＝3.14×9×10×3

＝282.6×3

＝847.8（立方厘米）

847.8立方厘米＝847.8毫升

1升＝1000毫升

847.8毫升＜1升

答：够明明和客人每人一杯。因为果汁的体积大于3个杯子能容纳液体的最大体积。

此题的解题关键是灵活运用圆柱的体积（容积）公式求解。注意换算单位。

26．1.5米

【分析】先根据圆锥的体积公式：V＝Sh，求出小麦的体积，然后用小麦的体积除以圆柱的底面积即可求出高，据此解答。

【详解】

（米）

答：可以装1.5米。

本题主要考查圆锥的体积公式、圆柱的体积公式在实际生活中的应用，解答本题的关键是熟记公式。

27．113.04立方厘米

【分析】由题干可知，圆柱和圆锥是等底的，求圆柱和圆锥的体积之和就是陀螺的体积。分别利用圆柱和圆锥的体积公式求解即可。

【详解】3.14×（6÷2）2×3＋×3.14×（6÷2）2×3

＝3.14×32×3＋×3×3.14×32

＝3.14×9×3＋3.14×9

＝84.78＋28.26

＝113.04（立方厘米）

答：这个陀螺的体积是113.04立方厘米。

此题考查的是圆柱和圆锥的体积公式的应用，熟记公式是解题关键。

28．3立方分米

【分析】小圆锥体玩具的体积等于上升部分水的体积，上升部分水的体积＝量杯的底面积×上升部分水的高度，据此解答。

【详解】3×1＝3（立方分米）

答：这个小圆锥体玩具的体积是3立方分米。

熟记圆柱的体积计算公式并把圆锥体玩具的体积转化为上升部分水的体积是解答题目的关键。