












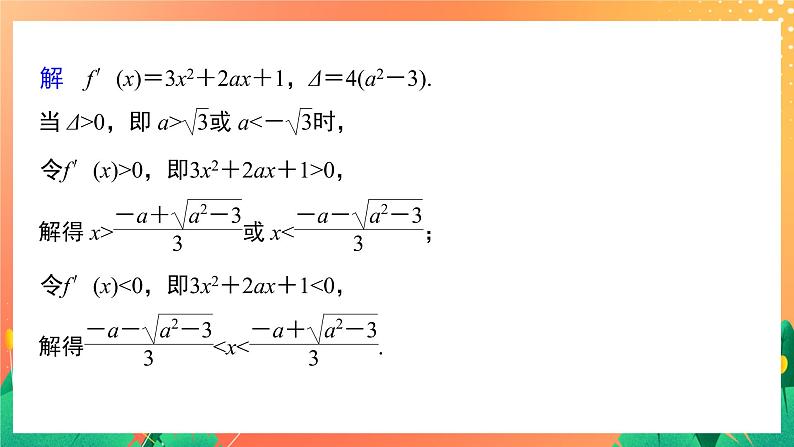






所属成套资源:北师大版数学选择性必修第二册多课时课件PPT(送学案)全套
高中数学北师大版 (2019)选择性必修 第二册6.1 函数的单调性优秀课件ppt
展开
这是一份高中数学北师大版 (2019)选择性必修 第二册6.1 函数的单调性优秀课件ppt,文件包含§661第2课时函数单调性的综合问题课件pptx、§661第1课时导数与函数的单调性课件pptx、§661第1课时导数与函数的单调性教案docx、§661第2课时函数单调性的综合问题教案docx等4份课件配套教学资源,其中PPT共108页, 欢迎下载使用。
1.理解导数与函数的单调性的关系.2.掌握利用导数判断函数单调性的方法.3.能利用导数求不超过三次多项式函数的单调区间.
研究股票时,我们最关心的是股票的发展趋势(走高或走低)以及股票价格的变化范围(封顶或保底).从股票走势曲线图来看,股票有升有降.在数学上,函数曲线也有升有降,就是我们常说的单调性.那么,函数的单调性与导数有什么关系呢?
一、导数与函数单调性的关系
二、判断或证明函数的单调性
问题 已知函数:(1)y=2x-1,(2)y=-3x,(3)y=2x,它们的导数的正负与它们的单调性之间有怎样的关系?
提示 (1)y′=2>0,y=2x-1是增函数.(2)y′=-30,y=2x是增函数.
导数的符号与函数单调性之间的关系
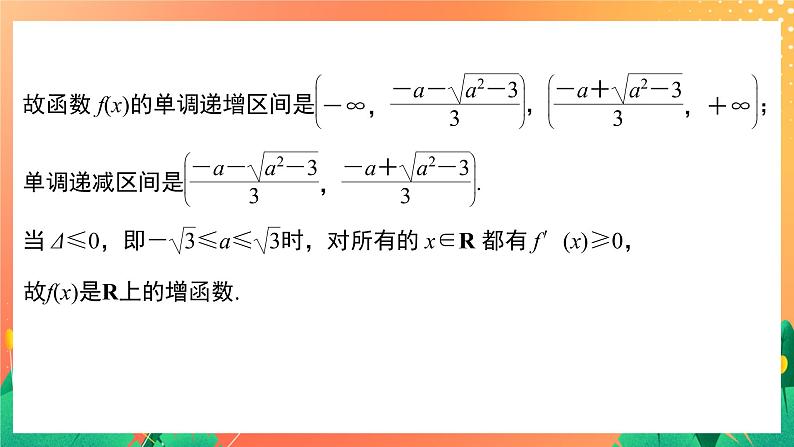
若在某个区间内,f′(x)≥0,且只在有限个点为0,则在这个区间内,函数y=f(x)单调递增;若在某个区间内,f′(x)≤0,且只在有限个点为0,则在这个区间内,函数y=f(x)单调递减.
注意点:“在某区间内f′(x)>0(f′(x)0.
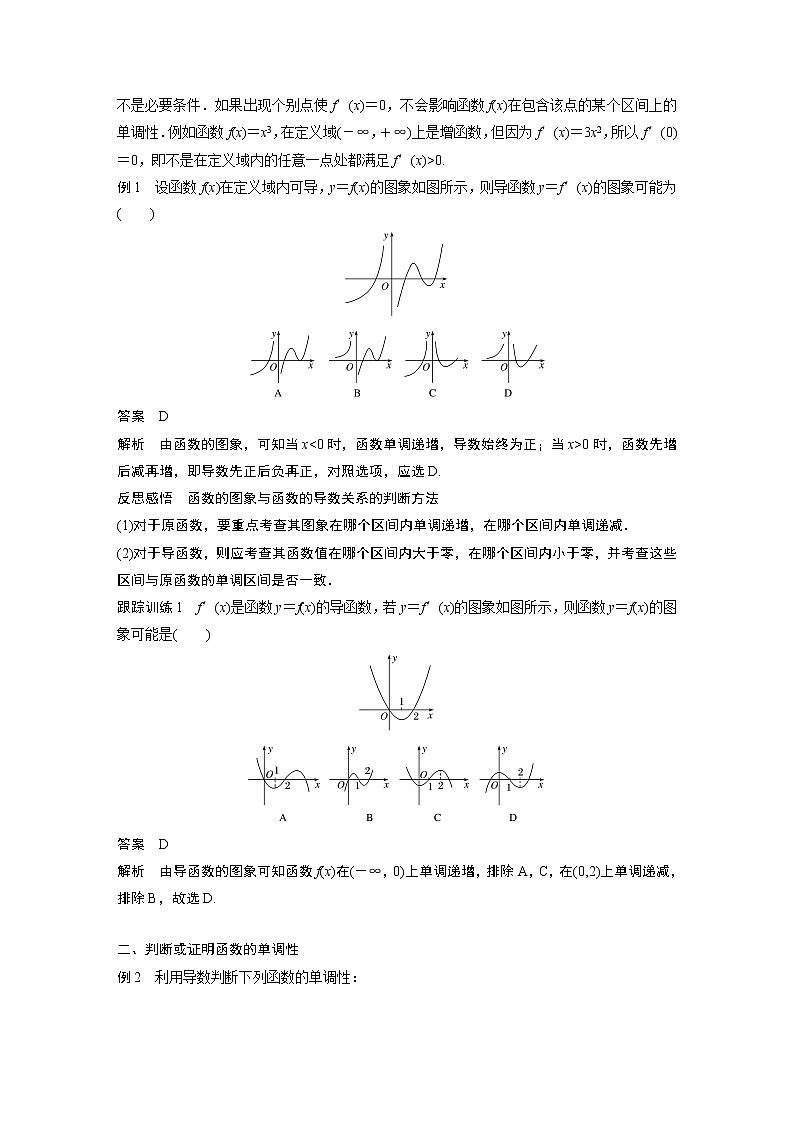
例1 设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为
解析 由函数的图象,可知当x0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.
反思感悟 函数的图象与函数的导数关系的判断方法(1)对于原函数,要重点考查其图象在哪个区间内单调递增,在哪个区间内单调递减.(2)对于导函数,则应考查其函数值在哪个区间内大于零,在哪个区间内小于零,并考查这些区间与原函数的单调区间是否一致.
跟踪训练1 f′(x)是函数y=f(x)的导函数,若y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是
解析 由导函数的图象可知函数f(x)在(-∞,0)上单调递增,排除A,C,在(0,2)上单调递减,排除B,故选D.
例2 利用导数判断下列函数的单调性:
所以f′(x)=x2-2x+2=(x-1)2+1>0,
(3)f(x)=x-ex(x>0).
解 因为f(x)=x-ex,x∈(0,+∞),所以f′(x)=1-ex0(f′(x)
相关课件
这是一份高中数学北师大版 (2019)选择性必修 第二册6.1 函数的单调性图文ppt课件,共15页。PPT课件主要包含了图像法,定义法,作差变形,变形为,函数的平均变化率,函数的瞬时变化率,求定义域,求导数等内容,欢迎下载使用。
这是一份数学必修 第一册3.1.2 函数的单调性优质课ppt课件,文件包含312《函数的单调性》第2课时课件pptx、312《函数的单调性》第2课时教案docx等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
这是一份高中数学6.1 函数的单调性试讲课课件ppt,共32页。PPT课件主要包含了答案D,答案B,1+∞,答案A,答案C,-∞-1等内容,欢迎下载使用。









