









所属成套资源:沪科版数学七年级下学期PPT课件(送教学设计+同步练习)整册
- 9.2.2分式的加减(课件+教案+练习) 课件 7 次下载
- 9.2.3分式的加减(课件+教案+练习) 课件 6 次下载
- 9.3.2分式方程(课件+教案+练习) 课件 6 次下载
- 10.1相交线(课件+教案+练习) 课件 5 次下载
- 10.2.1平行线的判定(课件+教案+练习) 课件 5 次下载
数学七年级下册9.3 分式方程优质ppt课件
展开这是一份数学七年级下册9.3 分式方程优质ppt课件,文件包含931分式方程课件pptx、931分式方程教学设计docx、931分式方程练习题docx等3份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
沪科版数学七年级下9.3.1分式方程教学设计
课题 | 分式方程 | 单元 | 9 | 学科 | 数学 | 年级 | 七 |
学习 目标 | 知识与技能目标 1.理解分式方程的意义. 2.了解解分式方程的基本思路和解法. 3.理解解分式方程时可能无解的原因,并掌握分式方程的验根方法 过程与方法目标 经历“实际问题——分式方程——整式方程”的过程,发展学生分析问题、解决问题的能力,渗透数学的转化思想,培养学生的应用意识 情感态度与价值观目标 在活动中培养学生乐于探究、合作学习的习惯,培养学生努力寻找解决问题的进取心,体会数学的应用价值. | ||||||
重点 | 解分式方程的基本思路和解法 | ||||||
难点 | 理解解分式方程时可能无解的原因. | ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
导入新课 | 师:什么叫做一元一次方程? 生:含有一个未知数,并且未知数的次数是1的方程是一元一次方程. 师:下列方程哪些是一元一次方程? 课件展示:
|
学生思考问题
|
复习以前的知识引入新课,提高学生学习的积极性. |
讲授新课 | 课件展示: 为了满足经济高速发展的需求,我国铁路部门不断进行技术革新,提高列车运行速度。在相距1600km的两地之间运行一列车,速度提高25%后,运行时间缩短了4h,你能求出列车提速前的速度吗? 师:什么是分式方程? 生:分母中含未知数的方程叫做分式方程 师:以前学过的分母里不含有未知数的方程叫做整式方程. 课件展示: 下列方程中,哪些是分式方程?哪些整式方程.
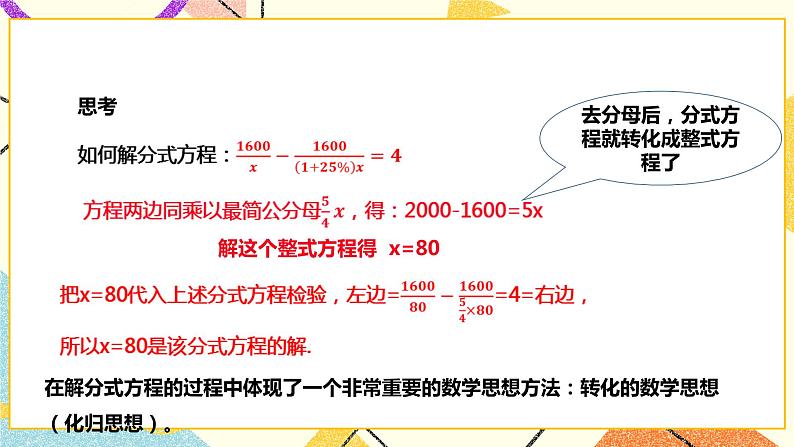
分式方程: 整式方程: 课件展示: 思考 如何解分式方程: 课件展示: 方程两边同乘以最简公分母,得:2000-1600=5x 解这个整式方程得 x=80 把x=80代入上述分式方程检验,左边==4=右边,所以x=80是该分式方程的解. 师:在解分式方程的过程中体现了一个非常重要的数学思想方法:转化的数学思想(化归思想) 师:解方程,把解得的根代入原方程中检验,你发现了什么? 生:解方程 可得 x=3 师:把x=3代入检验时,方程中分式的分母为零,分式无意义,所以x=3不是原方程的根,原方程无解. 师:为什么会产生这种结果呢? 师:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.这就是增根 生:使分母为零的根 师:产生的原因是什么呢? 生:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根. 课件展示: 例1 解方程 师:解分式方程的思路是什么? 生: 注意:验根时,只要把求得的根代入最简公分母,看它的值是否为零,使它不为零的根才是原方程的根,为零的根即为增根,应舍去. 师:由以上解方程的过程,你能总结出解分式方程的步骤吗? 生: 1.在方程的两边都乘以最简公分母,约去分母,化成整式方程; 2.解这个整式方程; 3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去; 4.写出原方程的根.
|
学生设未知数列出方程,通过观察总结出分式方程的概念.
学生解答,老师给予订正
师生共同解分式方程
学生解分式方程,教师给予引导得出增根的定义以及产生增根的原因.
学生解答,并总结出解分式方程的思路.
师生共同总结解分式方程的步骤. |
学生通过解决问题,激发学习的积极性,更好的进入课堂.
巩固分式方程的概念
学生通过自己解决问题,充分发挥学习的主动性,同时也培养了学生归纳问题的能力。
让学生体验学有所用,提高学习的兴趣
培养学生发现规律的能力.
充分发挥学习的主动性,同时也培养了学生归纳问题的能力 |
课堂练习 | 1. 下列说法中,错误的是 ( ) A.分式方程的解等于0,就说明这个分式方程无解 B.解分式方程的基本思路是把分式方程转化为整式方程 C.检验是解分式方程必不可少的步骤 D.能使分式方程的最简公分母等于零的未知数的值不是原分式方程的解 答案:A 2.分式方程的解是( ) A.x=﹣1 B.x=1 C.x=2 D.x=3 答案:D 3.对分式方程 去分母时,应在方程两边都乘以 . 答案: (x+1)(x-1) 4.解方程: 答案: 解:去分母得:2x﹣2=x+3, 解得:x=5, 经检验x=5是分式方程的解. 拓展提高 当m为何值时,方程 会产生增根. 答案: 解:方程两边同乘以最简公分母(x-3),得 x-2(x-3)=m x-2x+6=m 解方程得 : x=6-m 因为原分式方程有增根,所以x=3 得 6-m=3,即 m=3. 中考链接 1.(枣庄中考)关于x的分式方程的解为正数,则字母a的取值范围为( ) A.a≥-1 B.a>-1 C.a≤-1 D.a<-1 答案:B 2.(湖北中考)分式方程 的解 是 . 答案:15 |
学生自主解答,教师讲解答案。
学生自主解答,教师讲解答案。
练中考题型 |
通过这几道题目来反馈学生对本节所学知识的掌握程度,落实基础。学生刚刚接触到新的知识需要一个过程,也就是对新知识从不熟悉到熟练的过程,无论是基础的习题,还是变式强化,都要以学生理解透彻为最终目标。
可以照顾不层次的学生,调动学生学习积极性。
让学生更早的接触中考题型,熟悉考点. |
课堂小结 | 学生归纳本节所学知识 | 回顾学过的知识,总结本节内容,提高学生的归纳以及语言表达能力。 | |
板书 | 1.分式方程:分母里含有未知数的方程 2.解分式方程的思路: 3.解分式方程的步骤: 在方程的两边都乘以最简公分母,约去分母,化成整式方程;解这个整式方程; 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去; 写出原方程的根. |
|
|
相关课件
这是一份初中数学北师大版八年级下册4 分式方程示范课课件ppt,文件包含54分式方程课件pptx、54分式方程练习doc、54分式方程教案doc、54分式方程学案doc等4份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
这是一份沪科版七年级下册第9章 分式9.3 分式方程习题ppt课件,共33页。PPT课件主要包含了答案显示,核心必知,零验根,未知数,k<4且k≠0,或-2,见习题,解分式方程,答案D等内容,欢迎下载使用。
这是一份初中数学沪科版七年级下册第9章 分式9.3 分式方程习题ppt课件,共15页。PPT课件主要包含了答案呈现等内容,欢迎下载使用。









