2023年中考数学一轮复习《菱形》课时练习（含答案）

这是一份2023年中考数学一轮复习《菱形》课时练习（含答案），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
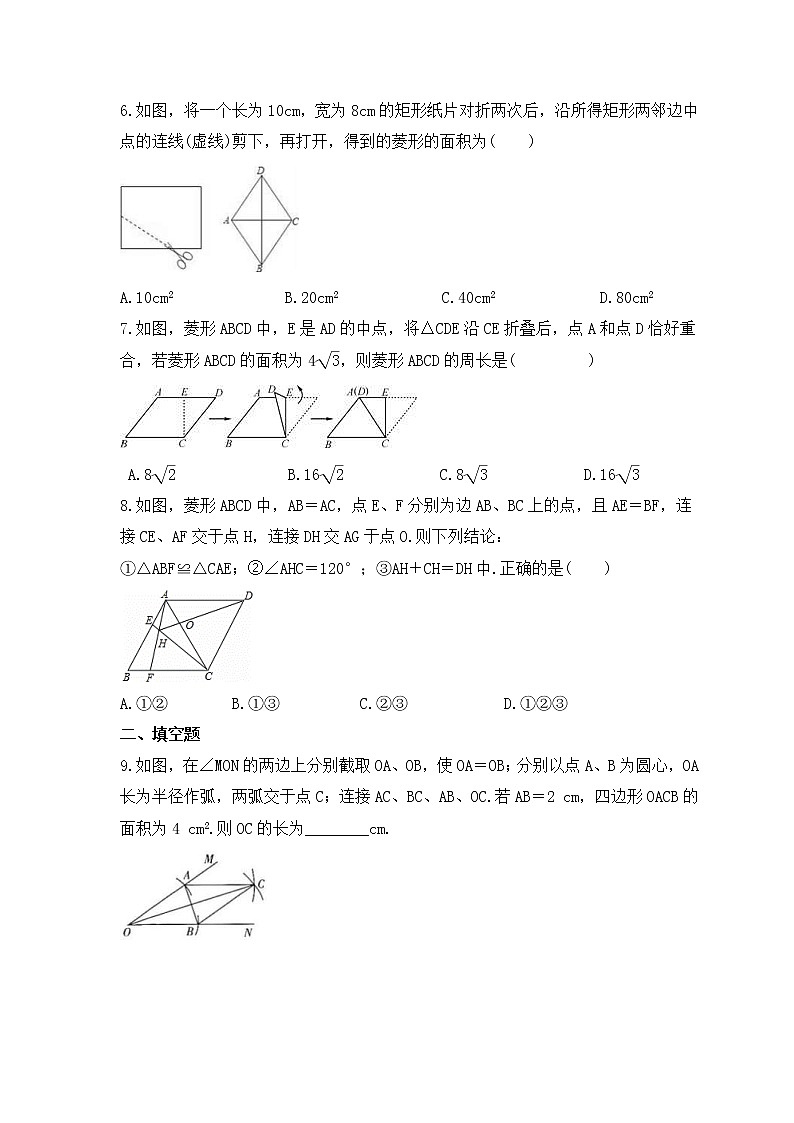
2023年中考数学一轮复习《菱形》课时练习一              、选择题1.能判定一个四边形是菱形的条件是（     ）A.对角线互相平分且相等B.对角线互相垂直且相等C.对角线互相垂直且对角相等D.对角线互相垂直，且一条对角线平分一组对角2.如图，丝带重叠的部分一定是（　　）A.正方形                      B.矩形                    C.菱形      D.都有可能3.下列说法中正确的是（  ）  A.四边相等的四边形是菱形  B.一组对边相等，另一组对边平行的四边形是菱形  C.对角线互相垂直的四边形是菱形  D.对角线互相平分的四边形是菱形4.如图，在菱形ABCD中，BE⊥AD，BF⊥CD，E、F 为垂足，AE＝ED ，则∠EBF等于(       ) A.75°        B.60°           C.50°           D.45° 5.如图，已知菱形ABCD中，对角线AC与BD相交于点O，OE∥DC交BC于点E，AD＝10cm，则OE的长为(　　)A.6cm          B.5cm        C.4cm        D.3cm6.如图，将一个长为10cm，宽为8cm的矩形纸片对折两次后，沿所得矩形两邻边中点的连线(虚线)剪下，再打开，得到的菱形的面积为(　　)A.10cm2         B.20cm2        C.40cm2        D.80cm27.如图，菱形ABCD中，E是AD的中点，将△CDE沿CE折叠后，点A和点D恰好重合，若菱形ABCD的面积为4，则菱形ABCD的周长是(　　     ) A.8        B.16           C.8       D.168.如图，菱形ABCD中，AB＝AC，点E、F分别为边AB、BC上的点，且AE＝BF，连接CE、AF交于点H，连接DH交AG于点O.则下列结论：①△ABF≌△CAE；②∠AHC＝120°；③AH＋CH＝DH中.正确的是(    )A.①②        B.①③          C.②③            D.①②③二              、填空题9.如图，在∠MON的两边上分别截取OA、OB，使OA＝OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC.若AB＝2 cm，四边形OACB的面积为4 cm2.则OC的长为________cm.  10.如图，在菱形ABCD中，∠BAD=80º，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于            ．11.一个菱形的周长为52cm，一条对角线长为10cm，则其面积为　　cm2．12.两对角线分别是6cm和8cm的菱形面积是　　   cm2，周长是　　   cm．13.如图，四边形ABCD和CEFG都是菱形，连接AG，GE，AE，若∠F＝60°，EF＝4，则△AEG面积为________.14.如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB＝90°，∠BAC＝30°.给出下列结论：①EF⊥AC；②四边形ADFE为菱形；③AD＝4AG；④FH＝BD.其中正确的结论为________(请将所有正确的序号都填上).      三              、解答题15.如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，连接BE.（1）求证：四边形BCDE为菱形；（2）连接AC，若AC平分∠BAD，判断AC与CD的数量关系和位置关系，并说明理由.     16.准备一张矩形纸片，按如图操作：将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．(1)求证：四边形BFDE是平行四边形；(2)若四边形BFDE是菱形，AB＝2，求菱形BFDE的面积．          17.(1)如图,纸片▱ABCD中,AD=5,S▱ABCD=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为(　　)A.平行四边形　　B.菱形　　C.矩形　　D.正方形(2)如图,在(1)中的四边形纸片AEE/D中,在EE/上取一点F,使EF=4,剪下△AEF,将它平移至△DE/F/的位置,拼成四边形AFF/D.①求证:四边形AFF'D是菱形;②求四边形AFF'D的两条对角线的长.图1　　　　　　　　　图2      18.如图，在矩形ABCD中，点E为CD上一点，将△BCE沿BE翻折后点C恰好落在AD边上的点F处，将线段EF绕点F旋转，使点E落在BE上的点G处，连接CG.(1)证明：四边形CEFG是菱形；(2)若AB＝8，BC＝10，求四边形CEFG的面积；(3)试探究当线段AB与BC满足什么数量关系时，BG＝CG，请写出你的探究过程．
参考答案1.C2.C.3.B4.B.5.B6.A7.A8.D9.答案为：4.10.答案为：60度  11.答案为：120．12.答案为：24，20．13.答案为：4. 14.答案为：①③④；15. 16.证明：(1)∵四边形ABCD是矩形，∴∠A＝∠C＝90°，AB＝CD，AB∥CD，∴∠ABD＝∠CDB，∴∠EBD＝∠FDB，∴EB∥DF，∵ED∥BF，∴四边形BFDE为平行四边形．(2)∵四边形BFDE为菱形，∴BE＝ED，∠EBD＝∠FBD＝∠ABE，∵四边形ABCD是矩形，∴AD＝BC，∠ABC＝90°，∴∠ABE＝30°，∵∠A＝90°，AB＝2，∴AE＝，BF＝BE＝2AE＝，∴菱形BFDE的面积为：×2＝.17.解：(1)C.(2)①证明:∵AD=BC=5,S▱ABCD=15,AE⊥BC,∴AE=3.如图,∵EF=4,∴在Rt△AEF中,AF=5.∴AF=AD=5.又△AEF经平移得到△DE'F',∴AF∥DF',AF=DF',∴四边形AFF'D是平行四边形.又AF=AD,∴四边形AFF'D是菱形.②如图,连接AF',DF.在Rt△DE'F中,∵E'F=E'E-EF=5-4=1,DE'=3,∴DF=.在Rt△AEF'中,∵EF'=E'E+E'F'=5+4=9,AE=3,∴AF'=3.∴四边形AFF'D的两条对角线长分别为,3. 18.证明：(1)根据翻折的方法可得EF＝EC，∠FEG＝∠CEG.又∵GE＝GE，∴△EFG≌△ECG.∴FG＝GC.∵线段FG是由EF绕F旋转得到的，∴EF＝FG.∴EF＝EC＝FG＝GC.∴四边形FGCE是菱形．(2)连接FC交GE于O点．根据折叠可得BF＝BC＝10.∵AB＝8∴在Rt△ABF中，根据勾股定理得AF＝6.∴FD＝AD－AF＝10－6＝4.设EC＝x，则DE＝8－x，EF＝x，在Rt△FDE中，FD2＋DE2＝EF2，即42＋(8﹣x)2＝x2.解得x＝5.即CE＝5.S菱形CEFG＝CE·FD＝5×4＝20.(3)当＝时，BG＝CG，理由：由折叠可得BF＝BC，∠FBE＝∠CBE，∵在Rt△ABF中，∴BF＝2AF.∴∠ABF＝30°.又∵∠ABC＝90°，∴∠FBE＝∠CBE＝30°，EC＝BE.∵∠BCE＝90°，∴∠BEC＝60°.又∵GC＝CE，∴△GCE为等边三角形．∴GE＝CG＝CE＝BE.∴G为BE的中点．∴CG＝BG＝BE.