

2022-2023学年贵州省遵义市七年级下册数学第一次月考模拟卷(AB卷)含解析
展开
这是一份2022-2023学年贵州省遵义市七年级下册数学第一次月考模拟卷(AB卷)含解析,共43页。试卷主要包含了 在下列实数中,无理数是,2020020002, 下列计算或判断, 的平方根是等内容,欢迎下载使用。
2022-2023学年贵州省遵义市七年级下册数学第一次月考模拟卷(A卷)
一.选一选(共12小题)
1. 如图,已知直线、被直线所截,,E是直线右边任意一点(点E没有在直线,上),设,.下列各式:①,②,③,④,的度数可能是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
2. 如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
A. 76° B. 78° C. 80° D. 82°
3. 四条直线相交于一点,总共有对顶角( )
A. 8对 B. 10对 C. 4对 D. 12对
4. 在同一平面内,有8条互没有重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是( )
A 平行 B. 垂直 C. 平行或垂直 D. 无法确定
5. 在下列实数中,无理数是( )
A. B. C. D. 0.2020020002
6. 下列计算或判断:(1)±3是27立方根;(2)=a;(3)的平方根是2;(4)=±8;(5) =,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
7. 的平方根是( )
A. -2 B. C. D.
8. 实数a,b在数轴上的位置如图所示,下列各式正确的是( )
A. a>0 B. a+b>0 C. a﹣b>0 D. ab<0
9. 如图,A、B、C三点在数轴上所表示的数分别为a、b、c,根据图中各点位置,下列各式正确的是
A. B. C. D.
10. 如图,已知AB∥CD,AD∥BC,∠ABE是平角,则下列说法中正确的是( )
A. ∠1+∠2=∠3 B. ∠1=∠2>∠3 C. ∠1+∠2<∠3 D. ∠1+∠2与∠3的大小没有关系
11. 如图,AB∥CD,用含∠1,∠2,∠3的式子表示∠4,则∠4的值为( )
A. ∠1+∠2﹣∠3 B. ∠1+∠3﹣∠2 C. 180°+∠3﹣∠1﹣∠2 D. ∠2+∠3﹣∠1﹣180°
12. 设的小数部分为b,那么(4+b)b的值是( )
A. 1 B. 是一个有理数 C. 3 D. 无法确定
二.填 空 题(共4小题)
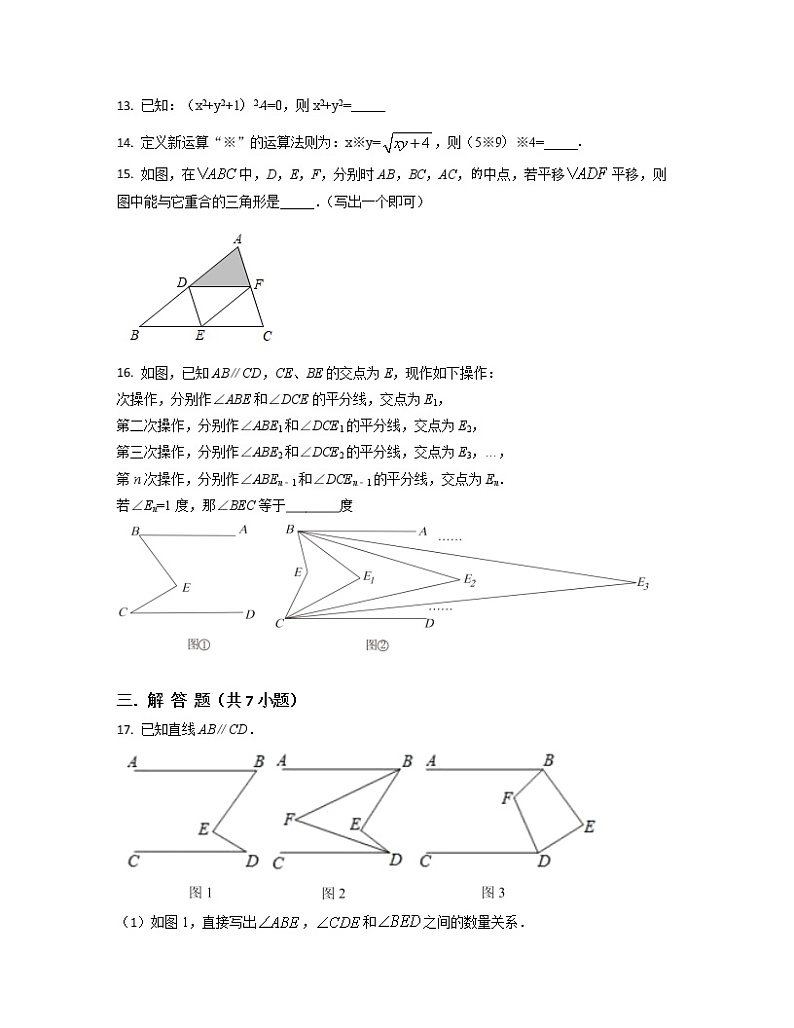
13. 已知:(x2+y2+1)2﹣4=0,则x2+y2=_____
14. 定义新运算“※”的运算法则为:x※y=,则(5※9)※4=_____.
15. 如图,在中,D,E,F,分别时AB,BC,AC,中点,若平移平移,则图中能与它重合的三角形是_____.(写出一个即可)
16. 如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于________度
三.解 答 题(共7小题)
17. 已知直线AB∥CD.
(1)如图1,直接写出,和之间的数量关系.
(2)如图2,,分别平分,,那么和有怎样的数量关系?请说明理由.
(3)若点E位置如图3所示,,仍分别平分,,请直接写出和的数量关系.
18. 如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若没有变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若没有存在,说明理由.
19. 计算:(﹣)2﹣ ﹣+82.
20. 已知m是的整数部分,n是的小数部分,求的值.
21. 阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限没有循环小数,因此 的小数部分我们没有可能全部写出来,于是小明用-1来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<<3,∴ 的整数部分为2,小数部分为 ﹣2.
请解答:
(1)的整数部分是________,小数部分是________.
(2)如果的小数部分为a,的整数部分为b,求a+b- 的值;
(3)已知:x是3+ 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
22. 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)在图中画出△A′B′C′,并写出点A′、B′、C′的坐标;
(2)在y轴上求点P,使得△BCP与△ABC面积相等.
23. 如图,已知AM//BN,,点是射线上一动点(与点没有重合),、分别平分和,分别交射线于、.
(1)求的度数;
(2)在点P的运动过程中,∠APB与∠ADB之间的数量关系是否随之发生变化?若没有变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC度数是 ,并说明理由.
2022-2023学年贵州省遵义市七年级下册数学第一次月考模拟卷(A卷)
一.选一选(共12小题)
1. 如图,已知直线、被直线所截,,E是直线右边任意一点(点E没有在直线,上),设,.下列各式:①,②,③,④,的度数可能是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【正确答案】A
【分析】根据点E有3种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.
【详解】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)当点E在CD的下方时,同理可得,∠AEC=α-β.
综上所述,∠AEC的度数可能为β-α,α+β,α-β.
即①α+β,②α-β,③β-α,都成立.
故选A.
本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等;两直线平行,内错角相等.
2. 如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
A. 76° B. 78° C. 80° D. 82°
【正确答案】B
【详解】如图,分别过K、H作AB的平行线MN和RS,
∵AB∥CD,
∴AB∥CD∥RS∥MN,
∴∠RHB=∠ABE=∠ABK,∠SHC=∠DCF=∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,
∴∠BHC=180°﹣∠RHB﹣∠SHC=180°﹣(∠ABK+∠DCK),
∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK﹣180°,
∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC,
又∠BKC﹣∠BHC=27°,
∴∠BHC=∠BKC﹣27°,
∴∠BKC=180°﹣2(∠BKC﹣27°),
∴∠BKC=78°,
故选B.
3. 四条直线相交于一点,总共有对顶角( )
A. 8对 B. 10对 C. 4对 D. 12对
【正确答案】D
【详解】如图所示,共有12对,故选D.
4. 在同一平面内,有8条互没有重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
【正确答案】A
【详解】∵l2∥l3,l3⊥l4,l4∥l5,l5⊥l6,l6∥l7,l7⊥l8,
∴l2⊥l4,l4⊥l6,l6⊥l8,
∴l2⊥l8.
∵l1⊥l2,
∴l1∥l8.
故选A.
5. 在下列实数中,无理数是( )
A. B. C. D. 0.2020020002
【正确答案】C
【分析】根据无理数的三种形式求解.
【详解】为无理数, 、、0.2020020002为有理数.故选C.
本题考查了无理数知识,解答本题的关键是掌握无理数的三种形式:①开方开没有尽得到的数,②无限没有循环小数,③含有π的数.
6. 下列计算或判断:(1)±3是27的立方根;(2)=a;(3)的平方根是2;(4)=±8;(5) =,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【正确答案】B
【详解】根据立方根的意义,可知27的立方根是3,故(1)没有正确;正确,故(2)正确;由=8,可知其平方根为±,故(3)没有正确;根据算术平方根的意义,可知,故(4)没有正确;根据分母有理化的意义,可知,故(5)正确.
故选B.
7. 的平方根是( )
A -2 B. C. D.
【正确答案】D
【分析】先计算的结果,然后对所得的数求平方根,即可得到答案.
【详解】,
2的平方根为,
故选D.
先对原数进行计算是解决本题的关键.
8. 实数a,b在数轴上的位置如图所示,下列各式正确的是( )
A. a>0 B. a+b>0 C. a﹣b>0 D. ab<0
【正确答案】D
【详解】由数轴可知:a<0<b,|a|>|b|,
∴a+b<0,a﹣b<0,ab<0,
∴选项D正确.
故选D.
9. 如图,A、B、C三点在数轴上所表示的数分别为a、b、c,根据图中各点位置,下列各式正确的是
A. B. C. D.
【正确答案】D
【分析】根据数轴得出c<﹣1<0<a<1<b,求出a﹣1<0,b﹣1>0,c﹣1<0,a+1>0,b+1>0,c+1<0,再根据有理数的运算法则判断即可.
【详解】解:∵从数轴可知:c<﹣1<0<a<1<b,
∴a﹣1<0,b﹣1>0,c﹣1<0,a+1>0,b+1>0,c+1<0,
∴(a﹣1)(b﹣1)<0,(c﹣1)(b﹣1)<0,(a+1)(b+1)>0,(c+1)(b+1)<0,
∴只有选项D正确;选项A、B、C都错误,
故选D.
本题考查了数轴和有理数的运算法则,能根据数轴得出c<﹣1<0<a<1<b是解此题的关键.
10. 如图,已知AB∥CD,AD∥BC,∠ABE是平角,则下列说法中正确的是( )
A. ∠1+∠2=∠3 B. ∠1=∠2>∠3 C. ∠1+∠2<∠3 D. ∠1+∠2与∠3的大小没有关系
【正确答案】A
【详解】∵AB∥CD,AD∥BC,
∴∠1=∠ACB,∠4=∠2,
∵∠CBE=∠4+∠ACB,
∴∠3=∠1+∠2,
∵∠1≠∠2且∠2<∠3,
故选项B,C,D错误,选项A正确,
故选A.
11. 如图,AB∥CD,用含∠1,∠2,∠3的式子表示∠4,则∠4的值为( )
A. ∠1+∠2﹣∠3 B. ∠1+∠3﹣∠2 C. 180°+∠3﹣∠1﹣∠2 D. ∠2+∠3﹣∠1﹣180°
【正确答案】D
【详解】试题解析:过点E作EG∥AB,过点F作FH∥CD,
∵AB∥CD,
∴AB∥CD∥EG∥FH,
∴∠1=∠AEG,
∴∠GEF=∠2-∠1,
∵EG∥FH,
∴∠EFH=180°-∠GEF=180°-(∠2-∠1)=180°-∠2+∠1,
∴∠CFH=∠3-∠EFH=∠3-(180°-∠2+∠1)=∠3+∠2-∠2-180°,
∵FH∥CD,
∴∠4=∠3+∠2-∠1-180°,
故选D.
12. 设的小数部分为b,那么(4+b)b的值是( )
A. 1 B. 是一个有理数 C. 3 D. 无法确定
【正确答案】C
【详解】试题解析:∵的小数部分为b,
∴b=-2,
把b=-2代入式子(4+b)b中,
原式=(4+b)b=(4+-2)×(-2)=3.
故选C.
考点:估算无理数的大小.
二.填 空 题(共4小题)
13. 已知:(x2+y2+1)2﹣4=0,则x2+y2=_____
【正确答案】1.
【详解】∵(x2+y2+1)2﹣4=0,
∴(x2+y2+1)2=4,
∵x2+y2+1>0,
∴x2+y2+1=2,
∴x2+y2=1.
故答案为1.
14. 定义新运算“※”的运算法则为:x※y=,则(5※9)※4=_____.
【正确答案】4.
【详解】5※9=,7※4=,故答案为4.
15. 如图,在中,D,E,F,分别时AB,BC,AC,的中点,若平移平移,则图中能与它重合的三角形是_____.(写出一个即可)
【正确答案】△DBE(或△FEC).
【分析】根据平移的性质,图形对图中三角形进行分析,得到正确结果.
【详解】△DBE形状和大小没有变化,属于平移得到;△DEF方向发生了变化,没有属于平移得到;△FEC形状和大小没有变化,属于平移得到.所以图中能与它重合的三角形是△DBE(或△FEC).故答案为△DBE(或△FEC).
本题考查平移的基本性质:①平移没有改变图形的形状和大小;②平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
16. 如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于________度
【正确答案】2n
【详解】如图①,过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
如图②,∵∠ABE和∠DCE的平分线交点为E1,
∴∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC.
∵∠ABE1和∠DCE1的平分线交点为E2,
∴∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC;
如图②,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;
…
以此类推,∠En=∠BEC.
∴当∠En=1度时,∠BEC等于2n度.
故2n .
本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
三.解 答 题(共7小题)
17. 已知直线AB∥CD.
(1)如图1,直接写出,和之间的数量关系.
(2)如图2,,分别平分,,那么和有怎样的数量关系?请说明理由.
(3)若点E的位置如图3所示,,仍分别平分,,请直接写出和的数量关系.
【正确答案】(1);
(2),理由见解析;
(3),理由见解析
【分析】(1)过点E作EF∥AB,根据平行线的性质得,,进而即可得到结论;
(2)由角平分线的定义得,,第(1)题的结论,即可求证;
(3)过点作,由平行线性质得,第(1)题的结论与角平分线的定义得,进而即可得到结论.
【小问1详解】
证明:,理由如下:
如图1,过点E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴,,
∴,
即;
【小问2详解】
证明:.理由如下:
∵,分别平分,,
∴,,
∴,
由(1)得,,
又∵,
∴;
【小问3详解】
证明:,理由如下:
如图3,过点作,
∵,,
∴,
∴,,
∴,
由(1)知,,
又∵,分别平分,,
∴,,
∴,
∴.
本题主要考查平行公理的推理,平行线的性质定理与角平分线的定义,添加辅助线,掌握平行线的性质定理是解题的关键.
18. 如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若没有变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若没有存在,说明理由.
【正确答案】(1)与∠AOC相等的角是∠AOC,∠ABC,∠BAM,理由见解析;(2)∠OBC:∠OFC=;(3)没有存在,理由见解析.
【分析】(1)根据两直线平行,同旁内角互补可得求出∠ABC,再根据邻补角的定义求出∠BAM即可得解;
(2)根据两直线平行,内错角相等可得∠OBC=∠AOB,∠OFC=∠AOF,再根据角平分线的定义可得∠AOF=2∠AOB,从而得到比值没有变;
(3)设∠OBA=x,表示出∠OEC,然后利用三角形的内角和定理表示出∠AOB、∠COE,再根据角平分线的定义根据∠AOB+∠COE=∠AOC列出方程求解即可.
【详解】解:(1)∵OM∥CN,
∴∠AOC=180°-∠C=180°-108°=72°,
∠ABC=180°-∠OAB=180°-108°=72°,
又∵∠BAM=∠180°-∠OAB=180°-108°=72°,
∴与∠AOC相等的角是∠ABC,∠BAM;
(2)∵OM∥CN,
∴∠OBC=∠AOB,∠OFC=∠AOF,
∵OB平分∠AOF,
∴∠AOF=2∠AOB,
∴∠OFC=2∠OBC,
∴∠OBC:∠OFC=;
(3)设∠OBA=x,则∠OEC=2x,
在△AOB中,∠AOB=180°-∠OAB-∠ABO=180°-x-108°=72°-x,
在△OCE中,∠COE=180°-∠C-∠OEC=180°-108°-2x=72°-2x,
∵OB平分∠AOF,OE平分∠COF,
∴∠COE+∠AOB=∠COF+∠AOF=∠AOC=×72°=36°,
∴72°-x+72°-2x=36°,
解得x=36°,
即∠OBA=36°,
此时,∠OEC=2×36°=72°,
∠COE=72°-2×36°=0°,
点C、E重合,
所以,没有存在.
考点:平行线的判定与性质.
19. 计算:(﹣)2﹣ ﹣+82.
【正确答案】64
【详解】试题分析:
按实数的相关运算法则计算即可.
试题解析:
原式=2﹣(﹣4)﹣6+64
=2+4﹣6+64
=64
20. 已知m是的整数部分,n是的小数部分,求的值.
【正确答案】
【详解】解:∵3<<4,
∴m=3,n=﹣3,
∴
=
=
= .
21. 阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限没有循环小数,因此 的小数部分我们没有可能全部写出来,于是小明用-1来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<<3,∴ 的整数部分为2,小数部分为 ﹣2.
请解答:
(1)的整数部分是________,小数部分是________.
(2)如果的小数部分为a,的整数部分为b,求a+b- 的值;
(3)已知:x是3+ 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
【正确答案】(1)3;﹣3;(2)4;(3)﹣7.
【详解】试题分析:(1)求出的范围是3<<4,根据题目中所给的方法即可求出答案;
(2)求出的范围是2<<3,求出的范围是6<<7,根据题目中所给的方法求得a、b的值,再代入求值即可;(3)求出的范围,推出3+的范围,题目中所给的方法求出x、y的值,代入即可.
试题解析:
(1)的整数部分是3,小数部分是﹣3;
故答案为3;﹣3;
(2)∵4<5<9,
∴2<<3,即a=﹣2,
∵36<37<49,
∴6<<7,即b=6,
则a+b﹣=4;
(3)根据题意得:x=5,y=3+﹣5=﹣2,
∴x﹣y=7﹣,其相反数是﹣7.
点睛:本题考查了估计无理数的大小,代数式求值等知识点的应用,解题的关键是关键根据题意求出无理数的取值范围.
22. 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)在图中画出△A′B′C′,并写出点A′、B′、C′的坐标;
(2)在y轴上求点P,使得△BCP与△ABC面积相等.
【正确答案】(1)A′(0,4)B′(﹣1,1),C′(3,1);(2)P(0,1)或(0,﹣5)
【分析】(1)根据图形平移的性质画出,并写出点的坐标即可
(2)根据△ABC和△BCP同底,画图进而可得出结论.
【详解】解:(1)如图,即为所求.
(2)△ABC的面积是:,△ABC和△BCP同底,
在y轴上存在一点P,使得△BCP与△ABC面积相等,如图,
点P的坐标为(0,1)或(0,-5).
本题考查图形的平移,以及三角形的面积公式,解题的关键是掌握图形的平移是找到平移之后的对应点,顺次连接即可.
23. 如图,已知AM//BN,,点是射线上一动点(与点没有重合),、分别平分和,分别交射线于、.
(1)求的度数;
(2)在点P的运动过程中,∠APB与∠ADB之间的数量关系是否随之发生变化?若没有变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数是 ,并说明理由.
【正确答案】(1)∠CBD=60°;(2)没有变化,∠APB=2∠ADB,证明见详解;(3)30°
【分析】(1)根据∠A=60°,则∠ABN=120°,由BC、BD分别平分∠ABP和∠PBN,即可得出的度数;
(2)根据平行线性质得出∠APB=∠PBN,∠ADB=∠DBN,再根据BD平分∠PBN,即可得到∠PBN=2∠DBN进而得出∠APB=2∠ADB;
(3)根据∠ACB=∠CBN,∠ACB=∠ABD,得出∠CBN=∠ABD,进而得到∠ABC=∠DBN,根据∠CBD=60°,∠ABN=120°,可求得∠ABC的度数.
【详解】解:(1)∵AM//BN,,
∴∠ABN=120°,
∴∠ABP+∠P=120°
∵、分别平分和,
∴,,
∴;
(2)没有变化,∠APB=2∠ADB,
证明:∵AM∥BN,
∴∠APB=∠PBN,
∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AD∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠DBN,
由(1)可得,∠CBD=60°,∠ABN=120°,
∴∠ABC=(120°60°)=30°.
故30°.
本题主要考查了平行线的性质,角平分线的性质的运用,解题的关键是掌握:两直线平行,内错角相等.
2022-2023学年贵州省遵义市七年级下册数学第一次月考模拟卷(B卷)
一.选一选:(每小题3分,共36分)
1. 下列图形中与互为对顶角的是( )
A. B. C. D.
2. 的平方根是( )
A. ± B. C. - D. ±4
3. 在图示的四个汽车标志图案中,能用平移交换来分析其形成过程的图案是( )
A. B. C. D.
4. 在同一平面内,两条直线的位置关系可能是( )
A. 相交或平行 B. 相交或垂直 C. 平行或垂直 D. 没有能确定
5. 如图,下列说法中没有正确的是( )
A. 和是同旁内角 B. 和是内错角
C. 和是同位角 D. 和是对顶角
6. 下列说法没有正确的是( )
A. 8的立方根是2 B. -8的立方根是-2
C. 0的立方根是0 D. 125的立方根是±5
7. 如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )
A. 40° B. 50° C. 60° D. 140°
8. 下列图形中,线段AD的长表示点A到直线BC距离的是( )
A. B. C. D.
9. 若A、B、C是直线l上三点,P是直线l外一点,且PA=5cm,PB=4cm,PC=3cm,
则点P到直线l的距离 ( )
A 等于3 cm B. 大于3 cm而小于4 cm ; C. 没有大于3 cm D. 小于3 cm
10. 如图,下列能判定AB∥EF的条件有( )
①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A. 1个 B. 2个 C. 3个 D. 4个
11. 估计的值在( )
A. 4和5之间 B. 5和6之间 C. 6和7之间 D. 7和8之间
12. 如图,若两条平行线EF,MN与直线AB,CD相交,则图中共有同旁内角的对数为( )
A. 16 B. 12 C. 8 D. 4
二、填 空 题(本大题共6小题,共24分)
13. 如图,已知∠1=∠2,则图中互相平行的线段是___________;
理由:__________________________.
14. 实数的整数部分是_______.
15. 若x,y为实数,且|x+2|+=0,则的值为________.
16. 如图,已知AC⊥BC,CD⊥AB于点D,AC=5cm,BC=12cm,AB=13cm,那么点B到AC的距离是____________cm.
17. 小红做了棱长为5cm的一个正方体盒子,小明说:“我做的盒子的体积比你的大218 cm3”则小明的盒子的棱长为_____cm
18. 观察数表:
根据数表排列的规律,第10行从左向右数第8个数是____.
三、解 答 题(本大题共90分)
19. 计算(1)(﹣3)2+|-1|﹣ (2)|-2|+-(-1)2017;
20. 求x的值(1)27﹣(x+4)3=0; (2)2(x﹣1)2=.
21. 填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
22. 一个正数x的平方根是3a-4和1-6a,求a及x的值.
23. 已知|2a+b|与互为相反数,求2a-3b的平方根.
24. 如图,已知点A,D,B在同一直线上,∠1=∠2,∠3=∠E,若∠DAE=100°,∠E=30°,求∠B的度数.
25. 如图,BD⊥AC于点D,EF⊥AC于点F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC
26. 某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
27. 已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D没有重合,如图2和图3),上述(1)中的结论是否还成立?若没有成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,没有必写理由.
2022-2023学年贵州省遵义市七年级下册数学第一次月考模拟卷(B卷)
一.选一选:(每小题3分,共36分)
1. 下列图形中与互为对顶角的是( )
A. B. C. D.
【1题答案】
【正确答案】B
【详解】解:A.∠1与∠2没有是对顶角,故此选项错误;
B.∠1与∠2是对顶角,故此选项正确;
C.∠1与∠2没有是对顶角,故此选项错误;
D.∠1与∠2没有是对顶角,故此选项错误.
故选B.
2. 的平方根是( )
A. ± B. C. - D. ±4
【2题答案】
【正确答案】A
【详解】∵,
∴的平方根是.
故选A.
3. 在图示的四个汽车标志图案中,能用平移交换来分析其形成过程的图案是( )
A. B. C. D.
【3题答案】
【正确答案】C
【详解】解:根据平移的概念,观察图形可知图案C通过平移后可以得到.故选C.
点睛:本题主要考查了图形的平移,在平面内,把一个图形整体沿某一的方向移动,学生混淆图形的平移与旋转或翻转,而误选.
4. 在同一平面内,两条直线的位置关系可能是( )
A. 相交或平行 B. 相交或垂直 C. 平行或垂直 D. 没有能确定
【4题答案】
【正确答案】A
【分析】根据同一平面内,两条直线的位置关系即可得到结论.
【详解】解:在同一平面内,两条直线只有两种位置关系:相交或平行,
故选:A.
本题考查平面内两条直线的位置关系,注意垂直是相交的情况,包括在相交里.
5. 如图,下列说法中没有正确的是( )
A. 和是同旁内角 B. 和是内错角
C. 和是同位角 D. 和是对顶角
【5题答案】
【正确答案】C
【详解】解:A. ∠1和∠3是同旁内角,正确,没有合题意;
B. ∠2和∠3是内错角,正确,没有合题意;
C. ∠2和∠4是同位角,错误,符合题意;
D. ∠3和∠5是对顶角,正确,没有合题意;
故选:C.
6. 下列说法没有正确的是( )
A. 8的立方根是2 B. -8的立方根是-2
C. 0的立方根是0 D. 125的立方根是±5
【6题答案】
【正确答案】D
【详解】解:A. 8的立方根是2,说确,没有符合题意;
B. -8的立方根是-2,说确,没有符合题意;
C. 0的立方根是0,说确,没有符合题意;
D. 125的立方根是5,说法没有正确,符合题意;
故选D
本题考查了求一个数的立方根,正数的立方根是正数,0的立方根是0,负数的立方根是负数.
7. 如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是( )
A. 40° B. 50° C. 60° D. 140°
【7题答案】
【正确答案】A
【详解】试题分析:根据直角三角形两锐角互余求出∠3,再根据两直线平行,同位角相等解答.
解:∵DB⊥BC,∠2=50°,
∴∠3=90°﹣∠2=90°﹣50°=40°,
∵AB∥CD,
∴∠1=∠3=40°.
故选A.
8. 下列图形中,线段AD的长表示点A到直线BC距离的是( )
A. B. C. D.
【8题答案】
【正确答案】D
【分析】根据点到直线的距离定义逐项判断即可.
【详解】解:A中的AD没有垂直BC,所以线段AD的长没有是点A到直线BC距离,故此选项错误;
B中的AD没有垂直BC,所以线段AD的长没有是点A到直线BC距离,故此选项错误;
C中的AD没有垂直BC,所以线段AD的长没有是点A到直线BC距离,故此选项错误;
D中的AD⊥BC,所以线段AD的长是点A到直线BC距离,故此选项正确,
故选:D.
本题考查点到直线的距离定义,熟知点到直线的距离定义是解答的关键.
9. 若A、B、C是直线l上的三点,P是直线l外一点,且PA=5cm,PB=4cm,PC=3cm,
则点P到直线l的距离 ( )
A. 等于3 cm B. 大于3 cm而小于4 cm ; C. 没有大于3 cm D. 小于3 cm
【9题答案】
【正确答案】C
【分析】根据直线外一点到直线上各点所有线中,垂线段最短进行解答.
【详解】解:∵直线外一点与直线上各点连接的所有线段中,垂线段最短,
∴点P到直线l的距离≤PC,即点P到直线l的距离没有大于3cm.
故选:C.
本题考查的是点到直线的距离,熟知“垂线段最短”是解答此题的关键.
10. 如图,下列能判定AB∥EF条件有( )
①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A. 1个 B. 2个 C. 3个 D. 4个
【10题答案】
【正确答案】C
【分析】根据平行线的判定定理分别进行判断即可.
【详解】解:当∠B+∠BFE=180°,AB∥EF;故①满足题意;
当∠1=∠2时,DE∥BC;故②没有满足题意;
当∠3=∠4时,AB∥EF;故③满足题意;
当∠B=∠5时,AB∥EF.故④满足题意;
故选C.
本题考查平行线的判定.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
11. 估计的值在( )
A. 4和5之间 B. 5和6之间 C. 6和7之间 D. 7和8之间
【11题答案】
【正确答案】C
【详解】解:由36<38<49,即可得6<<7,
故选:C.
12. 如图,若两条平行线EF,MN与直线AB,CD相交,则图中共有同旁内角的对数为( )
A. 16 B. 12 C. 8 D. 4
【12题答案】
【正确答案】A
【详解】解:以CD为截线,
①若以EF、MN为被截直线,有2对同旁内角,
②若以AB、EF为被截直线,有2对同旁内角,
③若以AB、MN为被截直线,有2对同旁内角;
综上,以CD为截线共有6对同旁内角.
同理:以AB为截线又有6对同旁内角.
以EF为截线,以AB、CD为被截直线,有2对同旁内角,
以MN为截线,以AB、CD为被截直线,有2对同旁内角,
综上,共有16对同旁内角.故选A.
点睛:解答此题的关键在掌握同旁内角的概念,注意要对截线的情况进行讨论.
二、填 空 题(本大题共6小题,共24分)
13. 如图,已知∠1=∠2,则图中互相平行的线段是___________;
理由是:__________________________.
【13题答案】
【正确答案】 ①. AD∥BC ②. 内错角相等,两直线平行
【详解】解:∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行).故答案为AD∥BC, 内错角相等,两直线平行.
14. 实数的整数部分是_______.
【14题答案】
【正确答案】3
【详解】解:∵3<<4,∴a=3.故答案为3.
15. 若x,y为实数,且|x+2|+=0,则的值为________.
【15题答案】
【正确答案】-1
【详解】解:由题意得:x+2=0,y-2=0,
解得:x=﹣2,y=2,
所以==-1.
故答案为-1.
16. 如图,已知AC⊥BC,CD⊥AB于点D,AC=5cm,BC=12cm,AB=13cm,那么点B到AC的距离是____________cm.
【16题答案】
【正确答案】12
【详解】解:∵AC⊥BC,BC=12cm,∴点B到AC的距离为12cm.故答案为12.
点睛:本题主要考查点到直线的距离,关键在于推出点B到AC的距离为BC的长度.
17. 小红做了棱长为5cm的一个正方体盒子,小明说:“我做的盒子的体积比你的大218 cm3”则小明的盒子的棱长为_____cm
【17题答案】
【正确答案】7
【分析】首先利用正方体的体积公式求出体积,再利用立方根的定义求值即可.
【详解】小红做的正方体的盒子的体积是53=125cm3.
则小明的盒子的体积是125+218=343cm3.
设盒子的棱长为xcm,则
x3=343
∵73=343
∴x=7
故盒子的棱长为7cm.
故7.
本题考查了正方体的体积等于边长的三次方和立方根的运算.解答本题的关键是要掌握好正方体的体积公式.
18. 观察数表:
根据数表排列的规律,第10行从左向右数第8个数是____.
【18题答案】
【正确答案】
【详解】观察、分析表格中的数据可知,第n行第n个数是,从它往左,被开方数依次减1,从它往右,被开方数依次加1,
∴第10行第10个数是,
∴第10行第8个数是.
故答案为.
点睛:本题的解题要点是:通过观察、分析所给数据组得到结论:行个数是,第二行第二个数是,第三行的第三个数是,……,由此得到第n行的第n个数是,这样再同一行中,相邻的两个数的被开方数右边的比左边的大1即可解出本题了.
三、解 答 题(本大题共90分)
19. 计算(1)(﹣3)2+|-1|﹣ (2)|-2|+-(-1)2017;
【19题答案】
【正确答案】(1)7;(2)1
【详解】试题分析:(1)根据乘方、值、立方根的意义计算即可;
(2)根据值、立方根、乘方的意义计算即可.
试题解析:解:(1)原式=9 +1-3=7 ;
(2)原式=2-2+1=1.
20. 求x的值(1)27﹣(x+4)3=0; (2)2(x﹣1)2=.
【20题答案】
【正确答案】(1)x=-1;(2) x=3或x=﹣1
【详解】试题分析:(1)先求得(x+4)3的值,然后利用立方根的定义列方程求解即可;
(2)先求得(x﹣1)2的值,然后利用平方根的定义列方程求解即可.
试题解析:解:(1)∵27﹣(x+4)3=0,∴(x+4)3=27,∴x+4=3,解得:x=﹣1.
(2)∵2(x﹣1)2=,∴(x﹣1)2=4,∴x﹣1=±2,解得:x=3或x=﹣1.
点睛:本题主要考查的是平方根、立方根的定义,依据平方根和立方根的定义列出关于x的方程是解题的关键.
21. 填写推理理由:
如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
证明:∵CD∥EF,
∴∠DCB=∠2( ),
∵∠1=∠2,
∴∠DCB=∠1( ).
∴GD∥CB( ),
∴∠3=∠ACB( ).
【21题答案】
【正确答案】两直线平行,同位角相等;等量代换;内错角相等,两直线平行;两直线平行,同位角相等
【分析】根据平行线的性质得出∠2=∠DCB,求出∠1=∠DCB,根据平行线的判定得出GD∥CB即可.
【详解】解:∵CD∥EF,
∴∠DCB=∠2(两直线平行,同位角相等)
∵∠1=∠2,
∴∠DCB=∠1.(等量代换)
∴GD∥CB(内错角相等,两直线平行).
∴∠3=∠ACB(两直线平行,同位角相等).
22. 一个正数x的平方根是3a-4和1-6a,求a及x的值.
【22题答案】
【正确答案】a的值是-1,x的值是49
【详解】试题分析:根据一个正数有两个平方根,且它们互为相反数,可直接根据互为相反数的两数和为0,列式求解出a的值,再根据乘方代入求出x即可.
试题解析:由题意得3a-4+1-6a=0,
解得a=-1.
∴3a-4=-7.
∴x=(-7)2=49.
答:a的值是-1,x的值是49.
23. 已知|2a+b|与互为相反数,求2a-3b的平方根.
【23题答案】
【正确答案】±4
【详解】试题分析:依据非负数的性质可求得a、b的值,然后再求得2a﹣3b的值,依据平方根的定义求解即可.
试题解析:解:由题意得:2a+b=0,3b+12=0,解得:b=﹣4,a=2.
∵2a﹣3b=2×2﹣3×(﹣4)=16,∴2a﹣3b的平方根为±4.
24. 如图,已知点A,D,B在同一直线上,∠1=∠2,∠3=∠E,若∠DAE=100°,∠E=30°,求∠B度数.
【24题答案】
【正确答案】50°.
【详解】分析:根据平行线的判定定理得到AE∥DC,由平行线的性质得到∠CDE=∠E,推出DE∥BC,得到∠B=∠ADE,于是得到结论.
本题解析:
∵∠1=∠2,∴AE∥DC,∴∠CDE=∠E,
∵∠3=∠E,∴∠CDE=∠3,∴DE∥BC,∴ ∠B=∠ADE
∵∠ADE=180°﹣∠DAE﹣∠E=50°,
∴∠B=50°.
25. 如图,BD⊥AC于点D,EF⊥AC于点F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
【25题答案】
【正确答案】(1)125°;(2)证明见解析
【分析】(1)由BD⊥AC,EF⊥AC,得到BD∥EF,根据平行线的性质得到∠EFG=∠1=35°,再根据角的和差关系可求∠GFC的度数;
(2)根据平行线性质得到∠2=∠CBD,等量代换得到∠1=∠CBD,根据平行线的判定定理得到GF∥BC,证得MD∥GF,根据平行线的性质即可得到结论.
【详解】解:(1)∵BD⊥AC,EF⊥AC,
∴BD∥EF,
∴∠EFG=∠1=35°,
∴∠GFC=90°+35°=125°;
(2)∵BD∥EF,
∴∠2=∠CBD,
∴∠1=∠CBD,
∴GF∥BC.
∵∠AMD=∠AGF,
∴MD∥GF,
∴DM∥BC.
本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质是解题的关键.
26. 某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
【26题答案】
【正确答案】安排10人生产螺钉,12人生产螺母.
【详解】试题分析:设分配x名工人生产螺母,则(22﹣x)人生产螺钉,由一个螺钉配两个螺母可知螺母的个数是螺钉个数的2倍从而得出等量关系,就可以列出方程求出即可.
试题解析:解:设分配x名工人生产螺母,则(22﹣x)人生产螺钉,由题意得:
2000x=2×1200(22﹣x),解得:x=12,则22﹣x=10.
答:应安排10人生产螺钉,12名工人生产螺母.
点睛:此题主要考查了一元方程的应用,列方程解应用题的步骤及掌握解应用题的关键是建立等量关系.
27. 已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D没有重合,如图2和图3),上述(1)中的结论是否还成立?若没有成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,没有必写理由.
【27题答案】
【正确答案】(1)∠APB=∠PAC+∠PBD;(2)没有成立
【分析】(1)当P点在C、D之间运动时,首先过点P作PE∥l1,由l1∥l2,可得PE∥l2∥l1,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD.
(2)当点P在C、D两点的外侧运动时,由直线l1∥l2,根据两直线平行,同位角相等与三角形外角的性质,即可求得:∠PAC=∠PBD+∠APB或∠PBD=∠PAC+∠APB.
【详解】(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)没有成立
如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
考查平行线的判定与性质,三角形外角的性质等,三角形的一个外角等于与它没有相邻的两个内角的和.
相关试卷
这是一份2022-2023学年重庆市荣昌区七年级下册数学第一次月考模拟卷(AB卷)含解析,共39页。试卷主要包含了 下列说法没有正确的是,2的算术平方根是0, 下列各组数中互为相反数是, 下列语句错误的是等内容,欢迎下载使用。
这是一份2022-2023学年江苏省无锡市七年级下册数学第一次月考模拟卷(AB卷)含解析,共41页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
这是一份2022-2023学年北京市平谷区七年级下册数学第一次月考模拟卷(AB卷)含解析,共33页。试卷主要包含了选一选,填 空 题,计算,解 答 题等内容,欢迎下载使用。










