2022-2023学年江苏省无锡市七年级下册数学第一次月考模拟卷（AB卷）含解析

这是一份2022-2023学年江苏省无锡市七年级下册数学第一次月考模拟卷（AB卷）含解析，共41页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。
2022-2023学年江苏省无锡市七年级下册数学第一次月考模拟卷（A卷）
一、选一选（共8小题，每小题3分，满分24分）
1. 给出以下命题：①对顶角相等；②在同一平面内， 垂直于同一条直线的两条直线平行；③相等的角是对顶角；④内错角相等．其中假命题有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
2. 点P是直线l外一点，PA垂直于直线l，垂足为A ,且PA=4 cm，则点P到直线l的距离（ ）
A. 小于4 cm B. 等于4 cm C. 大于4 cm D. 没有确定
3. 如图所示的四个图形中，∠1和∠2是同位角的是（ ）

A. ②③ B. ①②③ C. ①②④ D. ①④
4. 如图，点E在的延长线上，下列条件没有能判断的是（ ）

A. B. C. D.
5. 如图，若∠1=70°，∠2=110°，∠3=70°，则有（　 　）．

A. a∥b B. c∥d C. a⊥d D. 任两条都无法判定否平行
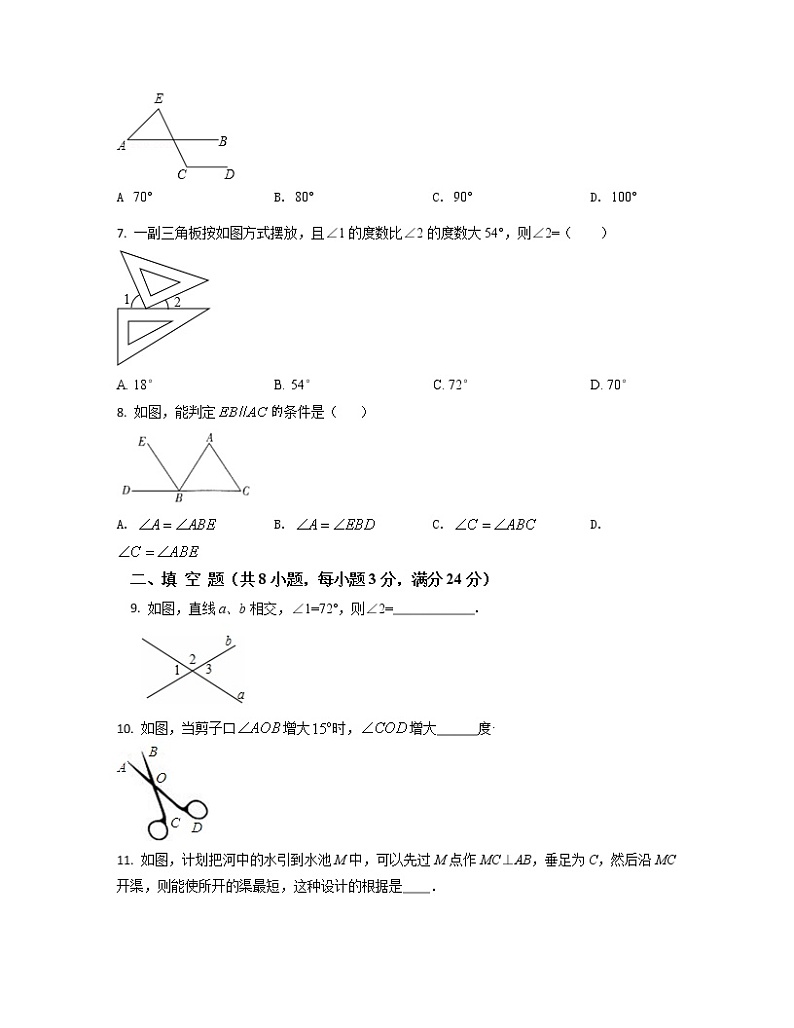
6. 如图，已知直线AB∥CD，∠C=125°，∠A=45°，那么∠E大小为（ ）

A 70° B. 80° C. 90° D. 100°
7. 一副三角板按如图方式摆放，且∠1的度数比∠2的度数大54°，则∠2=（　　）

A. 18° B. 54° C. 72° D. 70°
8. 如图，能判定条件是（ ）

A. B. C. D.
二、填 空 题（共8小题，每小题3分，满分24分）
9. 如图，直线a、b相交，∠1=72°，则∠2=____________．

10. 如图，当剪子口增大时，增大______度

11. 如图，计划把河中的水引到水池M中，可以先过M点作MC⊥AB，垂足为C，然后沿MC开渠，则能使所开的渠最短，这种设计的根据是____．

12. 将“对顶角相等”改写为“如果．．．那么．．．”的形式，可写为__________．
13. 如图，D是AB上一点，CE∥BD，CB∥ED，EA⊥BA于点A，若∠ABC=38°，则∠AED= ____．

14. 如图，，直线EF分别交AB、CD于E、F，EG平分∠BEF，若∠1=72°,则∠2=____．

15. 如图，直线a∥b，则∠ACB=______

16. 如图，一个宽度相等的纸条按如图所示方法折叠一下，则________度．


三、解 答 题（共6小题，满分46分）
17. 如图，直线CD与直线AB相交于C，根据下列语句画图、解答．
（1）过点P作PQCD，交AB于点Q；
（2）过点P作PR⊥CD，垂足为R；
（3）若∠DCB=120°，猜想∠PQC是多少度？并说明理由


18. 如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1=25°,求∠2度数？

19. 如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.

20. 如图，AB∥CE，CE平分∠DCB，求证∠A=∠B

21. 如图，已知∠ACD＝70°，∠ACB＝60°，∠ABC＝50°．试说明：AB∥CD．

22. 根据下列证明过程填空：
如图，已知BD⊥AC，EF⊥AC，D、F分别为垂足，且∠1=∠4，求证：∠ADG=∠C

证明：∵BD⊥AC，EF⊥AC
∴∠2=∠3=90°（ ）
∴BD∥EF ( )
∴∠4=_____( )
∵∠1=∠4
∴∠1=_____( )
∴DG∥BC( )
∴∠ADG=∠C( )
23. 如图，直线EF分别与直线AB，CD相交于点P和点Q，且AB//CD，PG平分∠APQ，QH平分∠DQP，求证：PG//QH.







2022-2023学年江苏省无锡市七年级下册数学第一次月考模拟卷（A卷）
一、选一选（共8小题，每小题3分，满分24分）
1. 给出以下命题：①对顶角相等；②在同一平面内， 垂直于同一条直线两条直线平行；③相等的角是对顶角；④内错角相等．其中假命题有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
【正确答案】B

【分析】根据对顶角的性质、平行线的判定和性质进行判断即可．
【详解】解：①对顶角相等，是真命题；
②在同一平面内，垂直于同一条直线的两条直线平行，是真命题；
③相等的角没有一定是对顶角，原命题是假命题；
④两直线平行，内错角相等，原命题是假命题．
故选：B．
考查了命题与定理的知识，解题的关键是了解对顶角的性质、平行线的判定和性质，难度较小．
2. 点P是直线l外一点，PA垂直于直线l，垂足为A ,且PA=4 cm，则点P到直线l的距离（ ）
A. 小于4 cm B. 等于4 cm C. 大于4 cm D. 没有确定
【正确答案】B

【详解】根据点到直线的距离为点到直线的垂线段长（垂线段最短），
所以，点P到直线l的距离等于4 cm，
故选B．
3. 如图所示的四个图形中，∠1和∠2是同位角的是（ ）

A. ②③ B. ①②③ C. ①②④ D. ①④
【正确答案】C

【分析】根据同位角的定义逐一判断即得答案．
【详解】解：图①中的∠1与∠2是同位角，图②中的∠1与∠2是同位角，图③中的∠1与∠2没有是同位角，图④中的∠1与∠2是同位角，
所以在如图所示的四个图形中，图①②④中的∠1和∠2是同位角．
故选：C．
本题考查了同位角的定义，属于基础概念题型，熟知概念是关键．
4. 如图，点E在的延长线上，下列条件没有能判断的是（ ）

A. B. C. D.
【正确答案】D

【分析】直接利用平行线的判定方法分别判断得出答案．
【详解】解：A、当∠5=∠B时，AB∥CD，没有合题意；
B、当∠1=∠2时，AB∥CD，没有合题意；
C、当∠B+∠BCD=180°时，AB∥CD，没有合题意；
D、当∠3=∠4时，AD∥CB，符合题意；
故选：D．
此题主要考查了平行线的判定，正确掌握平行线的判定方法是解题关键．
5. 如图，若∠1=70°，∠2=110°，∠3=70°，则有（　 　）．

A. a∥b B. c∥d C. a⊥d D. 任两条都无法判定是否平行
【正确答案】A

【详解】解：∵∠4=∠1=70°，∠2=110°，
∴∠4+∠2=180°；
∴a∥b．
∵∠2≠∠3，
∴c与d没有平行．
故选A．

6. 如图，已知直线AB∥CD，∠C=125°，∠A=45°，那么∠E的大小为（ ）

A. 70° B. 80° C. 90° D. 100°
【正确答案】B

【分析】根据两直线平行，同位角相等，及邻补角的定义求得∠EFA=55°，再利用三角形内角和定理即可求得∠E的度数．
【详解】解：如图所示，

∵AB∥CD，∠C=125°，
∴∠C=∠EFB=125°，
∴∠EFA=180-125=55°，
∵∠A=45°，
∴∠E=180°-∠A-∠EFA=180°-45°-55°=80°．
故选：B．
本题应用的知识点为：根据两直线平行，同位角相等，邻补角的定义，三角形内角和定理．
7. 一副三角板按如图方式摆放，且∠1的度数比∠2的度数大54°，则∠2=（　　）

A. 18° B. 54° C. 72° D. 70°
【正确答案】A

【分析】根据题意图形列出方程组，解方程组即可．
【详解】解：由题意得，，解得∠1=72°，∠2=18°，
故选A．
本题考查的是余角和补角的概念和性质，两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补．
8. 如图，能判定的条件是（ ）

A. B. C. D.
【正确答案】A

【分析】根据平行线的判定定理即可依次判断．
【详解】A.，根据同位角相等，两直线平行可以判定；
B.，没有判定；
C.，没有判定；
D，没有判定；
故选A．
此题主要考查平行线的判定定理，解题的关键是熟知同位角相等，两直线平行．
二、填 空 题（共8小题，每小题3分，满分24分）
9. 如图，直线a、b相交，∠1=72°，则∠2=____________．

【正确答案】108°

详解】试题解析：∵直线a∥b，
∴∠2=∠3，
∵∠1=72°，
∴∠3=108°，
∴∠2=108°，

故答案为108°.
10. 如图，当剪子口增大时，增大______度

【正确答案】15

【详解】分析：根据对顶角的定义和性质求解．
详解：因为∠AOB与∠COD是对顶角，∠AOB与∠COD始终相等，所以随∠AOB变化，∠COD也发生同样变化．
故当剪子口∠AOB增大15°时，∠COD也增大15°．
点睛：互为对顶角的两个角相等，如果一个角发生变化，则另一个角也做相同的变化．
11. 如图，计划把河中的水引到水池M中，可以先过M点作MC⊥AB，垂足为C，然后沿MC开渠，则能使所开的渠最短，这种设计的根据是____．

【正确答案】垂线段最短

【分析】根据垂线段的性质：垂线段最短，进行判断即可．
【详解】解：∵从直线外一点到这条直线上各点所连线段中，垂线段最短，
∴过M点作MC⊥AB于点C，则MC最短，
这样做的依据是垂线段最短．
故垂线段最短．
本题考查了垂线段的性质，从直线外一点到这条直线上各点所连线段中，垂线段最短，掌握基本性质是解题关键．
12. 将“对顶角相等”改写为“如果．．．那么．．．”的形式，可写为__________．
【正确答案】如果两个角互对顶角，那么这两个角相等

【分析】根据命题的形式解答即可．
【详解】将“对顶角相等”改写为“如果．．．那么．．．”的形式，可写为如果两个角互为对顶角，那么这两个角相等，
故如果两个角互为对顶角，那么这两个角相等．
此题考查命题的形式，可写成用关联词“如果．．．那么．．．”连接的形式，准确确定命题中的题设和结论是解题的关键．
13. 如图，D是AB上一点，CE∥BD，CB∥ED，EA⊥BA于点A，若∠ABC=38°，则∠AED= ____．

【正确答案】52°

【详解】∵ EA⊥BA，
∴ ∠EAD=90°，
∵ CB∥ED，∠ABC=38°，
∴ ∠EDA=∠ABC=38°，
∴ ∠AED=180°-∠EAD-∠EDA=52°，
故答案为52°．
本题考查了平行线的性质、垂直的定义等，准确识图是解题的关键.
14. 如图，，直线EF分别交AB、CD于E、F，EG平分∠BEF，若∠1=72°,则∠2=____．

【正确答案】54°

【分析】两直线平行，同旁内角互补，可求出∠FEB，再根据角平分线的性质，可得到∠BEG，然后用两直线平行，内错角相等求出∠2．
【详解】解：∵AB∥CD，
∴∠BEF=180°−∠1=180°−72°=108°
∠2=∠BEG，
又∵EG平分∠BEF，
∴∠BEG=∠BEF=×108°=54°
∴∠2=∠BEG=54°
故54°.
15. 如图，直线a∥b，则∠ACB=______

【正确答案】78°##78度

【详解】如图，延长BC与a相交，已知a∥b，根据两直线平行，内错角相等可得∠1=∠50°；再由三角形的外角的性质可得∠ACB=∠1+28°=50°+28°=78°.

故78°.
点睛：本题主要考查平行线的性质和三角形外角性质，较为简单，属于基础题．
16. 如图，一个宽度相等的纸条按如图所示方法折叠一下，则________度．


【正确答案】65

【分析】根据两直线平行内错角相等，以及折叠关系列出方程求解则可．
【详解】解：如图，由题意可知，

由题意知ABCD，
∴∠1+∠2=130°，
由折叠可知，∠1=∠2，
∴2∠1＝130°，
解得∠1＝65°．
故65．
本题考查了平行线的性质和折叠的知识，根据折叠得出∠1=∠2是解题的关键．
三、解 答 题（共6小题，满分46分）
17. 如图，直线CD与直线AB相交于C，根据下列语句画图、解答．
（1）过点P作PQCD，交AB于点Q；
（2）过点P作PR⊥CD，垂足为R；
（3）若∠DCB=120°，猜想∠PQC是多少度？并说明理由


【正确答案】（1）见解析；（2）见解析；（3）∠PQC=60°，理由见解析

【详解】解：如图所示：


（1）画出如图直线PQ
（2）画出如图直线PR
（3）∠PQC=60°
理由是：因为PQCD
所以∠DCB+∠PQC=180°
又因为∠DCB=120°
所以∠PQC=180°－120°=60°
18. 如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1=25°,求∠2的度数？

【正确答案】65°

【详解】试题分析：直接利用邻补角的定义得出∠BOE=65°，再根据对顶角相等，即可得出答案．
试题解析：∵直线AB，CD，EF相交于点O，且AB⊥CD
∴∠BOC=90°，
∵∠1=25°，
∴∠BOE=65°，
∴∠2=∠BOE=65°．
19. 如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.

【正确答案】40°

【分析】根据平行线的性质可得∠ACB=∠AED=80°，∠EDC=∠BCD，然后根据角平分线的定义可得∠BCD=∠ACB=40°，从而求出结论．
【详解】解：∵DE∥BC,∠AED=80°
∴∠ACB=∠AED=80°，∠EDC=∠BCD
∵CD平分∠ACB,
∴∠BCD=∠ACB=40°
∴∠EDC=40°
此题考查的是平行线的性质和角平分线的定义，掌握平行线的性质是解决此题的关键．
20. 如图，AB∥CE，CE平分∠DCB，求证∠A=∠B

【正确答案】见解析

【详解】试题分析：由AB∥CE，根据两直线平行，内错角相等，同位角相等，即可证得∠DCE=∠A，∠BCE=∠B，又由CE平分∠DAC，即可得∠A=∠B．
试题解析：∵AB∥CE，
∴∠DCE=∠A，∠BCE=∠B，
∵CE平分∠DAC，
∴∠DCE=∠BCE，
∴∠A=∠B．
21. 如图，已知∠ACD＝70°，∠ACB＝60°，∠ABC＝50°．试说明：AB∥CD．

【正确答案】证明见解析

【分析】根据同旁内角互补，两直线平行即可判定．
【详解】证明：



∥ ．
22. 根据下列证明过程填空：
如图，已知BD⊥AC，EF⊥AC，D、F分别为垂足，且∠1=∠4，求证：∠ADG=∠C

证明：∵BD⊥AC，EF⊥AC
∴∠2=∠3=90°（ ）
∴BD∥EF ( )
∴∠4=_____( )
∵∠1=∠4
∴∠1=_____( )
∴DG∥BC( )
∴∠ADG=∠C( )
【正确答案】答案见解析

【详解】解：∵BD⊥AC，EF⊥AC（已知），
∴∠2=∠3=90°，
∴BD∥EF（同位角相等，两直线平行），
∴∠4=∠5（两直线平行，同位角相等）；
∵∠1=∠4（已知），
∴∠1=∠5（等量代换），
∴DG∥BC（内错角相等，两直线平行），
∴∠ADG=∠C（两直线平行，同位角相等）．
本题考查平行线的性质与判定，解决问题要熟悉平行线的性质和判定，能正确运用语言叙述理由，还要注意平行线的性质和判定的综合运用．
23. 如图，直线EF分别与直线AB，CD相交于点P和点Q，且AB//CD，PG平分∠APQ，QH平分∠DQP，求证：PG//QH.

【正确答案】见解析

【详解】先根据角平分线的性质可得∠1=∠GPQ=∠APQ，∠2=∠PQH=∠EQD，根据条件AB//CD，可得∠APQ=∠PQD，∠GPQ=∠PQH，根据内错角相等两直线平行可证明PG∥QH．
试题解析：∵PG平分∠APQ，QH平分∠DQP，
∴∠GPQ=∠1=∠APQ，∠PQH=∠2=∠EQD，
∵AB//CD，
∴∠APQ=∠EQD
∴∠GPQ=∠PQH
∴PG∥QH．


















2022-2023学年江苏省无锡市七年级下册数学第一次月考模拟卷（B卷）
一、选一选（每题3分，共24分）
1. 下列运动中：①荡秋千；②钟摆的摆动；③拉抽屉时的抽屉；④工厂里的输送带上的物品，没有属于平移的有（　　）
A. 4个 B. 3个 C. 2个 D. 1个
2. 如图，点E在的延长线上，下列条件没有能判断的是（ ）

A. B. C. D.
3. 下列图形中，正确画出AC边上的高的是（ ）
A. B.
C. D.
4. 下列运算正确的是（　　）
A. B. C. D.
5. 如果三角形有两个外角的和为270°，则此三角形一定是(　　)
A. 锐角三角形 B. 等边三角形 C. 直角三角形 D. 钝角三角形
6. 若a＝－0.3－2，b＝－3－2，c＝(－)－2，d＝(－)0，则( )
A a＜d＜c＜b B. b＜a＜d＜c C. a＜d＜c＜b D. a＜b＜d＜c
7. 如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=（　　）

A. 90°-α B. 90°+ α C. D. 360°-α
8. 定义：直线a与直线b相交于点O，对于平面内任意一点M，点M到直线a与直线b的距离分别为p、q，则称有序实数对（p，q）是点M的“距离坐标”．根据上述定义，“距离坐标”是（1，2）的点的个数是（ ）
A. 1 B. 2 C. 3 D. 4
二、填 空 题（每题3分，共30分）
9. 计算：_______．
10. 某种感冒的直径是0.000000712米，用科学记数法表示为_____米．
11. 已知一个多边形的每一个内角都等于108°，则这个多边形的边数是_____．
12. 若的结果中没有含关于字母的项，则________．
13. 如果是一个完全平方式，那么的值是__________．
14. 已知xa=3，xb=5,则x3a-2b=______________ .
15. 如果一个角的两边与另一个角的两边分别垂直，那么这两个角的关系是_____．
16. 若，则 __________．

17. 如图，在△中，已知点分别为的中点，若△的面积为，则阴影部分的面积为 _________


18. 规定：logab（a>0，a≠1，b>0）表示a，b之间的一种运算．
现有如下的运算法则：=a，logNM=（n>0，n≠1，N>0，N≠1，M>0）．
例如：log223=3，log25=，则=_________．
三、解 答 题（本大题共10小题，共96分）
19. （1） （2）
（3）（3a+2b）（3a﹣2b）（9a2﹣4b2） （4）用简便方法计算：20152﹣2014×2016
20. 规定一种新运算：＝ad－bc.例如，＝3×6－4×5＝－2，＝4x＋6.按照这种运算规定，当x等于多少时， ＝0.
21. 先化简，再求值：（y+1）（2y﹣3）﹣（y+1）2﹣2（y﹣1）（其中y2﹣5y=20）
22. 如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．
（1）请在图中画出平移后的△A′B′C′；
（2）再在图中画出△A′B′C′高C′D′，
（3）写出图中与线段AC平行的线段______．并求出△ABC的面积．


23. 如图，△BCD中，BC=4，BD=5．
（1）求CD的取值范围；
（2）若AE∥BD，∠A=55°，∠BDE=125°，求∠C的度数．

24. 在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）
如图，已知AB∥CD，BE、CF分别平分∠ABC和∠DCB，求证：BE∥CF．

证明：
∵AB∥CD，（已知）
∴∠ =∠ ．（ ）
∵ ，（已知）
∴∠EBC=∠ABC，（角的平分线定义）
同理，∠FCB=∠BCD．
∴∠EBC=∠FCB．（等式性质）
∴BE∥CF．（ ）
25. 已知，如图，在△ABC，∠BAC=80°，AD⊥BC于D，AE平分∠DAC，∠B=60°，求∠DAE的度数．

26. 如图，CD是△ABC的高，点E、F、G分别在BC、AB、AC上，且EF⊥AB，DG∥BC．
试判断∠1、∠2的数量关系，并说明理由．




27. 问题情境：如图1，ABCD，，，求的度数．
小明的思路是：过P作PEAB，通过平行线性质来求．
（1）按小明的思路，易求得的度数为__________度：（直接写出答案）
（2）问题迁移：如图2，ABCD，点P射线上运动，记，，当点P在B、D两点之间运动时，问与、之间有何数量关系？请说明理由；
（3）在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点没有重合），请直接写出与、之间的数量关系．

28. 若∠C=α，∠EAC+∠FBC=β
（1）如图①，AM是∠EAC的平分线，BN是∠FBC的平分线，若AM∥BN，则α与β有何关系？并说明理由．
（2）如图②，若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P，试探究∠APB与α、β的关系是______．（用α、β表示）
（3）如图③，若α≥β，∠EAC与∠FBC平分线相交于P1，∠EAP1与∠FBP1的平分线交于P2 ；依此类推，则∠P5=______．（用α、β表示）

　　





2022-2023学年江苏省无锡市七年级下册数学第一次月考模拟卷（B卷）
一、选一选（每题3分，共24分）
1. 下列运动中：①荡秋千；②钟摆的摆动；③拉抽屉时的抽屉；④工厂里的输送带上的物品，没有属于平移的有（　　）
A. 4个 B. 3个 C. 2个 D. 1个
【1题答案】
【正确答案】C

【详解】试题解析：①荡秋千，是旋转，没有是平移；
②钟摆的摆动，是旋转，没有是平移；
③拉抽屉时的抽屉，是平移；
④工厂里的输送带上的物品，是平移；
故选C．
点睛：平移是指图形的平行移动，平移时图形中所有点移动的方向一致，并且移动的距离相等．
2. 如图，点E在的延长线上，下列条件没有能判断的是（ ）

A. B. C. D.
【2题答案】
【正确答案】D

【分析】直接利用平行线的判定方法分别判断得出答案．
【详解】解：A、当∠5=∠B时，AB∥CD，没有合题意；
B、当∠1=∠2时，AB∥CD，没有合题意；
C、当∠B+∠BCD=180°时，AB∥CD，没有合题意；
D、当∠3=∠4时，AD∥CB，符合题意；
故选：D．
此题主要考查了平行线的判定，正确掌握平行线的判定方法是解题关键．
3. 下列图形中，正确画出AC边上的高的是（ ）
A. B.
C. D.
【3题答案】
【正确答案】D

【分析】根据高的定义即可求解.
【详解】解：根据锐角三角形和钝角三角形的高线的画法，可得D选项中，BE是△ABC中BC边长的高，
故选：D.
【点晴】此题主要考查高作法，解题的关键是熟知高的定义.
4. 下列运算正确的是（　　）
A. B. C. D.
【4题答案】
【正确答案】C

【详解】A. ，原式计算错误，故本选项错误；
B. ，原式计算错误，故本选项错误；
C. ，计算正确，故本选项正确；
D. ，原式计算错误，故本选项错误．
故选C.
5. 如果三角形有两个外角的和为270°，则此三角形一定是(　　)
A. 锐角三角形 B. 等边三角形 C. 直角三角形 D. 钝角三角形
【5题答案】
【正确答案】C

【分析】三角形的外角和为360°，据此进行解答即可.
【详解】解：由题意可知另一个外角为360°－270°＝90°，则与之相邻的内角为90°.
故选C.
本题考查了三角形的外角和，牢记其外角和为360°是解题关键.
6. 若a＝－0.3－2，b＝－3－2，c＝(－)－2，d＝(－)0，则( )
A. a＜d＜c＜b B. b＜a＜d＜c C. a＜d＜c＜b D. a＜b＜d＜c
【6题答案】
【正确答案】B

【详解】根据有理数的乘方、负整数指数幂、零指数幂的意义化简a、b、c、d的值，然后比较大小．由a=−0.09,b=−19，c=9，d=1，得到：c>d>a>b，
故选B.
7. 如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=（　　）

A. 90°-α B. 90°+ α C. D. 360°-α
【7题答案】
【正确答案】C

【详解】试题分析：∵四边形ABCD中，∠ABC+∠BCD=360°﹣（∠A+∠D）=360°﹣α，
∵PB和PC分别为∠ABC、∠BCD的平分线，
∴∠PBC+∠PCB=（∠ABC+∠BCD）=（360°﹣α）=180°﹣α，
则∠P=180°﹣（∠PBC+∠PCB）=180°﹣（180°﹣α）=α．
故选C．
考点：1.多边形内角与外角2.三角形内角和定理．
8. 定义：直线a与直线b相交于点O，对于平面内任意一点M，点M到直线a与直线b的距离分别为p、q，则称有序实数对（p，q）是点M的“距离坐标”．根据上述定义，“距离坐标”是（1，2）的点的个数是（ ）
A. 1 B. 2 C. 3 D. 4
【8题答案】
【正确答案】D

【分析】画出两条相交直线，到a的距离为1的直线有2条，到b的距离为2的直线有2条，看所画的这些直线的交点有几个即为所求的点的个数．
【详解】解：如图所示，所求的点有4个，

故选D．
综合考查点的坐标的相关知识；得到点直线的距离为定值的直线有2条是解决本题的突破点．
二、填 空 题（每题3分，共30分）
9. 计算：_______．
【9题答案】
【正确答案】

【详解】试题解析：4a4b2.
故答案为4a4b2.
10. 某种感冒的直径是0.000000712米，用科学记数法表示为_____米．
【10题答案】
【正确答案】．

【详解】试题解析：0.000000712=7.12×10-7．
考点：科学记数法—表示较小的数．
11. 已知一个多边形的每一个内角都等于108°，则这个多边形的边数是_____．
【11题答案】
【正确答案】5

【详解】解：∵多边形的每一个内角都等于108°
∴每一个外角72°
∵多边形的外角和为360°
∴这个多边形的边数是：360÷72=5
故5
12. 若的结果中没有含关于字母的项，则________．
【12题答案】
【正确答案】﹣2

【分析】原式先根据多项式的乘法法则计算，由结果中没有含关于字母的项可得关于a的一元方程，解方程即得结果．
【详解】解：，
由结果中没有含关于字母的项，可得：，解得：．
故﹣2．
本题考查了多项式乘法，属于基本题型，正确理解题意、熟练掌握多项式乘以多项式的运算法则是解题关键．
13. 如果是一个完全平方式，那么的值是__________．
【13题答案】
【正确答案】或

【分析】利用完全平方公式的结构特征判断即可求出m的值．
【详解】解：∵是一个完全平方式，
∴，
∴或．
故或．
此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．
14. 已知xa=3，xb=5,则x3a-2b=______________ .
【14题答案】
【正确答案】

【详解】分析：根据同底数幂的除法，即可解答．
详解： x3a﹣2b=x3a÷x2b=（xa）3÷（xb）2=33÷52=27÷25=．
故答案为．
点睛：本题考查了同底数幂的除法，解决本题的关键是熟记同底数幂的除法法则．
15. 如果一个角的两边与另一个角的两边分别垂直，那么这两个角的关系是_____．
【15题答案】
【正确答案】相等或互补．

【详解】试题分析：此题可以通过两个图形得出这两个角的关系相等或互补．
解：如图：
图1中，根据垂直的量相等的角都等于90°，对顶角相等，所以∠1=∠2，
图2中，同样根据垂直的量相等的角都等于90°，根据四边形的内角和等于360°，所以∠1+∠2=360°﹣90°﹣90°=180°．
所以如果一个角的两边与另一个角的两边分别垂直，那么这两个角的关系是相等或互补，
故答案为相等或互补．


考点：垂线．
16. 若，则 __________．

【16题答案】
【正确答案】

【详解】试题解析：（m-n）2=（m+n）2-4mn，
当m+n=3，mn=2，原式=32-4×2=1．
∴m-n=±1
故答案为±1．
17. 如图，在△中，已知点分别为的中点，若△的面积为，则阴影部分的面积为 _________


【17题答案】
【正确答案】1

【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答．
【详解】解：∵点E是AD的中点，
∴S△ABE＝S△ABD，S△ACE＝S△ADC，
∴S△ABE＋S△ACE＝S△ABC＝×4＝2cm2，
∴S△BCE＝S△ABC＝×4＝2cm2，
∵点F是CE的中点，
∴S△BEF＝S△BCE＝×2＝1cm2．
故1．
本题考查了三角形的面积，主要利用了三角形的中线把三角形分成两个面积相等的三角形，原理为等底等高的三角形的面积相等．
18. 规定：logab（a>0，a≠1，b>0）表示a，b之间的一种运算．
现有如下的运算法则：=a，logNM=（n>0，n≠1，N>0，N≠1，M>0）．
例如：log223=3，log25=，则=_________．
【18题答案】
【正确答案】

【详解】===，
故．
三、解 答 题（本大题共10小题，共96分）
19. （1） （2）
（3）（3a+2b）（3a﹣2b）（9a2﹣4b2） （4）用简便方法计算：20152﹣2014×2016
【19题答案】
【正确答案】(1) 0 (2) (3) (4) 1

【详解】试题分析：（1）根据有理数的混合运算进行计算即可；
（2）根据整式的混合运算进行计算即可；
（3）先运用平方差公式，再运用完全平方公式即可得解；
（4）运用平方差公式进行计算即可.
试题解析：（1）原式==2-1-3+2
=0；
（2）原式=-27a9+16a9
=-11a9；
（3）原式=（9a2﹣4b2）2
=;
(4)原式=20152-（2015-1）（2015+1）
=20152-20152+1
=1.
20. 规定一种新运算：＝ad－bc.例如，＝3×6－4×5＝－2，＝4x＋6.按照这种运算规定，当x等于多少时， ＝0.
【20题答案】
【正确答案】5

【分析】根据新运算法则可得(x+1)(x-1)-(x+3)(x-2)=0，解方程可得.
【详解】根据运算法则可得：(x+1)(x-1)-(x+3)(x-2)=0
整理得，x2-1-x2-x+6=0
x=5
故答案为5
理解新运算法则，根据法则列出方程.
21. 先化简，再求值：（y+1）（2y﹣3）﹣（y+1）2﹣2（y﹣1）（其中y2﹣5y=20）
【21题答案】
【正确答案】

【详解】试题分析：原式利用多项式乘以多项式，完全平方式化简，去括号合并得到最简结果，把已知等式代入计算即可求出值．
试题解析：原式=2y2-3y+2y-3-y2-2y-1-2y+2=y2-5y-2，
把y2-5y=20代入得：原式=20-2=18．
22. 如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．
（1）请在图中画出平移后的△A′B′C′；
（2）再在图中画出△A′B′C′的高C′D′，
（3）写出图中与线段AC平行的线段______．并求出△ABC的面积．

【22题答案】
【正确答案】A′C′

【详解】试题解析：（1）根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置，然后顺次连接即可；
（2）根据三角形的高线的定义作出即可；
（3）根据平移的性质找出与线段AC平行的线段，再根据三角形的面积公式列式计算即可得解．
试题解析：（1）△A′B′C′如图所示；

（2）△A′B′C′的高C′D′如图所示；
（3）△ABC的面积=×4×4=8．

23. 如图，在△BCD中，BC=4，BD=5．
（1）求CD的取值范围；
（2）若AE∥BD，∠A=55°，∠BDE=125°，求∠C的度数．

【23题答案】
【正确答案】（1）1