专题3.3 图形变化类规律问题（重点题专项讲练）-七年级数学上册从重点到压轴（北师大版）

这是一份专题3.3 图形变化类规律问题（重点题专项讲练）-七年级数学上册从重点到压轴（北师大版），文件包含专题33图形变化类规律问题重点题专项讲练北师大版解析版docx、专题33图形变化类规律问题重点题专项讲练北师大版原卷版docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。
专题3.3 图形变化类规律问题

【典例1】下列图形是用五角星摆成的，如果按照此规律继续摆下去：

（1）第4个图形需要用 　 　个五角星；第5个图形需要用 　 　个五角星；
（2）第n个图形需要用 　 　个五角星；
（3）用6064个五角星摆出的图案应该是第 　 　个图形；
（4）现有1059个五角星，能否摆成符合以上规律的图形（1059个五角星要求全部用上），请说明理由．
【思路点拨】
（1）不难看出后一个图形比前一个图形多3个五角星，据此进行求解即可；
（2）结合（1）进行分析即可得出结果；
（3）利用（2）中的结论进行求解即可；
（4）利用（2）进行求解即可．
【解题过程】
解：（1）由题意得：第1个图形需要用五角星的个数为：4，
第2个图形需要用五角星的个数为：7＝4+3＝4+3×1，
第3个图形需要用五角星的个数为：10＝4+3+3＝4+3×2，
第4个图形需要用五角星的个数为：13＝4+3+3+3＝4+3×3，
第5个图形需要用五角星的个数为：16＝4+3+3+3+3＝4+3×4，
故答案为：13，16；
（2）由（1）得：第n个图形需要用五角星的个数为：4+3（n﹣1）＝3n+1，
故答案为：（3n+1）；
（3）由题意得：3n+1＝6064，
解得：n＝2021，
故答案为：2021；
（4）不能，理由如下：
由题意得：3n+1＝1059，
解得：n=10583，不是整数，
∴1059个五角星不能摆成符合以上规律的图形．

1．（2022•沙坪坝区校级二模）把黑色圆点按如图所示的规律拼图案，其中第①个图案中有4个黑色圆点，第②个图案中有6个黑色圆点，第③个图案中有8个黑色圆点，…，按此规律排列下去，则第⑦个图案中黑色圆点的个数为（　　）

A．12 B．14 C．16 D．18
【思路点拨】
第①个图案中有4个黑色圆点，第②个图案中有（4+2）个黑色圆点，第③个图案中有（4+2+2）个黑色圆点，则可以总结出第n个图形中黑色圆点的个数，代入n＝7计算即可．
【解题过程】
解：第①个图案中有4个黑色圆点，
第②个图案中有（4+2）个黑色圆点，
第③个图案中有（4+2+2）个黑色圆点，
第④个图案中有（4+2+2+2）个黑色圆点，
……
则第n个图形中黑色圆点的个数为4+2（n﹣1）＝2n+2，
当n＝7时，2n+2＝2×7+2＝16，
∴第⑦个图案中黑色圆点的个数为16．
故选：C．
2．（2022•桐梓县模拟）观察下列树枝分叉的规律图，若第n个图树枝数用Yn表示，则Y9﹣Y4＝（　　）

A．55个 B．65个 C．75个 D．496个
【思路点拨】
第n个图形树枝数为Y，Y随n的变化而变化，则Y＝2n﹣1，代入n＝9和n＝4求代数式的值即可．
【解题过程】
解：第n个图形树枝数为Y，Y随n的变化而变化，
当n＝1时，Y＝21﹣1＝1，
当n＝2时，Y＝22﹣1＝3，
当n＝3时，Y＝23﹣1＝7，
当n＝4时，Y＝24﹣1＝15，
所以第n个图形中树枝的个数Y＝2n﹣1，
Y9﹣Y4＝29﹣1﹣（24﹣1）＝496．
故选：D．
3．（2022•沙坪坝区校级开学）将一些完全相同的梅花按如图所示的规律摆放，第1个图形有5朵梅花，第2个图形有8朵梅花，第3个图形有13朵梅花，…按此规律，则第7个图形中共有梅花的朵数是（　　）

A．39 B．40 C．53 D．68
【思路点拨】
由题意可知：第1个图形有1+4＝5朵梅花，第2个图形有1+2+1+4＝8朵梅花，第3个图形有1+2+3+2+1+4＝13朵梅花，…由此得出第n个图形中共有梅花的朵数是1+2+3+4+…+n+n﹣1+…+4+3+2+1+4＝n2+4，由此代入求得答案即可．
【解题过程】
解：∵第1个图形有1+4＝5朵梅花，
第2个图形有1+2+1+4＝8朵梅花，
第3个图形有1+2+3+2+1+4＝13朵梅花，
…
∴第n个图形中共有梅花的朵数是1+2+3+4+…+n+n﹣1+…+4+3+2+1+4＝n2+4，
则第7个图形中共有梅花的朵数是72+4＝53．
故选：C．
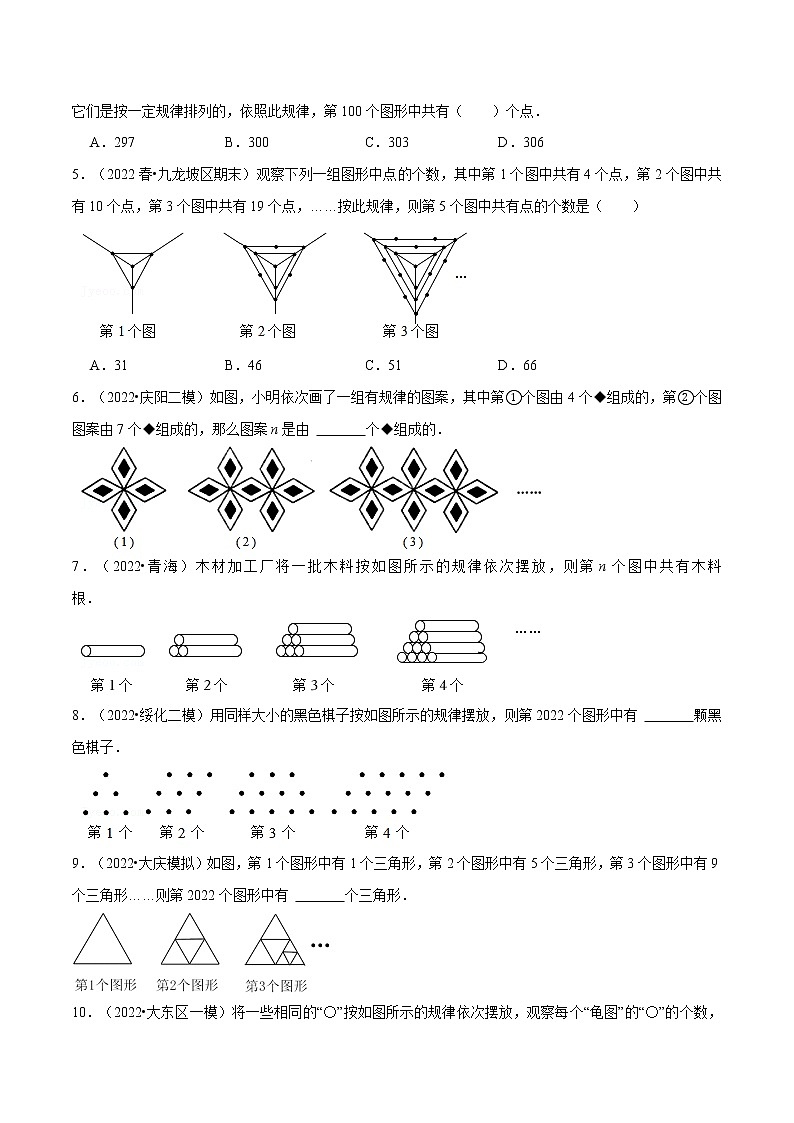
4．（2022•西山区二模）观察下列图形：

它们是按一定规律排列的，依照此规律，第100个图形中共有（　　）个点．
A．297 B．300 C．303 D．306
【思路点拨】
观察图形特点，从中找出规律，它们的点数分别是6，9，12，15，…，总结出其规律，根据规律即可求解．
【解题过程】
解：通过观察，得到点的个数分别是6，9，12，15，…，
第一个图形为：1+2+3＝6，
第二个图形为：1+3+5＝9，
第三个图形为：1+4+7＝12，
第四个图形为：1+5+9＝15，
…，
所以第n个图形为：（3n+3）个点，
当n＝100时，3n+3＝303．
故选：C．
5．（2022春•九龙坡区期末）观察下列一组图形中点的个数，其中第1个图中共有4个点，第2个图中共有10个点，第3个图中共有19个点，……按此规律，则第5个图中共有点的个数是（　　）

A．31 B．46 C．51 D．66
【思路点拨】
由图可知：其中第1个图中共有1+1×3＝4个点，第2个图中共有1+1×3+2×3＝10个点，第3个图中共有1+1×3+2×3+3×3＝19个点，…由此规律得出第n个图有1+1×3+2×3+3×3+…+3n个点．
【解题过程】
解：第1个图中共有1+1×3＝4个点，
第2个图中共有1+1×3+2×3＝10个点，
第3个图中共有1+1×3+2×3+3×3＝19个点，
第4个图中共有1+1×3+2×3+3×3+3×4＝31个点，
…
第n个图有1+1×3+2×3+3×3+…+3n个点．
所以第5个图中共有点的个数是1+1×3+2×3+3×3+4×3+5×3＝46．
故选：B．
6．（2022•庆阳二模）如图，小明依次画了一组有规律的图案，其中第①个图由4个◆组成的，第②个图图案由7个◆组成的，那么图案n是由 　3n+1　个◆组成的．

【思路点拨】
观察不难发现，后一个图案比前一个图案多3个◆，然后写出第n个图案的◆的个数是4+3（n﹣1）＝3n+1．
【解题过程】
解：第1个图案◆的个数为4，
第2个图案◆的个数为7，7＝4+3，
第3个图案◆的个数为10，10＝4+3×2，
…，
第n个图案◆的个数为：4+3（n﹣1）＝3n+1，
故答案为：3n+1．
7．（2022•青海）木材加工厂将一批木料按如图所示的规律依次摆放，则第n个图中共有木料 　n(n+1)2　根．

【思路点拨】
观察图形可得：第n个图形最底层有n根木料，据此可得答案．
【解题过程】
解：由图可知：
第一个图形有木料1根，
第二个图形有木料1+2＝3（根），
第三个图形有木料1+2+3＝6（根），
第四个图形有木料1+2+3+4＝10（根），
.....．
第n个图有木料1+2+3+4+......+n=n(n+1)2（根），
故答案为：n(n+1)2．
8．（2022•绥化二模）用同样大小的黑色棋子按如图所示的规律摆放，则第2022个图形中有 　6069　颗黑色棋子．
【思路点拨】
由图形可知：第1个图形的黑色棋子的个数为6，第2个图形的黑色棋子的个数为6+3＝9，第3个图形的黑色棋子的个数为6+3×2＝12，…由此得出第n个图形的黑色棋子的个数为6+3（n﹣1）＝3n+3，从而可求解．
【解题过程】
解：∵第1个图形的黑色棋子的个数为6，
第2个图形的黑色棋子的个数为6+3＝9，
第3个图形的黑色棋子的个数6+3×2＝12，
…，
∴第n个图形的黑色棋子的个数为6+3（n﹣1）＝3n+3，
∴第2022个图形中黑色棋子的个数为：3×2022+3＝6069．
故答案为：6069．
9．（2022•大庆模拟）如图，第1个图形中有1个三角形，第2个图形中有5个三角形，第3个图形中有9个三角形……则第2022个图形中有 　8085　个三角形．

【思路点拨】
根据题目中的图形，可以发现三角形个数的变化规律：4n﹣3，从而可以解答本题．
【解题过程】
解：第1个图形中一共有1个三角形，
第2个图形中一共有1+4＝5个三角形，
第3个图形中一共有1+4+4＝9个三角形，
…
第n个图形中三角形的个数是1+4（n﹣1）＝4n﹣3，
当n＝2022时，4×2022﹣3＝8085，
∴第2022个图形中有8085个三角形．
故答案为：8085．
10．（2022•大东区一模）将一些相同的“〇”按如图所示的规律依次摆放，观察每个“龟图”的“〇”的个数，则第10个“龟图”中有 　95　个“〇”．

【思路点拨】
分析数据可得：第1个图形中小圆的个数为1+4＝5；第2个图形中小圆的个数为1+5+1＝7；第3个图形中小圆的个数为1+6+4＝11；第4个图形中小圆的个数为1+7+9＝17；…由此得出第n个图形中小圆的个数为1+（n+3）+（n﹣1）2．据此可以求得答案．
【解题过程】
解：∵第1个图形中小圆的个数为1+4＝5；
第2个图形中小圆的个数为1+5+1＝7；
第3个图形中小圆的个数为1+6+4＝11；
第4个图形中小圆的个数为1+7+9＝17；
…
∴第n个图形中小圆的个数为1+（n+3）+（n﹣1）2．
∴第30个“龟图”中的“〇”的个数为1+（30+3）+（30﹣1）2＝1+33+841＝875．
另一种解法：∵第1个图形中小圆的个数为0+5＝5；
第2个图形中小圆的个数为2+5＝1×2+5＝7；
第3个图形中小圆的个数为6+5＝2×3+5＝11；
第4个图形中小圆的个数为12+5＝3×4+5＝17；
…
∴第n个图形中小圆的个数为n（n﹣1）+5．
∴第10个“龟图”中的“〇”的个数为10×（10﹣1）+5＝95．
故答案为：95．
11．（2022•乐陵市模拟）如图所示，将形状大小完全相同的“▱”按照一定规律摆成下列图形，第1幅图中“▱”的个数为a1，第2幅图中“▱”的个数为a2，第3幅图中“▱”的个数为a3，…，以此类推，2022a1+2022a2+2022a3+2022a4+⋯+2022a2021的值为 　2021　．

【思路点拨】
认真读题，由图可知a1＝1×2，a2＝2×3，a3＝3×4，a4＝4×5，......，由此可知an＝n（n+1），问题可求解．
【解题过程】
解：由题意可知图可知a1＝1×2，a2＝2×3，a3＝3×4，a4＝4×5，......，
∴an＝n（n+1），
∴1an=1n(n+1)=1n-1n+1，
∴2022a1+2022a2+2022a3+2022a4+......+2022a2021
＝2022×（1a1+1a2+1a3+1a4+......+1a2021）
＝2022×（1-12+12-13+13-14+14-15+.....+12021-12022）
＝2022×（1-12022）
＝2022﹣1
＝2021．
故答案为：2021．
12．（2021秋•安庆期末）如图，自行车每节链条的长度为2.5cm，交叉重叠部分的圆的直径为0.8cm．

（1）4节链条拉直后长度为 　7.6cm　；
（2）n节链条拉直后长度为 　（1.7n+0.8）cm　；
（3）如果一辆自行车的链条由50节这样的链条首尾环形相连组成，那么该自行车链条环的长度是多少？
【思路点拨】
（1）结合图形直接计算；
（2）从特殊到一般，找到规律列式即可；
（3）在（2）的基础上，注意到环型链条比直线型链条多一个连接的接头，因此长度要少一个圆的直径，即可求解．
【解题过程】
解：（1）根据图形可得，
2节链条的长度为：2.5×2﹣0.8＝4.2 cm，
3节链条的长度为：2.5×3﹣0.8×2＝5.9 cm，
4节链条的长度为：2.5×4﹣0.8×3＝7.6 cm．
故答案为：7.6cm．
（2）由（1）可知，n节链条拉直后的长度为：2.5×n﹣0.8×（n﹣1）＝（1.7n+0.8）cm．
故答案为：（1.7n+0.8）cm．
（3）自行车的链条为环形，比拉直的链条多重叠一个圆的接头，
所以50节自行车链条的长度为：1.7×50+0.8﹣0.8＝85cm．
13．（2021秋•新昌县期末）某学校食堂新购进了一批梯形餐桌，如图1所示，每张桌子可坐5人．

（1）七（2）班41名学生同时就餐，当餐桌按如图2摆放时，至少需要多少张梯形餐桌？
（2）现班级要举办一个活动，计划用4张餐桌无缝拼接，刚好能坐满10个人，请设计一个餐桌摆放的方案，并画出方案示意图．
【思路点拨】
（1）由题意不难得出每增加1张桌子，可坐人数增加3人，据此求解；
（2）根据题意进行设计即可．
【解题过程】
解：（1）由题意得：1张桌子可坐的人数为：5；
2张桌子可坐的人数为：8＝5+3＝5+3×1；
3张桌子可坐的人数为：11＝5+3+3＝5+3×2；
..．
则n张桌子可坐的人数为：5+3（n﹣1）＝3n+2，
∴3n+2＝41，
解得：n＝13，
答：至少需要13张梯形餐桌；
（2）因为用4张餐桌无缝拼接，刚好能坐满10个人，
则其设计方案如图所示：
．
14．（2021秋•金水区校级期末）用火柴棒按如图的方式搭图形．
（1）按图示规律完成下表：
图形标号
①
②
③
④
⑤
…
火柴棒根数
5
9
　13　
　17　
　21　
…
（2）按照这种方式搭下去，搭第n个图形需要多少根火柴棒？
（3）搭第2022个图形需要多少根火柴棒？

【思路点拨】
（1）根据所给的图形进行分析即可得出结果；
（2）由（1）进行总结即可；
（3）根据（2）所得的式子进行解答即可．
【解题过程】
解：（1）第1个图形的火柴棒根数为：5，
第2个图形的火柴棒根数为：9＝5+4＝5+4×1，
第3个图形的火柴棒根数为：13＝5+4+4＝5+4×2，
第4个图形的火柴棒根数为：17＝5+4+4+4＝5+4×3，
第5个图形的火柴棒根数为：21＝5+4+4+4+4＝5+4×4，
……
故答案为：13，17，21；
（2）由（1）得：搭第n个图形需要火柴棒根数为：5+4（n﹣1）＝4n+1．
答：第n个图形需要火柴棒根数为：4n+1；
（3）当n＝2022时，4n+1＝4×2022+1＝8089，
所以搭第2022个图形需要8089根火柴棒．
15．（2021秋•肥西县月考）数学兴趣小组活动上，宇阳同学用围棋棋子按照某种规律摆成如图所示的“100”字样．

（1）按照这种规律，第5个“100”字样的棋子个数是 　31　，第n个“100”字样的棋子个数是 　（5n+6）　；
（2）若有2022个这样的棋子，按这种摆法是否正好摆成一个“100”，若能，求摆出是第几个“100”？若不能，说明理由．
【思路点拨】
（1）根据图形的变化可知，每个图形都比前一个多5个棋子，根据此规律得出第6个图形的棋子数即可；
（2）由（1）的规律归纳出的第n个图形棋子数，列式求解即可判断．
【解题过程】
解：（1）由图知，第1个“100”字样图案的棋子个数是11＝5+6，
第2个“100”字样图案的棋子个数是16＝5×2+6；
第3个“100”字样图案的棋子个数是21＝5×3+6；
…，
第5个“100”字样图案的棋子个数是5×5+6＝31；
第n个“100”字样图案的棋子个数是5n+6；
故答案为：31；（5n+6）；
（2）不能，理由如下：
令5n+6＝2022，
解得n=20165，
因为20165不是整数，
所以不能．
16．（2021秋•长安区期末）将边长相等的黑、白两色小正方形按如图所示的方式拼接起来，第1个图由5个白色小正方形和1个黑色小正方形拼接起来，第2个图由8个白色小正方形和2个黑色小正方形拼接起来，第3个图由11个白色小正方形和3个黑色小正方形拼接起来，依此规律拼接．

（1）第4个图白色小正方形的个数为 　14　；
（2）第10个图白色小正方形的个数为 　32　；
（3）第n个图白色小正方形的个数为 　3n+2　（用含n的代数式表示，结果应化简）；
（4）是否存在某个图形，其白色小正方形的个数为2021个，若存在，求出是第几个图形；若不存在，请说明理由．
【思路点拨】
（1）不难看出，后一个图中的白色小正方形的个数比前一个图中的白色小正方形的个数多3个，据此即可求第4个图中白色小正方形的个数；
（2）根据（1）可先表示出第n个图中白色小正方形的个数，再求第10个图中小正方形的个数即可；
（3）由（2）即可得解；
（4）根据所得到的规律进行求解即可．
【解题过程】
解：（1）由题意得：第4个图中白色小正方形的个数为：11+3＝14（个），
故答案为：14；
（2）∵第1个图有5个白色小小正方形，
第2个图有8个白色小正方形，即8＝5+3＝5+3×1，
第3个图有11个白色小正方形，即11＝5+3+3＝5+3×2，
..．
∴第n个图有白色小正方形的个数为：5+3（n﹣1）＝3n+2，
∴第10个图中小正方形的个数为：3×10+2＝32（个），
故答案为：32；
（3）由（2）得：第n个图有白色小正方形的个数为3n+2，
故答案为：3n+2；
（4）存在，
设第n个图白色小正方形的个数为2021，
则3n+2＝2021，
解得n＝673，
所以第673个图白色小正方形的个数为2021．
17．（2021秋•乐平市期中）如图是用棋子摆成的“上”字图案，按照这种规律继续摆下去，通过观察、对比、总结，找出规律，解答下列问题．

（1）摆成图1需要 　6　枚棋子，摆成图2需要 　10　枚棋子，摆成图3需要 　14　枚棋子；
（2）摆成图n需要 　（4n+2）　枚棋子；
（3）七（1）班有46名同学，把每名同学当成一枚“棋子”，能否让这46枚“棋子”按照以上规律恰好站成一“上”字？若能，请问能站成图几？并计算最下面一“横”的学生数；若不能，请说明理由．
【思路点拨】
（1）根据图形直接数出来即可；
（2）根据（1）得到的规律计算即可；
（3）让（2）得到的代数式等于62求值，求得整数解，进而看在1的基础上增加几个2即可．
【解题过程】
解：（1）第①个图形中有6个棋子；
第②个图形中有6+4＝10个棋子；
第③个图形中有6+2×4＝14个棋子；
故答案为：6，10，14；
（2）∵第①个图形中有6个棋子，6＝6+4×0；
第②个图形中有10个棋子，10＝6+4×1；
第③个图形中有14个棋子，14＝6+4×2；
∴第n个图形中有6+（n﹣1）×4＝4n+2．
故答案为：（4n+2）．
（3）能，理由如下：
4n+2＝46，
解得n＝11．
最下一横人数为2n+1＝23．
18．（2021秋•连云港月考）下列是用火柴棒拼出的一列图形．

仔细观察，找出规律，解答下列各题：
（1）第6个图中共有 　19　根火柴；
（2）第n个图形中共有 　（3n+1）　根火柴；（用含n的式子表示）
（3）第2021个图形中共有多少根火柴？
【思路点拨】
（1）根据图形的变化直接得出第6个图中火柴棒的数量即可；
（2）根据图形的变化规律得出第n个图形中有3n+1根火柴即可；
（3）根据（2）的规律直接计算即可．
【解题过程】
解：（1）由图知，
第1个图中火柴棒的数量为3+1＝4（根），
第2个图中火柴棒的数量为2×3+1＝7（根），
第3个图中火柴棒的数量为3×3+1＝10（根），
第4个图中火柴棒的数量为4×3+1＝13（根），
第5个图中火柴棒的数量为5×3+1＝16（根），
第6个图中火柴棒的数量为6×3+1＝19（根），
故答案为：19；
（2）由（1）可得，
第n个图中火柴棒的数量为（3n+1）根，
故答案为：（3n+1）；
（3）由（2）知，第2021个图形中火柴棒的数量为2021×3+1＝6064（根），
∴第2021个图形中共有6064根火柴．
19．（2021秋•安次区校级期中）如图是用长度相等的小棒按一定规律摆成的一组图案．

（1）第1个图案中有6根小棒；第2个图案中有 　11　根小棒；第3个图案中有 　16　根小棒；
（2）第n个图案中有 　（5n+1）　根小棒；
（3）第45个图案中有 　226　根小棒；
（4）是否存在某个符合上述规律的图案，由2032根小棒摆成？如果有，指出是第几个图案；如果没有，请说明理由．
【思路点拨】
（1）由图可知：第①个图案中有5+1＝6根小棒，第②个图案中有2×5+2﹣1＝11根小棒，第③个图案中有3×5+3﹣2＝16根小棒；
（2）由此得出第n个图案中有5n+n﹣（n﹣1）＝5n+1根小棒；
（3）把数据代入（2）中的规律求得答案即可；
（4）利用（2）中的规律建立方程求得答案即可．
【解题过程】
解：（1）第②个图案中有11根小棒；第③个图案中有16根小棒，
故答案为：11、16；
（2）由图可知：第①个图案中有5+1＝6根小棒，
第②个图案中有2×5+2﹣1＝11根小棒，
第③个图案中有3×5+3﹣2＝16根小棒，
…，
因此第n个图案中有小棒的根数为：5n+n﹣（n﹣1）＝5n+1．
故答案为：（5n+1）；
（3）当n＝45时，5n+1＝5×45+1＝226，
所以第25个图案中有126根小棒；
故答案为：226；
（4）不存在，理由如下：
∵5n+1＝2032，
∴n＝406.2；
所以不存在由2032根小棒摆成的图案．
20．（2021秋•金水区校级期末）下图是由边长相同的小正方形组成的，其中部分小正方形涂有阴影，依此规律完成此题．

图形标号
第一个
第二个
第三个
第四个
涂有阴影的小正方形的个数
5
a
13
b
（1）a＝　9　，b＝　17　；
（2）按照这种规律继续下去，则第n个图形中涂有阴影的小正方形的个数为 　4n+1　；（用含n的代数式来表示）；
（3）按照这种规律继续下去，用（2）中的代数式求第2021个图形中涂有阴影的小正方形的个数．
【思路点拨】
（1）根据所给的图形进行分析即可求解；
（2）根据所给的图形分析出规律即可；
（3）利用（2）中的规律进行求解即可．
【解题过程】
解：（1）第1个图形中涂有阴影的小正方形的个数为：5，
第2个图形中涂有阴影的小正方形的个数为：9，
第3个图形中涂有阴影的小正方形的个数为：13，
第4个图形中涂有阴影的小正方形的个数为：17，
故a＝9，b＝17，
故答案为：9，17；
（2）∵第1个图形中涂有阴影的小正方形的个数为：5，
第2个图形中涂有阴影的小正方形的个数为：9＝5+4＝5+4×1，
第3个图形中涂有阴影的小正方形的个数为：13＝5+4+4＝5+4×2，
第4个图形中涂有阴影的小正方形的个数为：17＝5+4+4+4＝5+4×3，
...，
∴第n图形中涂有阴影的小正方形的个数为：5+4（n﹣1）＝4n+1，
故答案为：4n+1；
（3）第2021个图形中涂有阴影的小正方形的个数为：4×2021+1＝4084+1＝4085（个）．
21．（2022•马鞍山二模）观察图：
下列每一幅图都是由一些单位长度均为1的黑方格和白方格按一定的规律组成（下面所有方格均指的单位为1的小方格）．
（1）根据规律，第4个图中共有 　45　个方格，其中黑方格 　12　个．
（2）第n个图形中，白方格共有 　（7n+5）　个．（用n表示，n为正整数）
（3）有没有可能黑方格比白方格恰好少2022个，如果有，求出是第几个图形；如果没有，请说明理由．

【思路点拨】
（1）根据题意归纳出本题第n个图中共有（5+10n）个方格，其中黑方格3n块，再将n＝4代入计算即可；
（2）根据题意归纳出本题第n个图形中共有白方格个数为7n+5．
【解题过程】
解：（1）∵第1个图中共有15＝5+10×1个方格，其中黑方格3＝3×1块，
第2个图中共有25＝5+10×2个方格，其中黑方格6＝3×2块，
第3个图中共有35＝5+10×3个方格，其中黑方格9＝3×3块，
……，
∴第n个图中共有5+10n个方格，其中黑方格3n块，
∴第4个图中共有5+10×4＝45个方格，其中黑方格3×4＝12块，
故答案为：45，12；
（2）∵第1个图形中白方格个数共有：12＝5（1+2×1）﹣3×1，
第2个图形中白方格个数共有：19＝5（1+2×2）﹣3×2，
第3个图形中白方格个数共有：26＝5（1+2×3）﹣3×3，
……，
∴第n个图形中白方格个数共有：5（1+2n）﹣3n＝7n+5，
故答案为：（7n+5）；
（3）没有可能黑方格比白方格恰好少2022个，
设第n个图形黑方格比白方格恰好少2022个，
得3n+2022＝7n+5，
解得n＝504.25，
不符合实际，
∴没有可能黑方格比白方格恰好少2022个．
22．（2022•包河区一模）如图，某学校准备新建一个读书长廊，并用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地砖搭配在一起，按图中所示的规律拼成图案铺满长廊，已知每个小正方形地砖的边长均为0.5米．
（1）按图示规律，第3图案的长度L3＝　3.5米　；第3个图案中没有花纹的正方形地砖数为 　18块　；
（2）若某个图案中带有花纹的地砖为n块，则没有花纹的地砖为 　（5n+3）　块（用含n的代数式表示）；
（3）若学校读书长廊的长度为Ln＝100.5米，求没有花纹的正方形地砖有多少块．

【思路点拨】
（1）观察题目中的已知图形，可知后一个图案的地面长度依次比前一图案的地面长度多1米，没有花纹的正方形地砖数依次比前一图案的没有花纹的正方形地砖数多5个，根据这个规律进行解答便可；
（2）观察题目中的已知图形，可知带有花纹的地砖数与图案的序号数相等，根据不带花纹的地砖数与图案的序号数的关系写出代数式便可；
（3）观察题目中的已知图形，得到图案的地面长度与图案序号数的关系，求出n的值，再根据不带花纹的地砖数与图案的序号数的关系求得结果．
【解题过程】
解：（1）观察图案可知，后一个图案的地面长度依次比前一图案的地面长度多1米，
∴第3图案的长度L3＝3×0.5+1+1＝3.5（米），
∵观察图案可知，后一个图案没有花纹的正方形地砖数依次比前一图案的没有花纹的正方形地砖数多5个，
∴第3个图案中没有花纹的正方形地砖数为：8+5+5＝18（块），
故答案为：3.5米；18块；
（2）观察可得：第1个图案中有花纹的地面砖有1块，第2个图案中有花纹的地面砖有2块，…
故第n个图案中有花纹的地面砖有n块，
∵某个图案中带有花纹的地砖为n块，
∴这个图案是第n个图案，
观察可得：第1个图案中没有花纹的地面砖有5+3＝8块，第2个图案中没有花纹的地面砖有5×2+3＝13块，第3个图案中没有花纹的地面砖有5×3+3＝18块，…
故第n个图案中没有花纹的地面砖有5n+3块；
故答案为：（5n+3）；
（3）观察可知，第1图案的长度为：（2×1+1）×0.5米，第2图案的长度为：（2×2+1）×0.5米，第3图案的长度为：（2×3+1）×0.5米，…
故第n图案的长度为：0.5（2n+1）米，
∵学校读书长廊的长度为Ln＝100.5米，
∴0.5（2n+1）＝100.5，
解得，n＝100，
∴学校读书长廊没有花纹的正方形地砖数为：5n+3＝503（块），
答：学校读书长廊没有花纹的正方形地砖503块．