初中人教版18.1.2 平行四边形的判定教学演示课件ppt

这是一份初中人教版18.1.2 平行四边形的判定教学演示课件ppt，共24页。
B 解析：∵E是BC的中点，∴CE＝BE.∵∠B＝∠BCF，∠BED＝∠CEF，∴△CEF≌△BED(ASA)，∴CF＝BD.∵D是AB的中点，∴AD＝BD，∴AD＝CF.∵∠B＝∠BCF，∴AD∥CF，∴四边形ADFC为平行四边形.
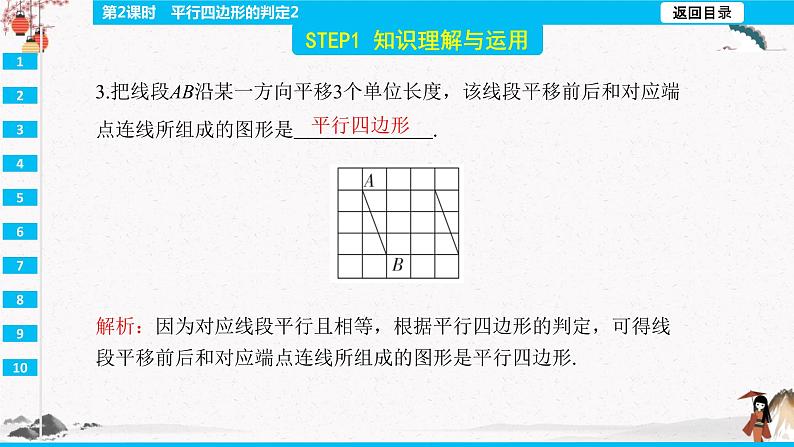
平行四边形 解析：因为对应线段平行且相等，根据平行四边形的判定，可得线段平移前后和对应端点连线所组成的图形是平行四边形.
4.已知四边形ABCD中，AB∥CD，AB＝CD，周长为40 cm，两邻边的比是3∶2，则较长边的长度是　　　　　.
12 cm 解析：∵AB∥CD，AB＝CD，∴四边形ABCD是平行四边形，∴AD＝BC.设平行四边形ABCD的两邻边长分别是3x，2x.∵平行四边形ABCD的周长是40 cm，∴2(3x＋2x)＝40，解得x＝4，∴较长边的长度是3×4＝12(cm).
知识点六　 平行四边形的性质与判定的综合5.下列条件中，能判定一个四边形是平行四边形的是( )A.一组对边平行，另一组对边相等B.一组对边平行，一组对角相等C.一组邻边相等，一组对角相等D.一组对边平行，一组对角互补
B 解析：A.一组对边平行，另一组对边相等，可能是等腰梯形，不一定是平行四边形，故选项A不符合题意；B.一组对边平行，一组对角相等，可得到两组对边分别平行，是平行四边形，故选项B符合题意；C.由一组邻边相等，一组对角相等，不能判定一个四边形是平行四边形，故选项C不符合题意；D.一组对边平行，一组对角互补，可能是等腰梯形，不一定是平行四边形，故选项D不符合题意.
6.顺次连接平面上A，B，C，D四点得到一个四边形，从① AB∥CD；②BC＝AD；③∠A＝∠C；④∠B＝∠D四个条件中任选其中两个，不能得出“四边形ABCD是平行四边形”这一结论的是( )A.①②　 　B.①③　　 C.①④　 　D.③④
D 解析：∵D，E分别为AC，BC的中点，∴DE是△ABC的中位线，∴AB＝2DE.∵DE＝12 m，∴AB＝24 m.
B 解析：∵D，E分别是AB，BC的中点，∴DE是△ABC的中位线，∴DE∥AC，∴∠DEB＝∠C＝44°.
∴△AGE≌△CHE(AAS)，∴AG＝HC.∵AG∥BC，AB∥GH，∴四边形ABHG为平行四边形，∴AG＝BH，∴BH＝HC，∴四边形ABHG的周长＝2AB＋2BH.∵△ABC的周长＝AB＋AC＋BC＝AB＋AC＋2BH，∴当AB＝AC时，四边形ABHG的周长与△ABC的周长相等.