2023年中考数学模拟试卷强化练习卷一（含答案）

这是一份2023年中考数学模拟试卷强化练习卷一（含答案），共10页。试卷主要包含了选择题，填空题，计算题，作图题，解答题，综合题等内容，欢迎下载使用。

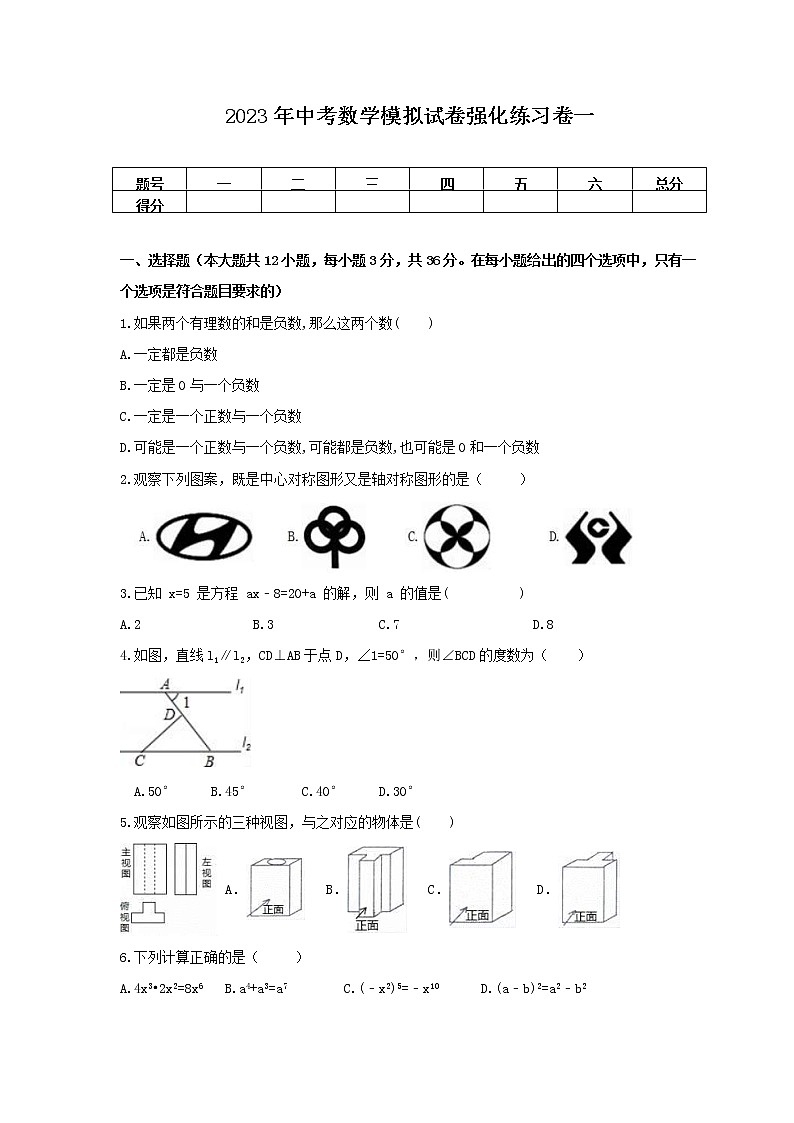
一、选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一个选项是符合题目要求的）
如果两个有理数的和是负数,那么这两个数( )
A.一定都是负数
B.一定是0与一个负数
C.一定是一个正数与一个负数
D.可能是一个正数与一个负数,可能都是负数,也可能是0和一个负数
观察下列图案，既是中心对称图形又是轴对称图形的是（ ）

已知 x=5 是方程 ax﹣8=20+a 的解，则 a 的值是( )
A.2 B.3 C.7 D.8
如图，直线l1∥l2，CD⊥AB于点D，∠1=50°，则∠BCD的度数为（ ）
A.50° B.45° C.40° D.30°
观察如图所示的三种视图，与之对应的物体是( )
A． B． C． D．
下列计算正确的是（ ）
A.4x3•2x2=8x6 B.a4+a3=a7 C.(﹣x2)5=﹣x10 D.(a﹣b)2=a2﹣b2
二次函数y=(x﹣1)2+2的最小值是( )
A.2 B.1 C.﹣1 D.﹣2
某射击运动员在训练中射击了10次，成绩如图所示：
下列结论不正确的是( )
A．众数是8 B．中位数是8 C．平均数是8.2 D．方差是1.2
在给定的条件中，能作出平行四边形的是( )
A.以60cm为对角线，20cm、34cm为两条邻边
B.以20cm、36cm为对角线，22cm为一条边
C.以6cm为一条对角线，3cm、10cm为两条邻边
D.以6cm、10cm为对角线，8cm为一条边
若反比例函数y＝eq \f(k,x)的图象经过点(2，－1)，则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
如图，已知点P是双曲线y=上的一个动点，连结OP，若将线段OP绕点O逆时针旋转90°得到线段OQ，则经过点Q的双曲线的表达式为( )
A.y= B.y=﹣ C.y= D.y=﹣
从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中.
观察得出了下面五条信息：
①abc＜0；②a+b+c＜0；③b+2c＞0；④4ac﹣b2＞0；⑤2a=3b.
你认为其中正确信息的个数有( )
A.2 B.3 C.4 D.5
二、填空题（本大题共6小题，每小题3分，共18分）
分解因式(a－b)(a－4b)＋ab的结果是 .
在一个不透明的布袋中，红色、黑色、白色的球共有20个，除颜色外，形状、大小、质地等完全相同，小明通过大量摸球试验后发现摸到红色、黑色球的频率分别稳定在10%和30%，则口袋中白色球的个数很可能是 个.
甲、乙两人加工同一零件，每小时甲比乙多加工5个，甲加工120个零件与乙加工100个零件所用时间相同，求甲和乙每小时各加工多少个零件？若设甲每小时加工零件x个，则可列方程 .
如图，矩形ABCD中，点E是边AD的中点，BE交对角线AC于点F，则△AFE与△BCF面积比等于 ．
如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以点A为圆心，AC的长为半径作交AB于点E，以点B为圆心，BC的长为半径作交AB于点D，则阴影部分的面积为 ．
如图，在△ABC中，AD、BE分别是边BC、AC上的中线，AB=AC=5，cs∠C=eq \f(4,5)，那么GE= .
三、计算题（本大题共1小题，共6分）
解方程组：
四、作图题（本大题共1小题，共6分）
如图，在平面直角坐标系中，A(﹣1，5)，B(﹣1，0)，C(﹣4，3).
(1)求出△ABC的面积；
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1；
(3)写出点A1，B1，C1的坐标.
五、解答题（本大题共4小题，共42分）
某校开发了“书画、器乐、戏曲、棋类”四大类兴趣课程．为了解全校学生对每类课程的选择情况，随机抽取了若干名学生进行调查(每人必选且只能选一类)，先将调查结果绘制成如下两幅不完整的统计图：
(1)本次随机调查了多少名学生？
(2)补全条形统计图中“书画”、“戏曲”的空缺部分；
(3)若该校共有1200名学生，请估计全校学生选择“戏曲”类的人数；
(4)学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”，用树形图或列表法求处恰好抽到“器乐”和“戏曲”类的概率．(书画、器乐、戏曲、棋类可分别用字幕A，B，C，D表示)
生态公园计划在园内的坡地上造一片有A，B两种树的混合林，需要购买这两种树苗2000棵，种植A，B两种树苗的相关信息如表.
设购买A种树苗x棵，造这片林的总费用为y元，解答下列问题：
(1)写出y(元)与x(棵)之间的函数关系式；
(2)假设这批树苗种植后成活1960棵，则造成这片林的总费用需多少元？
如图，在平面直角坐标系中，点A坐标为(3，﹣2)，直线l解析式为：y=kx﹣2﹣3k(k≠0)，反比例函数y=﹣eq \f(2,x)上有两点M，N，若点M，N的纵坐标分别为2，1.
(1)当k=﹣1时，一次函数的解析式为 ，并直接在坐标系中画出直线l；
(2)通过计算说明：点A在直线l上；
(3)y=﹣eq \f(2,x)(x＞0)图象上M，N两点及之间的部分记为G，若图象G与直线l有共公点，求k的取值范围.
如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD=CB，延长CD交BA的延长线于点E．
（1）求证：CD为⊙O的切线；
（2）求证：∠C=2∠DBE；
（3）若EA=AO=2，求图中阴影部分的面积．（结果保留π）
六、综合题（本大题共1小题，共12分）
如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，且AB=3，BC=2eq \r(3)，
直线y=eq \r(3)x-2eq \r(3)经过点C，交y轴于点G．
(1)点C、D的坐标；
(2)求顶点在直线y=eq \r(3)x-2eq \r(3)上且经过点C、D的抛物线的解析式；
(3)将(2)中的抛物线沿直线y=eq \r(3)x-2eq \r(3)平移，平移后的抛物线交y轴于点F，顶点为点E．
平移后是否存在这样的抛物线，使△EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请明理由．
\s 0 参考答案
答案为：D
C
C
答案为：D
答案为：C
答案为：A
D
C
D
答案为：D.
答案为：B
二、填空题
答案为：(a－2b)2.
答案为：12.
答案为：=.
答案为：eq \f(1,4).
答案为：π﹣2．
答案为：.
三、计算题
解：x=－1,y=2.
四、作图题
解：(1)如图所示：△ABC的面积：eq \f(1,2)×3×5=7.5；
(2)如图所示：
(3)A1(1，5)，B1(1，0)，C1(4，3).
五、解答题
解：
(1)本次随机调查的学生人数为30÷15%=200(人)；
(2)书画的人数为200×25%=50(人)，戏曲的人数为200﹣(50+80+30)=40(人)，
补全图形如下：
(3)估计全校学生选择“戏曲”类的人数约为1200×=240(人)；
(4)列表得：
∵共有12种等可能的结果，其中恰好抽到“器乐”和“戏曲”类的有2种结果，
∴恰好抽到“器乐”和“戏曲”类的概率为=．
解：(1)y=(15+3)x+(20+4)(2000﹣x)=18x+48000﹣24x=﹣6x+48000；
(2)由题意，可得0.95x+0.99(2000﹣x)=1960，
∴x=500.
当x=500时，y=﹣6×500+48000=45000，
∴造这片林的总费用需45000元.
解：(1)当k=﹣1时，y=﹣x+1，函数图形如图所示：
故答案为y=﹣x+1.
(2)当x=3时，y=3k﹣2﹣3k=﹣2，∴点A在直线l上.
(3)对于反比例函数y=﹣eq \f(2,x)，
当y=2时，x=﹣1，
当y=1时，x=﹣2，
∴M(﹣1，2)，N(﹣2，1)，[来源：Z,xx,k.Cm]
当点M在直线l上时，
2=﹣k﹣2﹣3k，k=﹣1，
当点N在直线l上时，
1=﹣2k﹣2﹣3k，k=﹣eq \f(3,5).
∴满足条件的k的范围为：﹣1≤k≤﹣eq \f(3,5).
解：
（1）证明：连接OD，
∵BC是⊙O的切线，∴∠ABC=90°，
∵CD=CB，∴∠CBD=∠CDB，
∵OB=OD，∴∠OBD=∠ODB，
∴∠ODC=∠ABC=90°，即OD⊥CD，
∵点D在⊙O上，∴CD为⊙O的切线；
（2）证明：如图，∠DOE=∠ODB+∠OBD=2∠DBE，
由（1）得：OD⊥EC于点D，
∴∠E+∠C=∠E+∠DOE=90°，∴∠C=∠DOE=2∠DBE；
（3）解：作OF⊥DB于点F，连接AD，
由EA=AO可得：AD是Rt△ODE斜边的中线，
∴AD=AO=OD，∴∠DOA=60°，∴∠OBD=30°，
又∵OB=AO=2，OF⊥BD，∴OF=1，BF=，
∴BD=2BF=2，∠BOD=180°﹣∠DOA=120°，
∴S阴影=S扇形OBD﹣S△BOD=﹣×2×1=﹣．
六、综合题
解：(1)令y=2eq \r(3)，2eq \r(3)=y=eq \r(3)x-2eq \r(3)，解得x=4，则OA=4﹣3=1，
∴C(4，2eq \r(3))，D(1，2eq \r(3))；
(2)由二次函数对称性得，顶点横坐标为=2.5，
令x=eq \f(5,2)，则y=eq \r(3)×eq \f(5,2)﹣2eq \r(3)=eq \f(\r(3),2)，∴顶点坐标为(eq \f(5,2)，eq \f(\r(3),2))，
∴设抛物线解析式为y=a(x﹣eq \f(5,2))2﹣eq \f(\r(3),2)，把点D(1，2eq \r(3))代入得，a=eq \f(2\r(3),3)，
∴解析式为y=eq \f(2\r(3),3)(x﹣eq \f(5,2))2﹣eq \f(\r(3),2)；
(3)设顶点E在直线上运动的横坐标为m，则E(m，eq \r(3)m﹣2eq \r(3))(m＞0)
∴可设解析式为y=eq \f(2\r(3),3)(x﹣m)2﹣eq \r(3)m﹣2eq \r(3)，
①当FG=EG时，FG=EG=2m，则F(0，2m﹣2eq \r(3))，
代入解析式得：eq \f(2\r(3),3)m2﹣eq \r(3)m﹣2eq \r(3)=2m﹣2eq \r(3)，
得m=0(舍去)，m=eq \r(3)﹣eq \f(3,2)，
此时所求的解析式为：y=eq \f(2\r(3),3)(x﹣eq \r(3)﹣eq \f(3,2))2﹣3﹣eq \f(7,2)eq \r(3)；
②当GE=EF时，FG=2eq \r(3)m，则F(0，2eq \r(3)m﹣2eq \r(3))，
代入解析式得：eq \f(2\r(3),3)m2﹣eq \r(3)m﹣2eq \r(3)=2eq \r(3)m﹣2eq \r(3)，解得m=0(舍去)，m=eq \f(3,2)，
此时所求的解析式为：y=eq \f(2\r(3),3)(x﹣eq \f(3,2))2﹣eq \f(\r(3),2)；
③当FG=FE时，不存在．
题号
一
二
三
四
五
六
总分
得分
单价(元/棵)
成活率
劳务费(元/棵)
A
15
95%
3
B
20
99%
4