陕西省咸阳市2022-2023学年高二上学期期末文科数学试题（含答案）

2022~2023学年度第一学期期末教学质量检测高二

数学（文科）试题

注意事项：

1.本试题共4页，满分150分，时间120分钟.

2.答卷前，考生务必将自己的姓名和准考证号填写在答题卡上.

3.回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.

4.考试结束后，监考员将答题卡按顺序收回，装袋整理；试题不回收.

第I卷（选择题共60分）

一､选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.命题“”的否定是（    ）

A.    B.

C.    D.

2.已知函数可导，且，则（    ）

A.6    B.3    C.0    D.

3.在等比数列中，若，则（    ）

A.3或    B.或9    C.3    D.9

4.已知，则下列大小关系正确的是（    ）

A.    B.

C.    D.

5.已知，若，则的最大值为（    ）

A.    B.    C.    D.1

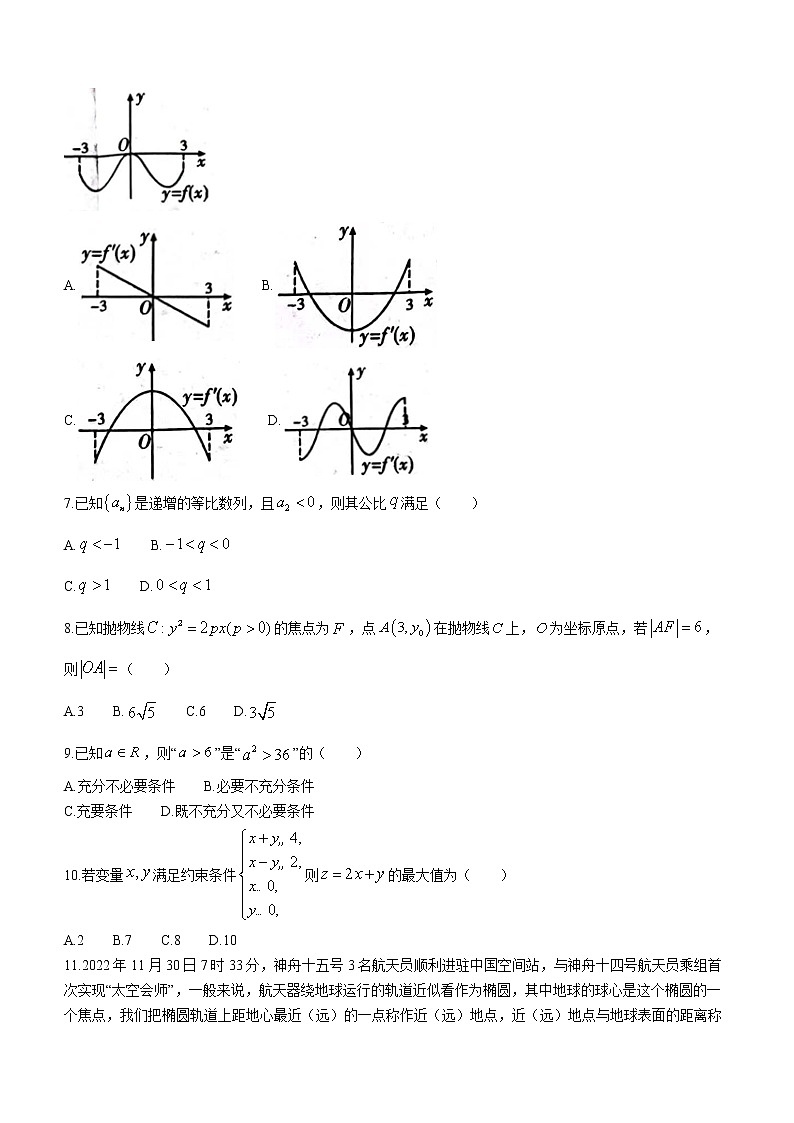
6.已知函数的图像如图所示，则其导函数的图像可能是（    ）

A.    B.

C.    D.

7.已知是递增的等比数列，且，则其公比满足（    ）

A.    B.

C.    D.

8.已知抛物线的焦点为，点在抛物线上，为坐标原点，若，则（    ）

A.3    B.    C.6    D.

9.已知，则“”是“”的（    ）

A.充分不必要条件    B.必要不充分条件

C.充要条件    D.既不充分又不必要条件

10.若变量满足约束条件则的最大值为（    ）

A.2    B.7    C.8    D.10

11.2022年11月30日7时33分，神舟十五号3名航天员顺利进驻中国空间站，与神舟十四号航天员乘组首次实现“太空会师”，一般来说，航天器绕地球运行的轨道近似看作为椭圆，其中地球的球心是这个椭圆的一个焦点，我们把椭圆轨道上距地心最近（远）的一点称作近（远）地点，近（远）地点与地球表面的距离称为近（远）地点高度.已知中国空间站在一个椭圆轨道上飞行，它的近地点高度约为351，远地点高度约为385，地球半径约为6400，则该轨道的离心率约为（    ）

A.    B.    C.    D.

12.已知函数及其导函数，若存在使得，则称是的一个“巧值点”，下列选项中没有“巧值点”的函数是（    ）

A.    B.

C.    D.

第II卷（非选择题共90分）

二､填空题（本大题共4小题，每小题5分，共20分）

13.椭圆的焦点坐标是__________.

14.写出一个离心率为的双曲线方程为__________.

15.已知命题是假命题，则实数的取值范围是__________.

16.《墨经·经说下》中有这样一段记载：“光之人，煦若射，下者之人也高，高者之人也下，足蔽下光，故成景于上；首蔽上光，故成影于下.在远近有端，与于光，故景库内也.”这是中国古代对小孔成像现象的第一次描述.如图为一次小孔成像实验，若物距：像距，则像高为__________.

三､解答题（本大题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤）

17.（本小题满分10分）

设函数.

（1）当时，求不等式的解集；

（2）若关于的不等式的解集为，求实数的取值范围.

18.（本小题满分12分）

已知是等差数列，.

（1）求的通项公式及前项和；

（2）若等比数列满足，求的通项公式.

19.（本小题满分12分）

已知函数在处有极值.

（1）求实数的值；

（2）求函数在上的最值.

20.（本小题满分12分）

在三角形中，内角所对的边分别为，且.

（1）求；

（2）若为锐角，边上的中线，求三角形的面积.

21.（本小题满分12分）

已知椭圆的左，右焦点分别为，离心率为.

（1）求椭圆的方程；

（2）椭圆上是否存在点使得？若存在，求的面积，若不存在，请说明理由.

22.（本小题满分12分）

已知函数.

（1）若，求曲线在处的切线方程；

（2）若，证明：在上只有一个零点.

2022~2023学年度第一学期期末教学质量检测

高二数学（文科）试题参考答案及评分标准

一､选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.C    2.A    3.C    4.B    5.A    6.D    7.D    8.D    9.A    10.B    11.A    12.D

二､填空题（本大题共4小题，每小题5分，共20分）

13.    14.（答案不唯一）    15.    16.

三､解答题（本大题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤）

17.解：（1）当时，不等式，即，即，

即，解得或.

当时，不等式的解集为或.

（2）当时，，符合题意；

当时，由解得.

综上，实数的取值范围是.

18.解：（1）设等差数列的公差为，则，即，

，

..

（2）由（1）知，

设等比数列的公比为，可得，

的通项公式为.

19.解：（1），

.

解得

（2））由（1）知，，

，

若，则；若，则或.

在上单调递增，在上单调递减.

又，

.

20.解：（1），

.

，即，

，

，

或.

（2）为锐角，，

为等腰三角形，且.

在中，设，则.

在中，由余弦定理得.

，解得.

.

.

21.解：（1）椭圆的离心率为，

，解得.

椭圆的方程为.

（2）由（1）知，

假设椭圆上存在点，使得，

则，

即，

联立解得.

椭圆上存在点使得.

.

（注：学生若用其他方法作答，只要解答正确，可参照给分）

22.解：（1）当时，，

.

.

所求切线方程为，即.

（2）证明：由，变形可得，

当时，，则函数只有一个零点等价于函数只有一个零点，可得，

又由，则，

即在上单调递增，

又在上只有一个零点，

即函数在上只有一个零点.