北师大版九年级下册1 圆背景图ppt课件

这是一份北师大版九年级下册1 圆背景图ppt课件，共24页。PPT课件主要包含了复习引入，①角的顶点在圆上，情境引入，直径所对应的圆周角，典例精析，练一练，圆内接四边形及其性质，性质探究，试一试，根据圆周角定理可知等内容，欢迎下载使用。
问题 1 什么是圆周角？
② 角的两边都与圆相交.
顶点在圆上，并且两边都和圆相交的角叫圆周角.
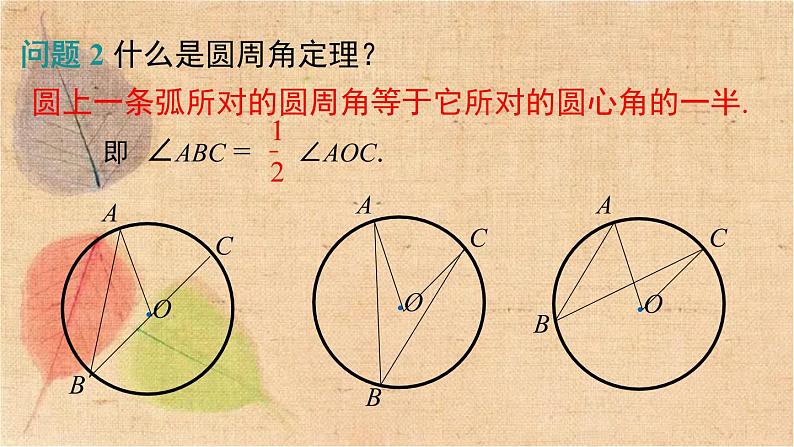
问题 2 什么是圆周角定理？
圆上一条弧所对的圆周角等于它所对的圆心角的一半.
如图是一个圆形笑脸，给你一个三角板，你有办法确定这个圆形笑脸的圆心吗？
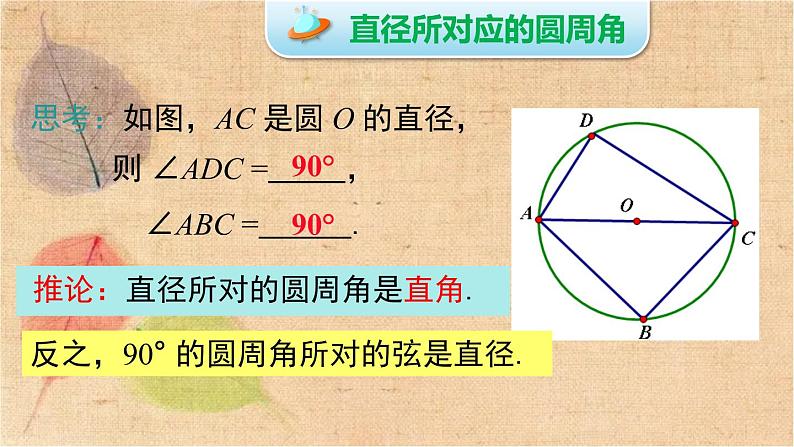
思考：如图，AC 是圆 O 的直径，
则 ∠ADC = ， ∠ABC = .
推论：直径所对的圆周角是直角.
反之，90° 的圆周角所对的弦是直径.
问题 回归到最初的问题，你能确定圆形笑脸的圆心吗？
利用三角板在圆中画出两个 90° 的圆周角，这样就得到两条直径，那么这两条直径的交点就是圆心.
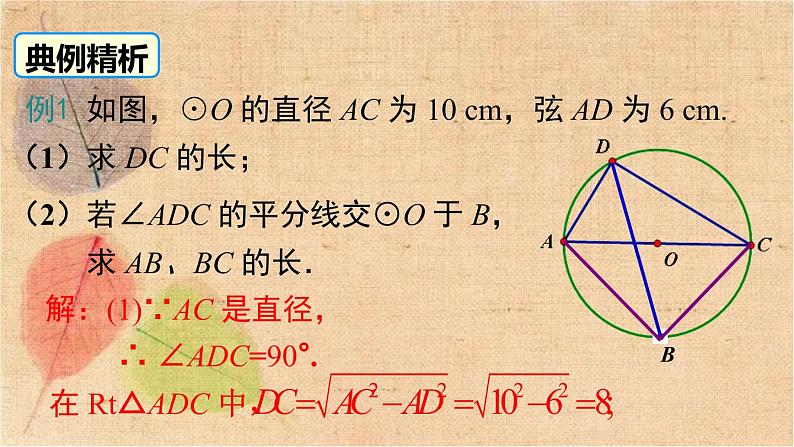
例1 如图，⊙O 的直径 AC 为 10 cm，弦 AD 为 6 cm.（1）求 DC 的长；
（2）若∠ADC 的平分线交⊙O 于 B， 求 AB、BC 的长．
在 Rt△ABC 中,AB 2+BC 2=AC 2，
(2)∵ AC 是直径,∴ ∠ABC=90°. ∵BD 平分∠ADC,∴∠ADB=∠CDB. 又∵∠ACB=∠ADB ,∠BAC=∠BDC . ∴ ∠BAC=∠ACB, ∴AB=BC.
如图，BD 是 ⊙O 的直径，∠CBD＝30°，则∠A 的度数为(　　)A．30° B．45° C．60° D．75°
解析：∵BD 是 ⊙O 的直径，∴∠BCD＝90°.∵∠CBD＝30°，∴∠D＝60°，∴∠A＝∠D＝60°.故选 C.
四边形的四个顶点都在同一个圆上，像这样的四边形叫做圆内接四边形，这个圆叫做四边形的外接圆.
思考：圆内接四边形有什么特殊的性质吗？
如图，四边形 ABCD 为☉O 的内接四边形，☉O 为四边形 ABCD 的外接圆.
(2) 当 ABCD 为一般四边形时，猜想：∠A 与∠C, ∠B 与∠D 之间的关系为 .
∠A+∠C=180º，∠B+∠D=180º
(1) 当 ABCD 为矩形时，∠A 与∠C, ∠B与∠D 之间的关系为 .
证明：圆内接四边形的对角互补.
已知，如图，四边形 ABCD 为 ☉O 的内接四边形，☉O为四边形 ABCD 的外接圆. 求证∠BAD+∠BCD=180°.
证明：连接 OB、OD.
由四边形内角和定理可知，∠ABC+∠ADC=180°
圆内接四边形的对角互补.
∵∠A＋∠DCB＝180°，
∠DCB＋∠DCE＝180°.
如图，∠DCE 是圆内接四边形 ABCD 的一个外角，∠A 与 ∠DCE 的大小有何关系？
1. 四边形 ABCD 是 ⊙O 的内接四边形，且 ∠A=110°， ∠B=80°，则 ∠C= ，∠D= .2. ⊙O 的内接四边形 ABCD 中， ∠A∶∠B∶∠C = 1∶2∶3 ，则∠D= .
解析：∵∠BOD＝120°， ∴∠A＝60°， ∴∠C＝180°－60°＝120°，故选A.
3. 如图，在 ⊙O 的内接四边形 ABCD 中，∠BOD＝120°，那么 ∠BCD 是(　　)A．120° B．100°C．80° D．60°
例2 如图，AB 为 ⊙O 的直径，CF⊥AB于E，交⊙O 于 D，AF 交 ⊙O 于G. 求证：∠FGD＝∠ADC.
证明：∵四边形 ACDG 内接于 ⊙O，∴∠FGD＝∠ACD.又∵AB 为 ⊙O 的直径，CF⊥AB 于E，∴AB垂直平分CD，∴AC＝AD，∴∠ADC＝∠ACD，∴∠FGD＝∠ADC.
1. 如图，AB 是 ⊙O 的直径，C 、D 是圆上的两点,∠ABD=40°,则∠BCD =＿＿＿_.
2. 如图，∠A=50°， ∠ABC=60°，BD 是 ⊙O 的直径，则 ∠AEB 等于 （ ） A. 70° B. 110° C. 90° D. 120°
3. 在 ⊙O 中，∠CBD=30°，∠BDC=20°，求∠A.
解：∵∠CBD=30°，∠BDC=20°∴∠C=180° -∠CBD -∠BDC=130°∴∠A=180° -∠C = 50°（圆内接四边形对角互补）
变式：已知 ∠OAB 等于40°，求∠C 的度数.
4. 如图，△ABC 内接于⊙O，AB=BC，∠ABC=120°，AD 为 ⊙O 的直径，AD=6，那么 AB 的值为（　　）
A. 3 B. C. D. 2
5. 如图，点 A、B、D、E 在 ⊙O 上，弦 AE、BD 的延长线相交于点 C.若 AB 是 ⊙O 的直径，D 是 BC 的中点．(1) 试判断 AB、AC 之间的大小关系，并给出证明；
解：(1)AB＝AC.证明如下：连接 AD，∵AB 是 ⊙O 的直径，∴∠ADB＝90°， 即 AD⊥BC.∵BD＝DC，∴AD 垂直平分 BC，∴AB＝AC；
(2) 在上述题设条件下，当 △ABC 为正三角形时，点E 是否为 AC 的中点？为什么？
(2)当 △ABC 为正三角形时，E 是 AC 的中点．理由如下：连接 BE，∵AB 为 ⊙O 的直径，∴∠BEA＝90°，即 BE⊥AC.∵△ABC 为正三角形，∴AE＝EC，即 E 是 AC 的中点．