
专题30 中考热点图形的旋转填空选择题专项训练-2023年中考数学二轮复习核心考点专题提优拓展训练
展开专题30 中考热点图形的旋转填空选择题专项训练(解析版)
专题诠释:几何图形的旋转是近几年中考的热点,由于旋转变换中植入了图形运动变化的因素,得到的图形与原图形之间相互依赖,就想应地提升了思维深度与思维含量,对学生动态作图,图形抽象,逻辑推理等能力要求大为提高。
一.选择题(共15小题)
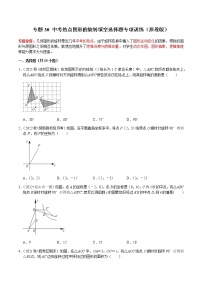
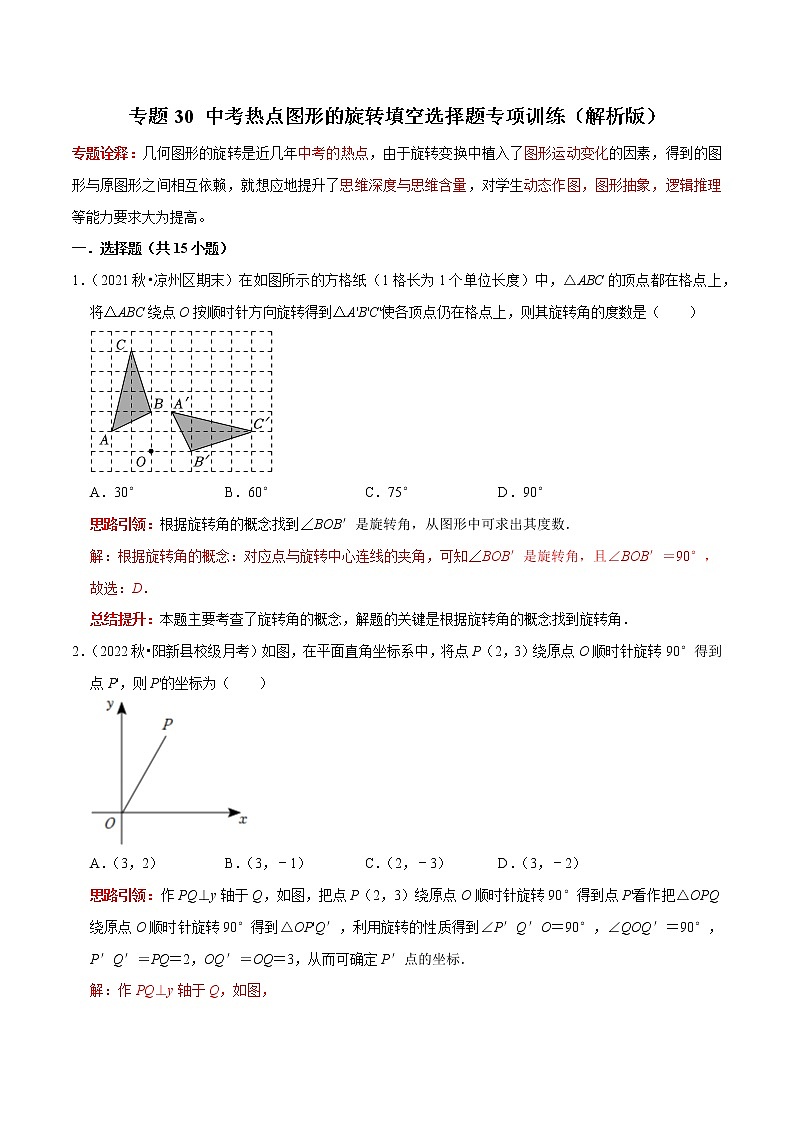
1.(2021秋•凉州区期末)在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C'使各顶点仍在格点上,则其旋转角的度数是( )
A.30° B.60° C.75° D.90°
思路引领:根据旋转角的概念找到∠BOB′是旋转角,从图形中可求出其度数.
解:根据旋转角的概念:对应点与旋转中心连线的夹角,可知∠BOB′是旋转角,且∠BOB′=90°,
故选:D.
总结提升:本题主要考查了旋转角的概念,解题的关键是根据旋转角的概念找到旋转角.
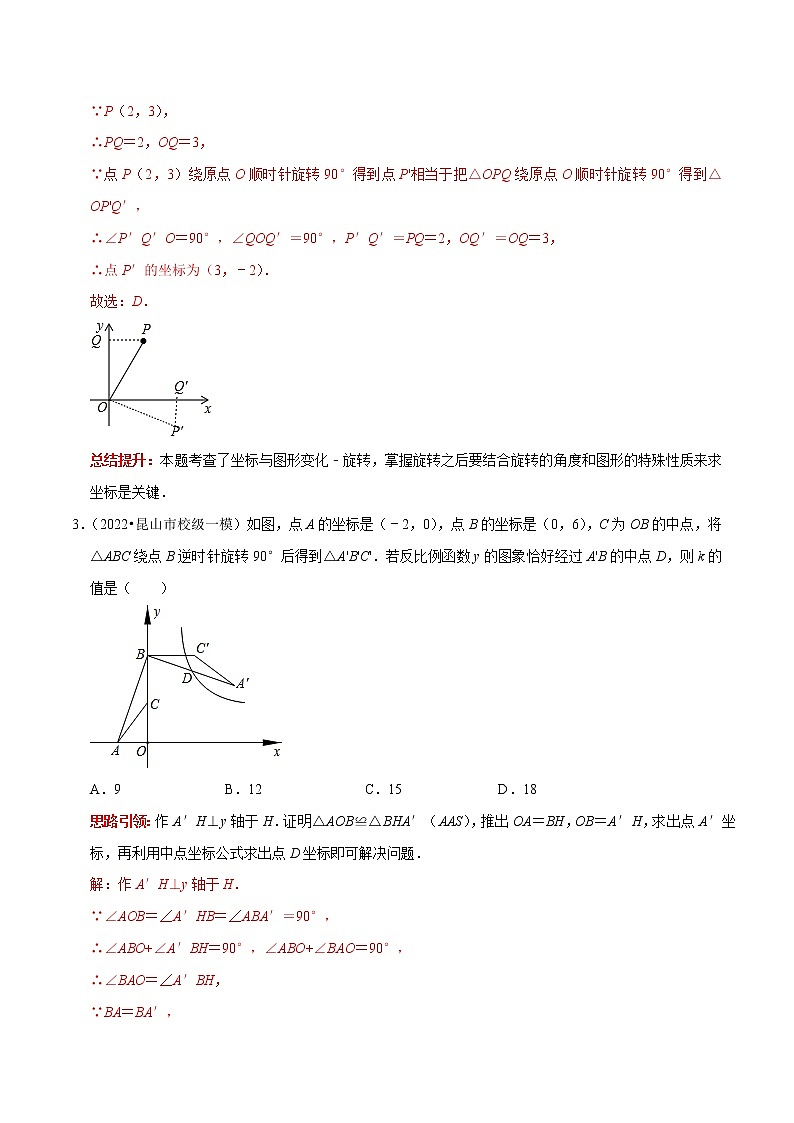
2.(2022秋•阳新县校级月考)如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为( )
A.(3,2) B.(3,﹣1) C.(2,﹣3) D.(3,﹣2)
思路引领:作PQ⊥y轴于Q,如图,把点P(2,3)绕原点O顺时针旋转90°得到点P'看作把△OPQ绕原点O顺时针旋转90°得到△OP'Q′,利用旋转的性质得到∠P′Q′O=90°,∠QOQ′=90°,P′Q′=PQ=2,OQ′=OQ=3,从而可确定P′点的坐标.
解:作PQ⊥y轴于Q,如图,
∵P(2,3),
∴PQ=2,OQ=3,
∵点P(2,3)绕原点O顺时针旋转90°得到点P'相当于把△OPQ绕原点O顺时针旋转90°得到△OP'Q′,
∴∠P′Q′O=90°,∠QOQ′=90°,P′Q′=PQ=2,OQ′=OQ=3,
∴点P′的坐标为(3,﹣2).
故选:D.
总结提升:本题考查了坐标与图形变化﹣旋转,掌握旋转之后要结合旋转的角度和图形的特殊性质来求坐标是关键.
3.(2022•昆山市校级一模)如图,点A的坐标是(﹣2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到△A'B'C'.若反比例函数y的图象恰好经过A'B的中点D,则k的值是( )
A.9 B.12 C.15 D.18
思路引领:作A′H⊥y轴于H.证明△AOB≌△BHA′(AAS),推出OA=BH,OB=A′H,求出点A′坐标,再利用中点坐标公式求出点D坐标即可解决问题.
解:作A′H⊥y轴于H.
∵∠AOB=∠A′HB=∠ABA′=90°,
∴∠ABO+∠A′BH=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠A′BH,
∵BA=BA′,
∴△AOB≌△BHA′(AAS),
∴OA=BH,OB=A′H,
∵点A的坐标是(﹣2,0),点B的坐标是(0,6),
∴OA=2,OB=6,
∴BH=OA=2,A′H=OB=6,
∴OH=4,
∴A′(6,4),
∵BD=A′D,
∴D(3,5),
∵反比例函数y=kx的图象经过点D,
∴k=15.
故选:C.
总结提升:本题考查反比例函数图象上的点的坐标特征,坐标与图形的变化﹣旋转等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
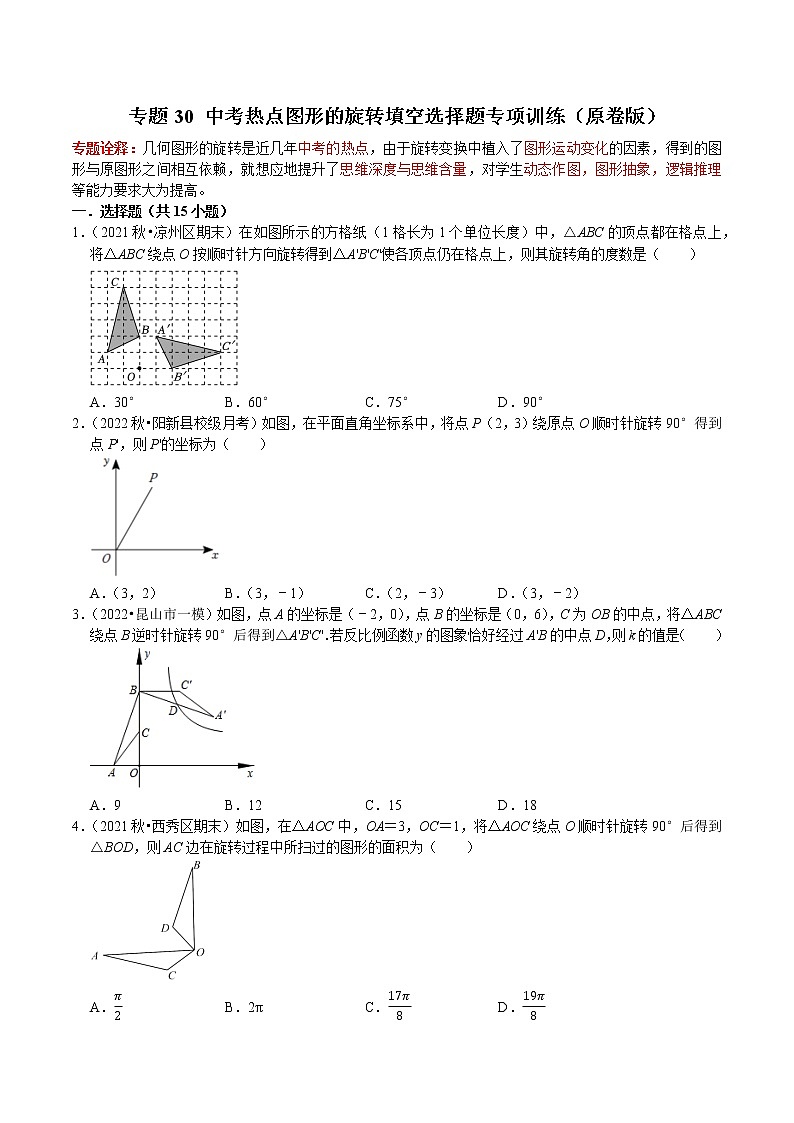
4.(2021秋•西秀区期末)如图,在△AOC中,OA=3,OC=1,将△AOC绕点O顺时针旋转90°后得到△BOD,则AC边在旋转过程中所扫过的图形的面积为( )
A.π2 B.2π C.17π8 D.19π8
思路引领:根据旋转的性质可以得到在旋转过程中所扫过的图形的面积=扇形OAB的面积﹣扇形OCD的面积,利用扇形的面积公式即可求解.
解:∵△AOC≌△BOD,
∴在旋转过程中所扫过的图形的面积=扇形OAB的面积﹣扇形OCD的面积90π×32360−90π×12360=2π,
故选:B.
总结提升:本题考查了旋转的性质以及扇形的面积公式,正确理解:阴影部分的面积=扇形OAB的面积﹣扇形OCD的面积是解题关键.
5.(2021春•成华区期末)如图,点B在第一象限,点A在x轴的正半轴上∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,则点B的对应点B′的坐标是( )
A.(−3,3) B.(﹣3,3) C.(−3,3) D.(﹣2,3)
思路引领:如图,过点B′作B′H⊥y轴于H.解直角三角形求出OH,B′H即可.
解:如图,过点B′作B′H⊥y轴于H.
在Rt△A′B′H中,∵A′B′=2,∠B′A′H=60°,
∴A′H=A′B′cos60°=1,B′H=A′B′sin60°=3,
∴OH=2+1=3,
∴B′(−3,3),
故选:A.
总结提升:本题考查坐标与图形变化﹣旋转,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
6.(2021•黄州区校级自主招生)如图,在△ABC中,∠BAC=90°,AB=AC=5cm,点D为△ABC内一点,∠BAD=15°,AD=3cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为( )cm.
A.4−6 B.5−6 C.6−6 D.7−6
思路引领:过点A作AG⊥DE于G,根据旋转的性质得∠AFG=60°,解直角三角形求出AG,进而得AF,最后根据CF=AC﹣AF得出即可.
解:过点A作AG⊥DE于G,
由旋转知,AD=AE,∠DAE=∠BAC=90°,∠CAE=∠BAD=15°,
∴∠AED=∠ADG=45°,
∴∠AFG=∠CAE+∠AED=15°+45°=60°,
∵AG⊥DE,
∴∠AGD=∠AGF=90°,
在Rt△ADG中,
∵AD=3cm,
∴AG=AD•sin∠ADG=3×22=322(cm),
在Rt△AFG中,
∵AGAF=sin∠AFG=sin60°=32,
∴AF=2AG3=2×3223=6(cm),
又∵AC=5cm,
∴CF=AC﹣AF=5−6(cm),
故选:B.
总结提升:本题主要考查旋转的性质,等腰直角三角形的性质,解直角三角形等,解题的关键是能够通过作辅助线构造特殊直角三角形,再解直角三角形来解决问题.
7.(2019秋•渠县期末)如图,正方形ABCD的边长为4,点E在CD的边上,且DE=1,△AFE与△ADE关于AE所在的直线对称,将△ADE按顺时针方向绕点A旋转90°得到△ABG,连接FG,则线段FG的长为( )
A.4 B.42 C.5 D.6
思路引领:如图,连接BE,根据轴对称的性质得到AF=AD,∠EAD=∠EAF,根据旋转的性质得到AG=AE,∠GAB=∠EAD.求得∠GAB=∠EAF,根据全等三角形的性质得到FG=BE,根据正方形的性质得到BC=CD=AB=4.根据勾股定理即可得到结论.
解:如图,连接BE,
∵△AFE与△ADE关于AE所在的直线对称,
∴AF=AD,∠EAD=∠EAF,
∵△ADE按顺时针方向绕点A旋转90°得到△ABG,
∴AG=AE,∠GAB=∠EAD.
∴∠GAB=∠EAF,
∴∠GAB+∠BAF=∠BAF+∠EAF.
∴∠GAF=∠EAB.
∴△GAF≌△EAB(SAS).
∴FG=BE,
∵四边形ABCD是正方形,
∴BC=CD=AB=4.
∵DE=1,
∴CE=3.
∴在Rt△BCE中,BE=32+42=5,
∴FG=5,
故选:C.
总结提升:本题考查了正方形的性质,勾股定理,全等三角形的判定与性质以及旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
8.(2021春•南关区期末)如图,将△ABC绕点C顺时针旋转90°得到△EDC,若点A、D、E在同一条直线上,∠ACB=25°,在∠ADC的度数是( )
A.45° B.60° C.70° D.75°
思路引领:由旋转的性质得∠DCE=∠ACB=25°,∠BCD=∠ACE=90°,AC=CE,则△ACE是等腰直角三角形,得∠CAE=∠E=45°,再由三角形的外角性质求解即可.
解:∵将△ABC绕点C顺时针旋转90°得到△EDC,
∴∠DCE=∠ACB=25°,∠BCD=∠ACE=90°,AC=CE,
∴△ACE是等腰直角三角形,
∴∠CAE=∠E=45°,
∴∠ADC=∠E+∠DCE=45°+25°=70°,
故选:C.
总结提升:此题考查了旋转的性质,等腰直角三角形的性质,三角形的外角性质等知识;熟练掌握旋转的性质,证出∠E=45°是解题的关键.
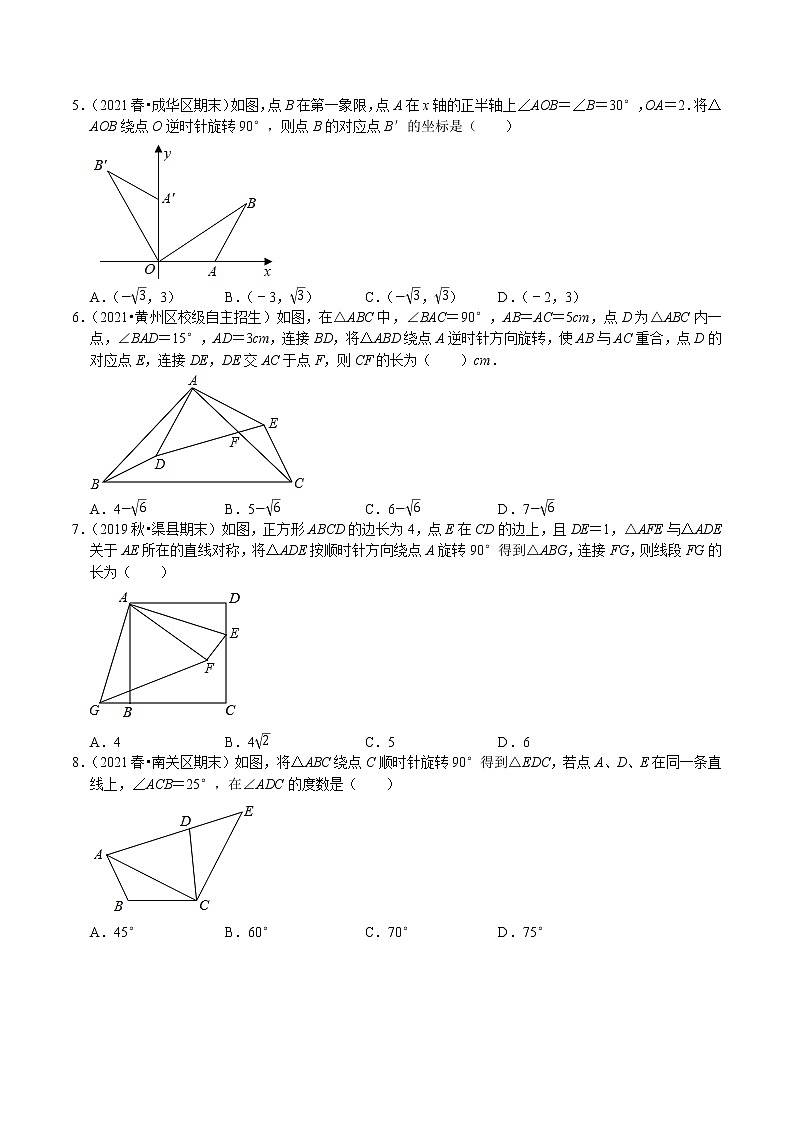
9.(内江中考)如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交y轴于点P,若△ABC与△A′B′C′关于点P成中心对称,则点A′的坐标为( )
A.(﹣4,﹣5) B.(﹣5,﹣4) C.(﹣3,﹣4) D.(﹣4,﹣3)
思路引领:先求得直线AB解析式为y=x﹣1,即可得出P(0,﹣1),再根据点A与点A'关于点P成中心对称,利用中点公式,即可得到点A′的坐标.
解:∵点B,C的坐标分别为(2,1),(6,1),∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴A(4,3),
设直线AB解析式为y=kx+b,则
3=4k+b1=2k+b,
解得k=1b=−1,
∴直线AB解析式为y=x﹣1,
令x=0,则y=﹣1,
∴P(0,﹣1),
又∵点A与点A'关于点P成中心对称,
∴点P为AA'的中点,
设A'(m,n),则m+42=0,3+n2=−1,
∴m=﹣4,n=﹣5,
∴A'(﹣4,﹣5),
故选:A.
总结提升:本题考查了中心对称,等腰直角三角形的运用,利用待定系数法得出直线AB的解析式是解题的关键.
10.(2022春•江阴市校级月考)如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,23).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为( )
A.(﹣33,23) B.(﹣23,4) C.(﹣33,6) D.(﹣23,6)
思路引领:作B1D⊥y轴于点D,则∠ODB1=∠AOD=90°,先由tan∠AOB=ABOA=33得∠AOB=30°,再由旋转得∠A1OB1=∠AOB=30°,∠OA1B1=∠OAB=90°,A1B1=AB=23,OA1=OA=6,再证明△DOB1≌△A1OB1,得DB1=A1B1=23,OD=OA1=6,则点B1的坐标为(﹣23,6).
解:如图,作B1D⊥y轴于点D,则∠ODB1=∠AOD=90°,
∵四边形OABC是矩形,
∴∠OAB=90°,
∵A(﹣6,0),C(0,23),
∴OA=6,AB=OC=23,
∴tan∠AOB=ABOA=236=33,
∴∠AOB=30°,
由旋转得∠A1OB1=∠AOB=30°,∠OA1B1=∠OAB=90°,A1B1=AB=23,OA1=OA=6,
∴∠DOB1=30°=∠A1OB1,∠ODB1=∠OA1B1,
在△DOB1和△A1OB1中,
∠ODB1=∠OA1B1∠DOB1=∠A1OB1OB1=OB1,
∴△DOB1≌△A1OB1(AAS),
∴DB1=A1B1=23,OD=OA1=6,
∴点B的对应点B1的坐标为(﹣23,6),
故选:D.
总结提升:此题重点考查矩形的性质、旋转的性质、全等三角形的判定与性质、锐角三角函数、图形与坐标等知识,求得∠AOB=30°是解题的关键.
11.(2022秋•渝中区期末)如图,在矩形ABCD中,AD=1,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则四边形ABCE的面积为( )
A.22−1 B.2 C.2−12 D.2−1
思路引领:由旋转的性质可得BC=EF=AD=1,AE=AB,可求AE的长,即可求解.
解:∵将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,
∴BC=EF=AD=1,AE=AB,
∵DE=EF=1,
∴AE=2=AB,
∴EC=2−1,
∴四边形ABCE的面积=12×(2+2−1)×1=2−12,
故选:C.
总结提升:本题考查了旋转的性质,矩形的性质,掌握旋转的性质是解题的关键.
12.(2019•梁子湖区模拟)如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于( )
A.5−12 B.5−14 C.3−52 D.3−54
思路引领:首先证明BD∥AE,可得△AEF∽△BDF,推出S△AEFS△BDF=(AEBD)2,想办法求出AEBD即可解决问题;
解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BC=BE,
∴∠C=∠BEC=72°,
∴∠EBC=36°,
∴∠ABE=∠A=36°,
∵∠DBE=72°,
∴∠ABD=∠A=36°,
∴BD∥AE,
∴△AEF∽△BDF,
∴S△AEFS△BDF=(AEBD)2,
设BC=BE=AE=x,CE=2﹣x,
∵∠C=∠C,∠CBE=∠A,
∴△CBE∽△CAB,
∴CBCA=CECB,
∴BC2=CE•CA,
∴x2=(2﹣x)2,
∴x2+2x﹣4=0,
∴x=﹣1+5,或x=﹣1−5(舍),
∴S△AEFS△BDF=(AEBD)2=3−52
故选:C.
总结提升:本题主要考查了等腰三角形的性质,以及旋转的性质,相似三角形的判定和性质,解题的关键是正确寻找相似三角形解决问题,学会利用参数解决问题,属于中考常考题型.
13.(2022秋•惠山区校级月考)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=27,AD=2,将△ABC绕点C顺时针方向旋转后得△A′B′C,当A′B′恰好经过点D时,△B′CD为等腰三角形,若BB′=2,则AA′等于( )
A.11 B.23 C.13 D.14
思路引领:过D作DE⊥BC于E,根据旋转的性质得到∠DB′C=∠ABC=90°,B′C=BC,A′C=AC,∠A′CA=∠B′CB,推出△B′CD为等腰直角三角形,根据相似三角形的性质即可得到结论.
解:过D作DE⊥BC于E,
则BE=AD=2,DE=27,
设B′C=BC=x,
则DC=2x,
∴DC2=DE2+EC2,即2x2=28+(x﹣2)2,
解得:x=4(负值舍去),
∴BC=4,AC=AB2+BC2=211,
∵将△ABC绕点C顺时针方向旋转后得△A′B′C,
∴∠DB′C=∠ABC=90°,B′C=BC,A′C=AC,∠A′CA=∠B′CB,
∴A′CB′C=ACBC
∴△A′CA∽△B′CB,
∴A′AB′B=ACBC,即A′A2=2114
∴AA′=11,
故选:A.
总结提升:本题考查了旋转的性质,等腰直角三角形的性质,相似三角形的判定和性质,勾股定理,正确的识别图形是解题的关键.
14.(2022秋•丛台区校级期末)如图,F是线段CD上除端点外的一点,将△ADF绕正方形ABCD的顶点A按顺时针方向旋转90°,得到△ABE,连接EF交AB于点H,则下列结论正确的是( )
A.∠EAF=120° B.EB:AD=EH:HF
C.AF2=EH⋅EF D.AE:EF=1:3
思路引领:由已知可得△ABE≌△ADF,从而得到∠EAB=∠DAF,AE=AF;由∠EAF=∠BAE+∠FAB=90°=∠DAF+∠FAB=90°,可知A不正确;由∠EAF=90°,AE=AF,可知△AEF是等腰直角三角形,所以EF=2AE,则D不正确;若AF2=EH•EF成立,可得EH=12EF,即H是EF的中点,而H不一定是EF的中点,故C不正确;由AB∥CD,由平行线分线段成比例可得EB:BC=EH:HF,故B正确.
解:∵△ADF绕正方形ABCD的顶点A顺时针旋转90°,得到△ABE,
∴△ABE≌△ADF,
∴∠EAB=∠DAF,
∴∠EAF=∠BAE+∠FAB=90°=∠DAF+∠FAB=90°,
故A不正确;
∵∠EAF=90°,AE=AF,
∴△AEF是等腰直角三角形,
∴EF=2AE,
∴AE:EF=1:2,
故D不正确;
若AF2=EH•EF成立,
∵AE:EF=1:2,
∴EH=22AF,
∴EH=12EF,
即H是EF的中点,H不一定是EF的中点,
故C不正确;
∵AB∥CD,
∴EB:BC=EH:HF,
∵BC=AD,
∴EB:AD=EH:HF,
故B正确;
故选:B.
总结提升:本题考查正方形的性质,三角形的旋转;抓住三角形旋转的本质,旋转前后的三角形全等,得到△AEF是等腰直角三角形是解本题的关键.
15.(2022•金华模拟)如图,四边形ABCD是边长为2的菱形,且有一个内角为72°,现将其绕点D顺时针旋转得到菱形A′B′C′D,线段AB与线段B'C'交于点P,连接BB′.当五边形A′B′BCD为正五边形时,BPAP长为( )
A.1 B.5+12 C.5−1 D.5−12
思路引领:连接BC′,AC′,根据正五边形的内角和先求出∠CDA′=108°,再根据菱形和旋转的性质可得CD=AD=DC′=AB=2,AB∥CD,A′D∥B′C′,∠ADC=∠A′DC′=72°,∠CDC′=∠ADA′,从而可得∠CDC′=∠ADC′=36°,进而可得点D,C′,B在同一条直线上,然后求出∠ABC′=∠BAC′=36°,从而可设AC′=BC′=x,再证明△BAC′∽△BDA,利用相似三角形的性质求出BC′的长,最后再证明△BPC′是等腰三角形,从而可得BC′=BP=5−1,进而求出AP的长,进行计算即可解答.
解:连接BC′,AC′,
∵五边形A'B'BCD为正五边形,
∴∠CDA′=(5−2)×180°5=108°,
∵菱形ABCD绕点D顺时针旋转得到菱形A'B'C'D,
∴CD=AD=DC′=AB=2,AB∥CD,A′D∥B′C′,∠ADC=∠A′DC′=72°,∠CDC′=∠ADA′,
∴∠CDC′=∠ADA′=∠CDA′﹣∠ADC=36°,
∴∠ADC′=∠ADC﹣∠CDC′=36°,
∴∠CDC′=∠ADC′=36°,
∴DC′平分∠ADC,
∴点D,C′,B在同一条直线上,
∵AD=AB,
∴∠ADB=∠ABD=36°,
∵AD=DC′,
∴∠DAC′=∠DC′A=72°,
∵AB∥CD,
∴∠DAB=180°﹣∠ADC=108°,
∴∠BAC′=∠DAB﹣∠DAC′=36°,
∴∠ABC′=∠BAC′=36°,
∴AC′=BC′,
设AC′=BC′=x,
∵∠ABC′=∠ABD,∠BAC′=∠ADB=36°,
∴△BAC′∽△BDA,
∴BABD=BC′BA,
∴2x+2=x2,
∴x=5−1或x=−5−1(舍去),
∴AC′=BC′=5−1,
∵A′D∥B′C′,
∴∠A′DC′=∠BC′B′=72°,
∴∠BPC′=180°﹣∠BC′P﹣∠ABD=72°,
∴∠BC′P=∠BPC′=72°,
∴BC′=BP=5−1,
∴AP=AB﹣BP=3−5,
∴BPAP=5−13−5=5+12,
故选:B.
总结提升:本题考查了相似三角形的判定与性质,菱形的性质,旋转的性质,正多边形和圆,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
二.填空题(共10小题)
16.(2012•南昌)如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .
思路引领:利用正方形的性质和等边三角形的性质证明△ABE≌△ADF(SSS),由全等三角形的性质和已知条件即可求出当BE=DF时,∠BAE的大小,应该注意的是,正三角形AEF可以在正方形的内部也可以在正方形的外部,所以要分两种情况分别求解.
解:①当正三角形AEF在正方形ABCD的内部时,如图1,
∵正方形ABCD与正三角形AEF的顶点A重合,
当BE=DF时,
∴AB=ADBE=DFAE=AF,
∴△ABE≌△ADF(SSS),
∴∠BAE=∠FAD,
∵∠EAF=60°,
∴∠BAE+∠FAD=30°,
∴∠BAE=∠FAD=15°,
②当正三角形AEF在正方形ABCD的外部时.
∵正方形ABCD与正三角形AEF的顶点A重合,
当BE=DF时,
∴AB=ADBE=DFAE=AF,
∴△ABE≌△ADF(SSS),
∴∠BAE=∠FAD,
∵∠EAF=60°,
∴∠BAE=(360°﹣90°﹣60°)×12+60°=165°,
∴∠BAE=∠FAD=165°
故答案为:15°或165°.
总结提升:本题考查了正方形的性质、等边三角形的性质、旋转的性质以及全等三角形的判定和全等三角形的性质和分类讨论的数学思想,题目的综合性不小.
17.(2019春•江宁区校级月考)如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是 .
思路引领:先根据BE=DF,AE=AF,AB=AD判定△ABE≌△ADF,再根据∠BAE的位置求得其度数.
解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵△AEF是等边三角形,
∴AE=AF,∠EAF=60°,
分两种情况:
①如图1,当正△AEF在正方形ABCD内部时,
在△ABE和△ADF中,BE=DFAE=AFAB=AD,
∴△ABE≌△ADF(SSS),
∴∠BAE=∠DAF=12(90°﹣60°)=15°;
②如图2,当正△AEF在正方形ABCD外部时,
在△ABE和△ADF中,BE=DFAE=AFAB=AD
∴△ABE≌△ADF(SSS),
∴∠BAE=∠DAF=12(360°﹣90°+60°)=165°;
故答案为:15°或165°.
总结提升:本题主要考查了正方形和等边三角形的性质,解决问题的关键是掌握全等三角形的判定与性质.在求∠BAE的度数时,需要分两种情况进行讨论.
18.(2021秋•潮安区期中)如图,在等边△ABC中,AB=12,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 .
思路引领:由等边三角形的性质得出BC=AB=12,求出BD,由旋转的性质得出△ACE≌△ABD,得出CE=BD,即可得出结果.
解:∵△ABC是等边三角形,
∴BC=AB=12,
∵BC=3BD,
∴BD=13BC=4,
由旋转的性质得:△ACE≌△ABD,
∴CE=BD=4.
故答案为:4.
总结提升:本题考查了旋转的性质、等边三角形的性质、全等三角形的性质;熟练掌握旋转的性质和等边三角形的性质是解决问题的关键.
19.(2018•衡阳)如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按顺时针方向旋转而得到的,则旋转的角度为 .
思路引领:由△COD是由△AOB绕点O按顺时针方向旋转而得到,再结合已知图形可知旋转的角度是∠BOD的大小,然后由图形即可求得答案.
解:∵△COD是由△AOB绕点O按顺时针方向旋转而得,
∴OB=OD,
∴旋转的角度是∠BOD的大小,
∵∠BOD=90°,
∴旋转的角度为90°.
故答案为:90°.
总结提升:此题考查了旋转的性质.解此题的关键是理解△COD是由△AOB绕点O按顺时针方向旋转而得的含义,找到旋转角.
20.(2021•费县二模)如图,将△ABC绕点A顺时针旋转角100°,得到△ADE,若点E恰好在CB的延长线上,则∠BED等于 度.
思路引领:证明∠ABE+∠ADE=180°,推出∠BAD+∠BED=180°即可解决问题.
解:∵∠ABC=∠ADE,∠ABC+∠ABE=180°,
∴∠ABE+∠ADE=180°,
∴∠BAD+∠BED=180°,
∵将△ABC绕点A顺时针旋转角100°,得到△ADE,
∴∠BAD=100°,
∴∠BED=180°﹣100°=80°.
故答案为:80.
总结提升:本题考查旋转的性质,解题的关键是理解题意,灵活运用所学知识解决问题.
21.(2022春•市北区期中)如图,在△ABC中,∠ACB=90°,∠ABC=30°,AC=2cm.现在将△ABC绕点C逆时针旋转至△A′B′C′,使得点A′恰好落在AB上,连接BB′,则△CBB′的面积为 33 cm2.
思路引领:由题意可得△AA'C是等边三角形,可得旋转角为60°,可得△BCB'是等边三角形,即可求解.
解:∵∠ACB=90°,∠ABC=30°,AC=2cm,
∴∠A=60°,AB=4cm,BC=23cm,
∵△ABC绕点C逆时针旋转至△A′B′C′,
∴A'C=60°,A'B'=4cm,BC=B'C,∠ACA'=∠BCB',
∵AC=A'C,∠A=60°,
∴△ACA'是等边三角形,
∴∠ACA'=60°,
∴∠BCB'=60°,
∴△BCB'是等边三角形,
∴△CBB′的面积=34×(23)2=33cm2,
故答案为:33.
总结提升:本题考查了旋转的性质,等边三角形的性质,勾股定理,关键是证△CB'B是等边三角形.
22.(2022春•雁塔区校级期中)如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为 .
思路引领:由旋转的性质可得∠C=∠C',AB=AB',由等腰三角形的性质可得∠C=∠CAB',∠B=∠AB'B,由三角形的外角性质和三角形内角和定理可求解.
解:∵AB'=CB',
∴∠C=∠CAB',
∴∠AB'B=∠C+∠CAB'=2∠C,
∵将△ABC绕点A按逆时针方向旋转得到△AB'C',
∴∠C=∠C',AB=AB',
∴∠B=∠AB'B=2∠C,
∵∠B+∠C+∠CAB=180°,
∴3∠C=180°﹣108°,
∴∠C=24°,
∴∠C'=∠C=24°,
故答案为:24°.
总结提升:本题考查了旋转的性质,等腰三角形的性质,灵活运用这些的性质解决问题是本题的关键.
23.(2022秋•温岭市期末)如图,把双曲线y=kx(k>0,x>0)绕着原点逆时针旋转45°与y轴交于点B,
(1)若点B(0,2),则k= ;
(2)若点A(3,5)在旋转后的曲线上,则k= .
思路引领:(1)设B的对应点为B',过B'作B'M⊥y轴于M,由∠BOB'=45°,知△B'OM是等腰直角三角形,可得B'(2,2),故k=2×2=2;
(2)将A顺时针旋转45°得A',则双曲线y=kx过A',过A作AG⊥OA,交OA'延长线于G,过A作AE⊥y轴,过G作GK⊥x轴于K,交AE于F,过A'作A'H⊥x轴于H,证明△OAE≌△AGF(AAS),可得OE=AF=5,AE=FG=3,从而EF=AE+AF=8=OK,GK=FK﹣FG=OE﹣FG=2,由△OA'H∽△OGK,有34217=OH8=A′H2,即得OH=42,A'H=2,故A'(42,2),k=42×2=8.
解:(1)设B的对应点为B',过B'作B'M⊥y轴于M,如图:
∵B(0,2),
∴OB=2=OB',
∵∠BOB'=45°,
∴△B'OM是等腰直角三角形,
∴OM=B'M=OB′2=2,
∴B'(2,2),
∴k=2×2=2,
故答案为:2;
(2)将A顺时针旋转45°得A',则双曲线y=kx过A',过A作AG⊥OA,交OA'延长线于G,过A作AE⊥y轴,过G作GK⊥x轴于K,交AE于F,过A'作A'H⊥x轴于H,如图:
∵∠AOA'=45°,AG⊥OA,
∴∠OAG=90°,OA=AG,
∴∠OAE=90°﹣∠FAG=∠AGF,
∵∠OEA=∠AFG=90°,
∴△OAE≌△AGF(AAS),
∴OE=AF=5,AE=FG=3,
∴EF=AE+AF=3+5=8=OK,GK=FK﹣FG=OE﹣FG=5﹣3=2,
∴OG=OK2+GK2=82+22=217,
∵GK⊥x轴,A'H⊥x轴,
∴A'H∥GK,
∴△OA'H∽△OGK,
∴OA′OG=OHOK=A′HGK,
∵OA'=OA=32+52=34,
∴34217=OH8=A′H2,
∴OH=42,A'H=2,
∴A'(42,2),
∴k=42×2=8,
故答案为:8.
总结提升:本题考查反比例函数的应用,涉及旋转变换,解题的关键是求出A,B的对应点坐标.
24.(2022秋•金水区校级期末)如图,已知直角三角形ABO中,AO=3,将△ABO绕点O点旋转至△A'B'O的位置,且A'在OB的中点,B'在反比例函数y=kx上,则k的值为 .
思路引领:连接AA′,作B′E⊥x轴于点E,根据直角三角形斜边中线的性质和旋转的性质得出△AOA′是等边三角形,从而得出∠AOB=∠A′OB′=60°,即可得出∠B′OE=60°,解直角三角形求得B′的坐标,进一步求得k=3.
解:连接AA′,作B′E⊥x轴于点E,
由题意知OA=OA′,A'是OB中点,∠AOB=∠A′OB′,OB′=OB,
∴AA′=12OB=OA′,
∴△AOA′是等边三角形,
∴∠AOB=60°,
∴OB=2OA=23,∠B′OE=60°,
∴OB′=23,
∴OE=12OB′=3,
∴B′E=3OE=3,
∴B′(1,3),
∵B'在反比例函数y=kx上,
∴k=1×3=3.
故答案为:3.
总结提升:本题考查反比例函数图象上点的坐标特征,坐标与图形变化﹣性质,解答本题的关键是明确题意,利用数形结合的思想解答.
25.(2021春•江阴市期中)如图,在平面直角坐标系中,点A(a,4)为第一象限内一点,且a<4.连接OA,并以点A为旋转中心,把OA逆时针旋转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则a的值等于 .
思路引领:过A作AE⊥x轴,过B作BD⊥AE,利用同角的余角相等得到一对角相等,再由一对直角相等,且AO=AB,利用AAS得出三角形AOE与三角形ABD全等,由确定三角形的对应边相等得到AE=BD=4,OE=AD=a,进而表示出ED及OE+BD的长,即可表示出B坐标;由A与B都在反比例图象上,得到A与B横纵坐标乘积相等,列出关系式,于是得到结论.
解:过A作AE⊥x轴,过B作BD⊥AE,
∵∠OAB=90°,
∴∠OAE+∠BAD=90°,
∵∠AOE+∠OAE=90°,
∴∠BAD=∠AOE,
在△AOE和△BAD中,
∠AOE=∠BAD∠AEO=∠BDA=90°AO=BA,
∴△AOE≌△BAD(AAS),
∴AE=BD=4,OE=AD=a,
∴DE=4﹣a,OE+BD=a+4,
则B(a+4,4﹣a);
∵A与B都在反比例图象上,得到4a=(4+a)(4﹣a),
解得:a=﹣2+25(负值舍去),
故答案为:﹣2+25.
总结提升:此题属于反比例函数综合题,涉及的知识有:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形的性质,以及一元二次方程的解法,熟练掌握反比例函数的性质是解本题的关键.
专题30 中考热点图形的旋转填空选择题专项训练-2023年中考数学二轮复习核心考点拓展训练(原卷版): 这是一份专题30 中考热点图形的旋转填空选择题专项训练-2023年中考数学二轮复习核心考点拓展训练(原卷版),共6页。试卷主要包含了cm等内容,欢迎下载使用。
专题32 中考热点规律探究填空选择专项训练-2023年中考数学二轮复习核心考点专题提优拓展训练: 这是一份专题32 中考热点规律探究填空选择专项训练-2023年中考数学二轮复习核心考点专题提优拓展训练,文件包含专题32中考热点规律探究填空选择专项训练解析版docx、专题32中考热点规律探究填空选择专项训练原卷版docx等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。
专题31 中考热点新定义问题专项训练-2023年中考数学二轮复习核心考点专题提优拓展训练: 这是一份专题31 中考热点新定义问题专项训练-2023年中考数学二轮复习核心考点专题提优拓展训练,文件包含专题31中考热点新定义问题专项训练解析版docx、专题31中考热点新定义问题专项训练原卷版docx等2份试卷配套教学资源,其中试卷共62页, 欢迎下载使用。