23.3图形的变换 课件

这是一份23.3图形的变换 课件

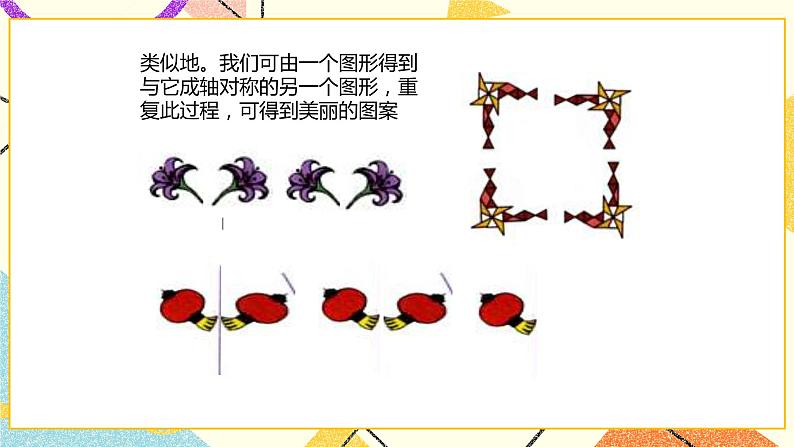
23章 图形的变换23.3 轴对称变换23.3轴对称变换动手试一试在一 张半透明的纸的左边画一只左脚印，在把这张纸对折后描图，打开对折的纸。就能得到相应的动脑想一 想左脚印和右脚印有什么关系？成轴对称对称轴是折痕所在的 直线，既直线︱右脚印类似地。我们可由一个图形得到与它成轴对称的另一个图形，重复此过程，可得到美丽的图案①对称轴方向和位置发生变化时，得到的图形的方向和位置也 会发生变化②由一个平面图形可以得到它关于一条直线L对称的图形，这个图形与原图形的形状、大小完全一样；③新图形上的每一点，都是原图形上的某一点关于直线L的对称点；④连接任意一 对对于的对应点的线段被对称轴垂直平分。小结：轴对称变换由一个平面图形得到它的轴对称图形叫做轴对称变换成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到。一个轴对称图形也可以看作以它的一部分为基础，经轴对称变换扩展而得到探究一如果有一 个图形和一条直线，如何作出与这个图形关于这条直线对称的图形呢？例1、 如图，已知△ABC和直线L，作△ABC 关于直线L对称的图形归纳几何图形都可以看作由点组成，只要作出这些点关于对称轴的对应点，再连接对应点，就可以得到原图形的轴对称图形对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点，再连接对应点，就可以得到原图形的轴对称图形请你用所学的知识来欣赏下列美丽的图案要在燃气管道L上修建一个泵站，分别向A、B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？你可以在L上找几个点试一试，能发现什么规律吗？哈，我知道怎样作ABC下面的第二个时间可由第一个怎样变换而得到BYE BYE