2023春长沙四大名校集团八年级同步复习——专题01 斜边中线定理无答案

专题01 斜边中线定理

一、基础知识

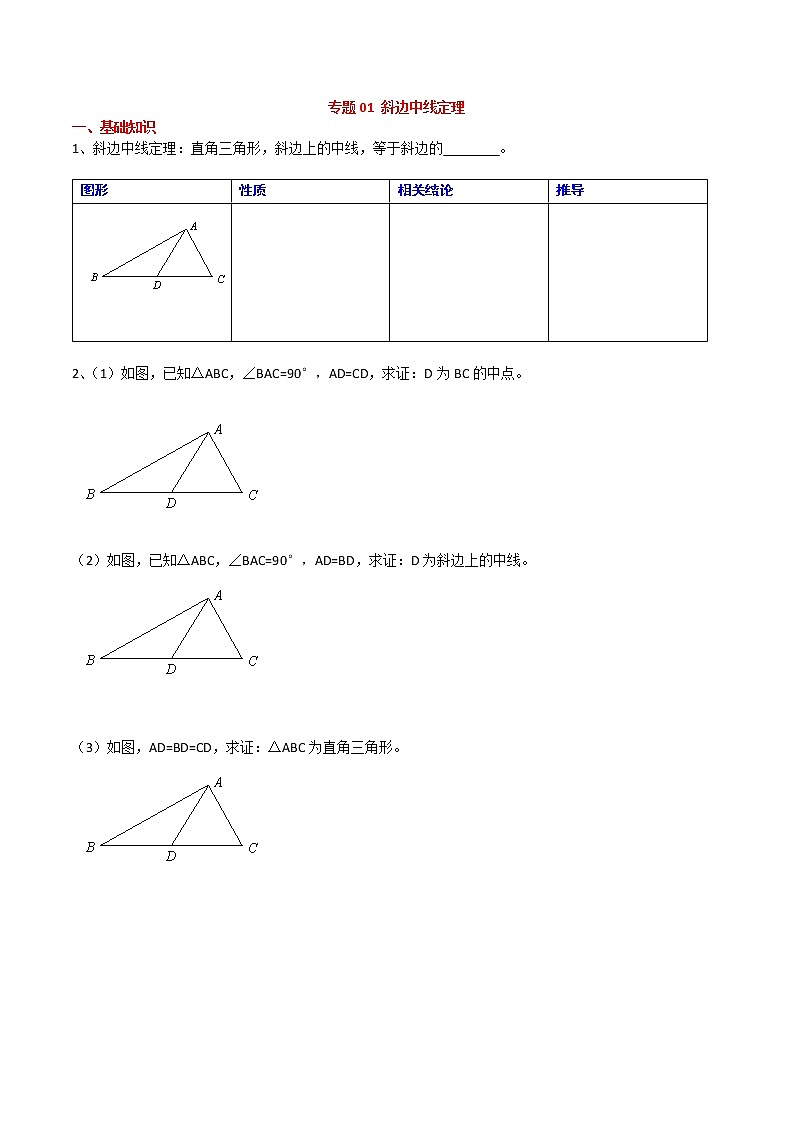
1、斜边中线定理：直角三角形，斜边上的中线，等于斜边的        。

2、（1）如图，已知△ABC，∠BAC=90°，AD=CD，求证：D为BC的中点。

（2）如图，已知△ABC，∠BAC=90°，AD=BD，求证：D为斜边上的中线。

（3）如图，AD=BD=CD，求证：△ABC为直角三角形。

二、典题精讲

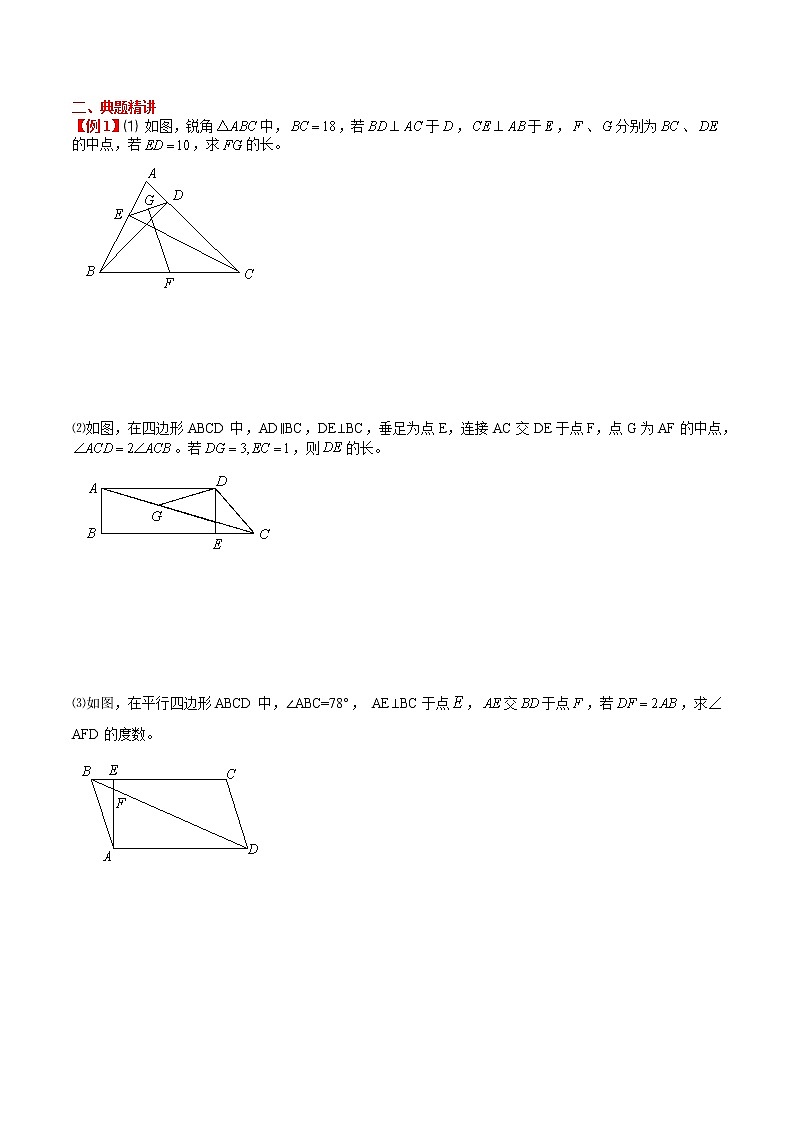
【例1】⑴ 如图，锐角中，，若于，于，、分别为、的中点，若，求的长。

⑵如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，。若，则的长。

⑶如图，在平行四边形ABCD中，∠ABC=78°， AE⊥BC于点，交于点，若，求∠AFD的度数。

【例2】已知：在中，，点在直线上，与直线垂直，垂足为，且点为中点，连接、．

（1）如图1，若点在线段上，探究线段与及与所满足的数量关系，并直接写出你得到的结论；

（2）如图2，若点在延长线上，你⑴中的结论是否发生变化？写出你的猜想并证明；

【例3】如图2，在△ABC中，∠B=2∠C，AD⊥BC于点D，点M为BC的中点，AB=10cm，求MD的长。

【例4】如图1，在△ABC中，点P为BC边的中点，直线a绕顶点A旋转，若点B，P在直线a的异侧，BM⊥直线a于点M，CN⊥直线a于点N，连接PM，PN．

⑴延长MP交CN于点E(如图2)．

①求证：△BPM≌△CPE；②求证：PM＝PN．

⑵若直线a绕点A旋转到如图3的位置时，点B，P在直线a的同侧，其他条件不变，此时PM＝PN还成立吗？若成立，请证明；若不成立，请说明理由．

⑶若直线a绕点A旋转到与BC边平行的位置时，其他条件不变．请直接判断四边形MBCN的形状及此时PM＝PN是否成立．不必说明理由．                     

【巩固练习】

1、如图，已知直角△ABC，D为斜边AB上一点，。求证：。【提示：斜边中线定理，寻找斜边】

2、如图，在正方形中，、分别是、的中点，求证：（1）；

（2）。

3、已知：△ABD和△ACE都是直角三角形，且∠ABD＝∠ACE＝90°．如图1，连接DE，设M为DE的中点．⑴求证：MB＝MC；

⑵设∠BAD＝∠CAE，固定△ABD，让Rt△ACE绕顶点A在平面内旋转到图2的位置，试问：MB＝MC是否还成立?请说明理由．