14.3《等腰三角形》课件+教案

这是一份14.3《等腰三角形》课件，文件包含143《等腰三角形》教案doc、143《等腰三角形》课件ppt等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。
14.3等腰三角形
等腰三角形的性质
共同特点
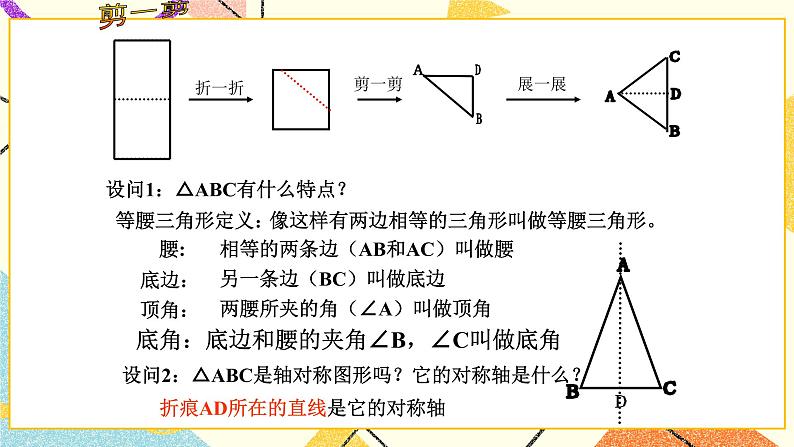
设问1：△ABC有什么特点？
等腰三角形定义：
像这样有两边相等的三角形叫做等腰三角形。
相等的两条边（AB和AC）叫做腰
另一条边（BC）叫做底边
两腰所夹的角（∠A）叫做顶角
剪一剪
设问2：△ABC是轴对称图形吗？它的对称轴是什么？
折痕AD所在的直线是它的对称轴
底角：底边和腰的夹角∠B，∠C叫做底角
设问3：你发现了什么现象，
猜一猜
猜想等腰△ABC有哪些性质？
→ 两个底角相等 → AD为底边BC上的中线 → AD为顶角∠BAC的平分线 → AD为底边BC上的高
① ∠B = ∠C② BD = CD③ ∠BAD=∠CDA④∠ADC= ∠ADB=900
等腰三角形性质性质1 等腰三角形的两个底角相等（简写成“等边对等角”）；性质2 等腰三角形的顶角平分线、底边上的中线、底边上的高 互相重合。（可简记为“三线合一”）
数学式
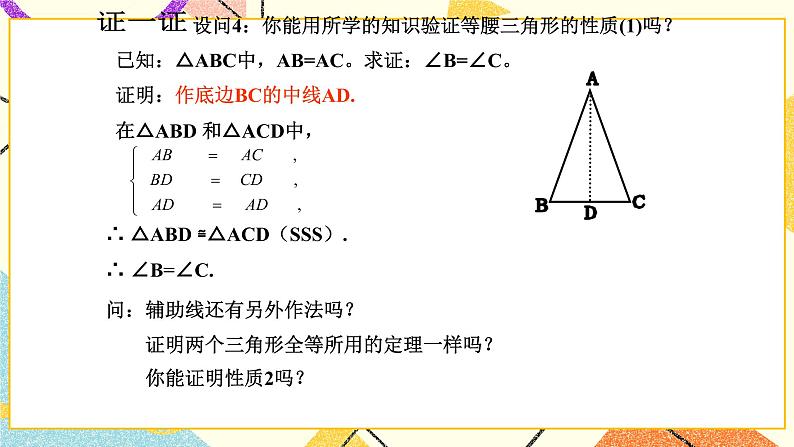
设问4：你能用所学的知识验证等腰三角形的性质(1)吗？
已知：△ABC中，AB=AC。求证：∠B=∠C。
证明：作底边BC的中线AD.在△ABD 和△ACD中，
证一证
∴ △ABD ≌△ACD（SSS）.∴ ∠B=∠C.
你能证明性质2吗？
问：辅助线还有另外作法吗？
证明两个三角形全等所用的定理一样吗？
用一用
练习1(回答) （1）已知等腰三角形的一个底角是700， 则其余两角为_______________.（2）已知等腰三角形的一个角是700， 则其余两角为___________________.（3）已知等腰三角形的一个角是1100， 则其余两角为____________________.
① 顶角+2×底角=1800
④0°＜顶角＜180°⑤0°＜底角＜90°
结论：你发现等腰三角形中顶角与底角间有什么关系？
70°,40°或55°,55°
35 °，35 °
选择题：
1、等腰三角形一腰上的高与底边所夹的角等于（ ）
A、顶角
D、底角的一半
c、顶角的2倍
B、顶角的一半
B
选择题：
2、一腰上的高与另一腰的夹角为45°，那么这个等腰三角形的底角为（ ）
A、67°50′
D、以上都不对
C、67.5°
B、135°
C
选择题：
3.已知在等腰三角形ABC中，AB的长是AC的2倍，其周长为40，则AB长为（ ）
A、20
D、25或16
C、10
B、16
B
选择题：
4.已知：△ABC中，AB=AC，BD=CF，BE=CD，∠A=50，则∠EDF等于（ ）
A、50°
D、65°
C、60°
B、55°
A
C
B
D
F
E
D
例1、在△ABC中，AB=AC，点D在AC上，且 BD=BC=AD。（1）图中共有几个等腰三角形？分别写出它们的 顶角和底角。（2）你能求出各角的度数吗？
已知:△ABC中,AB=AC,AD=BD=BC.求： △ABC各角的度数。
解：∵ AB=AC,AD=BD=BC
∴∠ABC=∠C=∠BDC
∠A=∠ABD（等边对等角）
设∠A=x则
∠BDC=∠A+∠ABD=2 x
∵∠ABC=∠C=∠BDC =2 x
∴ x+2 x+2 x=180°
∴ x=36°
∴ ∠A =36°， ∠ABC=∠C= 72°
变式1
A
B
C
D
已知:△ABC中,AB=AC, AD=ED=EC.CD=BC求△ABC各角的度数。
E
变式2
A
B
C
D
已知:如图，AB=BC=CD=ED=EF.
E
F
M
N
∠A=15°，你能求出哪些角的度数？
已知:点D、E在△ABC中, AB=AC,AD=AE. 求证：BD=CE。
A
B
C
D
E
例2
小结
等腰三角形的性质：
边：
等腰三角形两腰相等。
角：
等腰三角形两底角相等。
线段：
三线合一