初中数学24.5 三角形的内切圆精品课件ppt

导入新课

提问

      小明在一家木料厂上班，工作之余想对厂里的三角形废料进行加工：裁下一块圆形用料，怎样才能使裁下的圆的面积尽可能大呢？

学生思考问题

引发学生思考，激发学生的学习兴趣

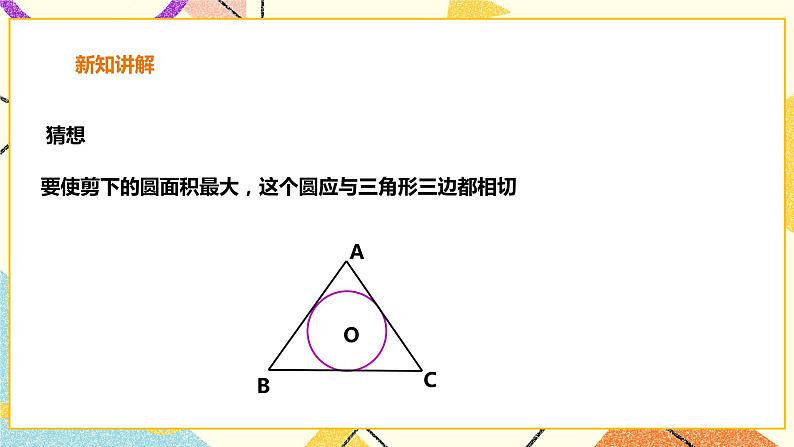
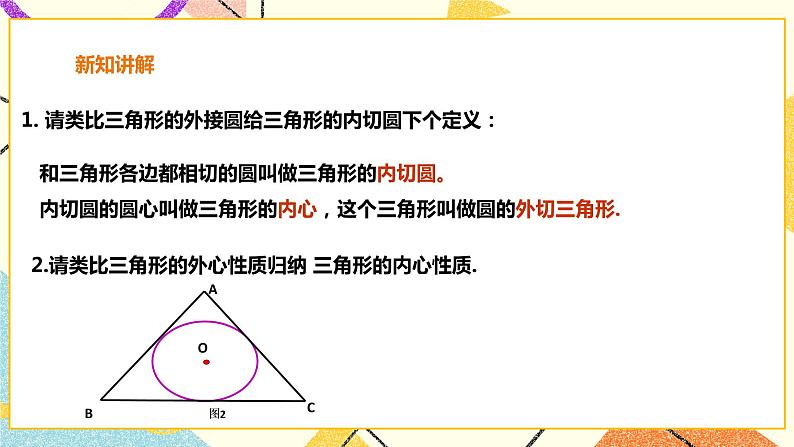
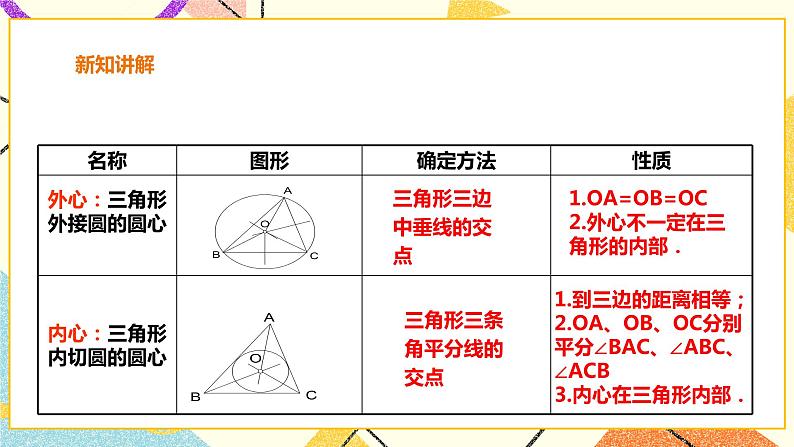
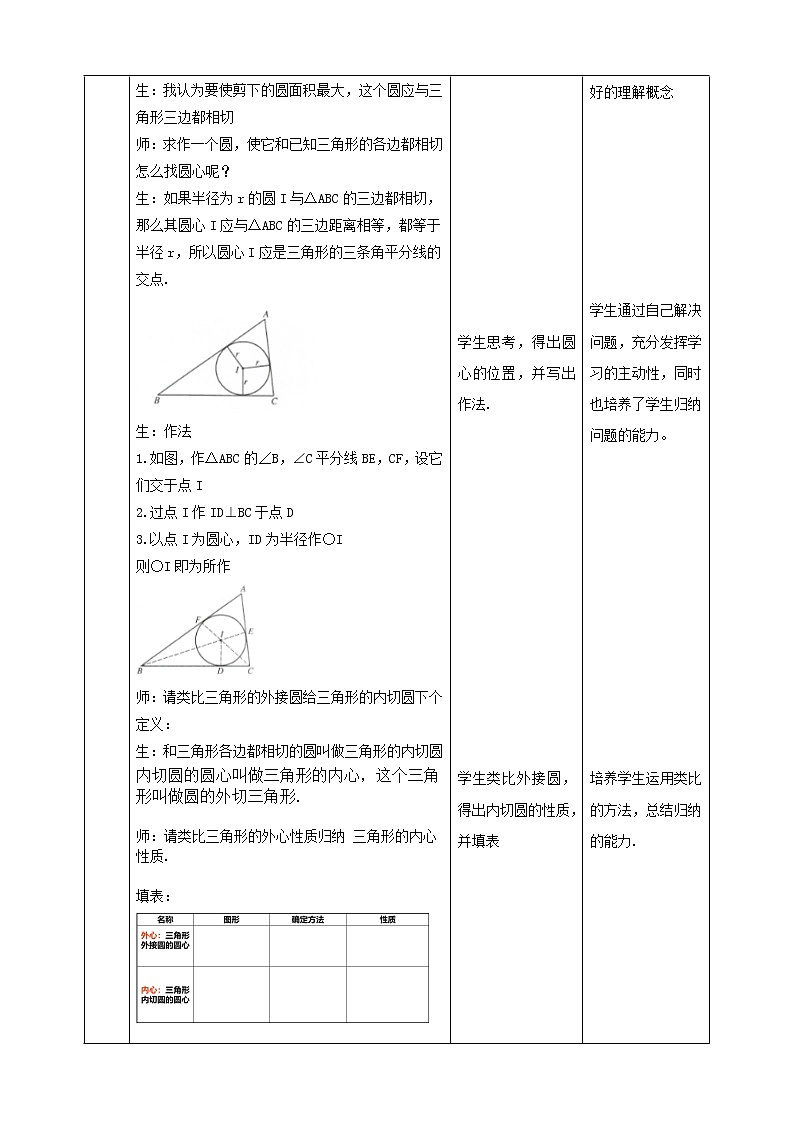
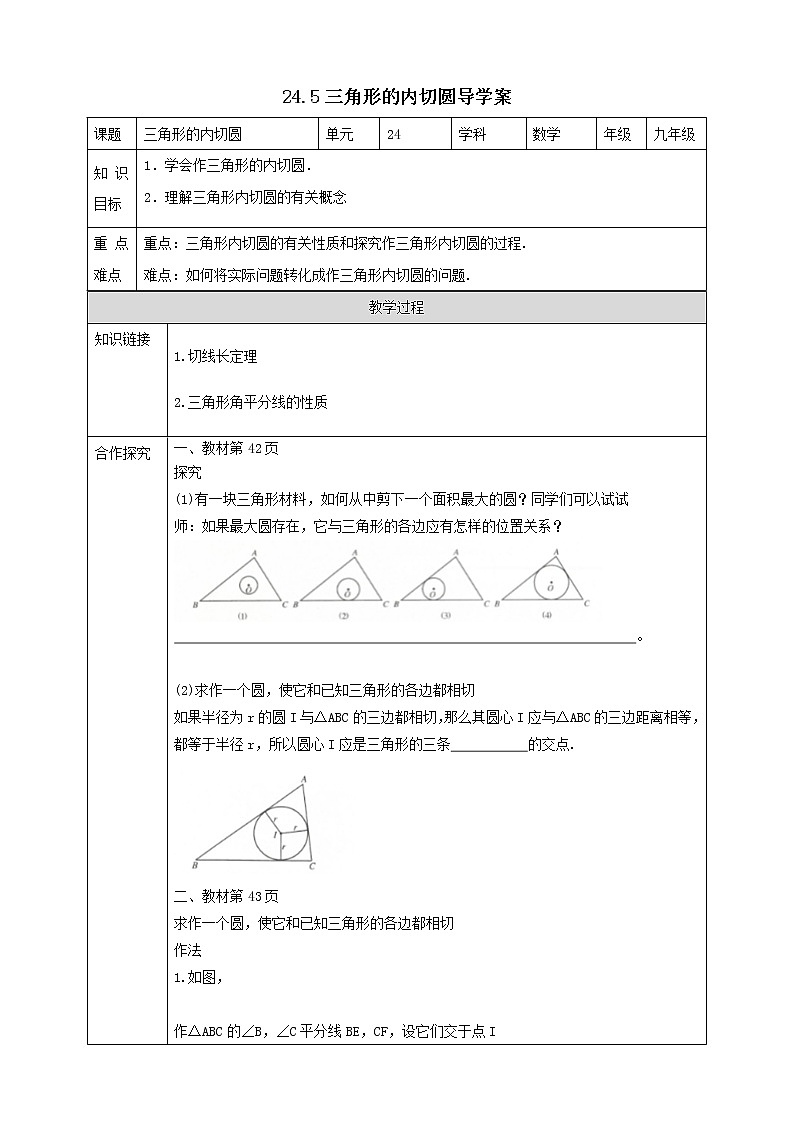
讲授新课

师：有一块三角形材料，如何从中剪下一个面积最大的圆？同学们可以试试

师：如果最大圆存在，它与三角形的各边应有怎样的位置关系？

生：我认为要使剪下的圆面积最大，这个圆应与三角形三边都相切

师：求作一个圆，使它和已知三角形的各边都相切

怎么找圆心呢？

生：如果半径为r的圆I与△ABC的三边都相切，那么其圆心I应与△ABC的三边距离相等，都等于半径r，所以圆心I应是三角形的三条角平分线的交点.

生：作法

1.如图，作△ABC的∠B，∠C平分线BE，CF，设它们交于点I

2.过点I作ID⊥BC于点D

3.以点I为圆心，ID为半径作○I

则○I即为所作

师：请类比三角形的外接圆给三角形的内切圆下个定义：

生：和三角形各边都相切的圆叫做三角形的内切圆

内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形.

师：请类比三角形的外心性质归纳 三角形的内心性质.

填表：

课件展示：

例 如图，在△ABC中，∠B=43°，∠C=61°，点I是△ABC的内心，求∠BIC的度数.

学生结合问题，试着作出最大的圆，并总结特点

学生思考，得出圆心的位置，并写出作法.

学生类比外接圆，得出内切圆的性质，并填表

学生动手练习，教师及时展示学生练习结果，并及时给予点评.

通过学生自己动手找出最大圆，能更好的理解概念

学生通过自己解决问题，充分发挥学习的主动性，同时也培养了学生归纳问题的能力。

培养学生运用类比的方法，总结归纳的能力.

通过例题讲解，让学生加深对新知识的理解，培养学生分析问题和解决问题的能力.

课堂练习

1. 已知P是三角形的两条角平分线的交点,则这个点(　　)

A.是这个三角形的外心  

B.是这个三角形的内心

C.到各边中点距离相等  

D.与顶点的连线垂直于该顶点的对边

答案：B

2.如图,等边三角形的内切圆半径为1,那么这个等边三角形的边长为(　　)

A.2        B.3       C.         D.

答案：D

3.如图,已知△ABC的内切圆☉O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD的度数

是　　.

答案：70°

4.如图,点O是△ABC的内心,过点O作EF∥BC,与AB,AC分别交于点E,F,则线段EF,BE,CF三者间的数量关系是　　　　　　　. 

答案：EF=BE+CF

5.如图，△ABC中，O是内心，∠A的平分线和△ABC的外接圆相交于点D.

求证：DO＝DB

 答案：

证明：连接BO，

     ∵  AD是∠BAC的平分线

     ∴  ∠1=∠2，

 同理   ∠3=∠4，

   而 ∠BOD=∠1+∠3，

       ∠ OBD=∠4+∠5，

  又∵∠2=∠5，

      ∴∠BOD=∠OBD.

      ∴DO=DB.

拓展提升

如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆☉O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G,连接AI.

(1)求证:DG∥CA;

(2)求证:AD=ID;

(3)若DE=4,BE=5,求BI的长.

答案：

(1)证明:如图所示,

∵点I是△ABC的内心,

∴∠2=∠7.

∵DG平分∠ADF,

∴∠1=∠ADF.

∵∠ADF=∠ABC,

∴∠1=∠2.

∵∠3=∠2,

∴∠1=∠3,

∴DG∥CA.

(2)证明:∵点I是△ABC的内心,

∴∠5=∠6.

由(1)知∠3=∠7.

∴∠4=∠7+∠5=∠3+∠6,

即∠4=∠DAI,

∴AD=ID.

(3)∵∠3=∠7,∠ADE=∠BDA,

∴△DAE∽△DBA,

∴AD∶DB=DE∶DA.

∵BD=DE+BE=9,DE=4,

∴AD∶9=4∶AD,

∴AD=6,

∴DI=6,

∴BI=BD-DI=9-6=3.

中考链接

1.(盐城中考)如图，AB为圆O的弦，∠ADC=35°，则∠CAB的度数为(      )

A.35°     B.45 °     C.55°       D.65°

答案：C

2.(黄石中考)在Rt△ABC中，∠C=90°，CA=8，CB=6，则△ABC的内切圆的周长为           。

答案：4?

学生自主解答，教师讲解答案。

学生自主解答，教师讲解答案。

练中考题型

通过这几道题目来反馈学生对本节所学知识的掌握程度，落实基础。学生刚刚接触到新的知识需要一个过程，也就是对新知识从不熟悉到熟练的过程，无论是基础的习题，还是变式强化，都要以学生理解透彻为最终目标。

分层练习，可以照顾全体学生，让学有余力的学生有更大的进步.

让学生更早的接触中考题型，熟悉考点.

课堂小结

学生归纳本节所学知识

回顾学过的知识，总结本节内容，提高学生的归纳以及语言表达能力。

板书

三角形内切圆

和三角形各边都相切的圆叫做三角形的内切圆。

性质

内心是三角形三条角平分线的交点，所以内心到角的各边的距离相等