









初中数学沪科版九年级下册第24章 圆24.7 弧长与扇形面积24.7.1 弧长与扇形面积精品ppt课件
展开沪科版数学九年级下24.7.1弧长与扇形的面积教学设计
课题 | 弧长与扇形的面积 | 单元 | 24 | 学科 | 数学 | 年级 | 九 |
学习 目标 | 知识与技能目标 1.经历探索弧长计算公式及扇形面积计算公式的过程; 2.了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题 过程与方法目标 1.经历探索弧长计算公式及扇形面积计算公式的过程,培养学生的探索能力; 2.了解弧长及扇形面积公式后,能用公式解决问题,训练学生的数学运用能力. 情感态度与价值观目标 经历探索弧长及扇形面积计算公式.让学生体验教学活动充满着探索与创造,感受数学的严谨性以及数学结论的确定性;通过用弧长及扇形面积公式解决实际问题,让学生体验数学与人类生活的密切联系,激发学生学习数学的兴趣,提高他们的学习积极性,同时提高大家的运用能力. | ||||||
重点 | 经历探索弧长及扇形面积计算公式的过程;了解弧长及扇形面积计算公式;会用公式解决问题. | ||||||
难点 | 探索弧长及扇形面积计算公式;用公式解决实际问题. | ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
导入新课 | 在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位运动员弯路的展直长度相同吗? |
学生思考问题 |
引发学生思考,激发学生的学习兴趣 |
讲授新课 | 师:我们知道,弧是圆的一部分,弧长就是圆周长的一部分.如何计算圆周长?如何计算弧长?
课件展示:
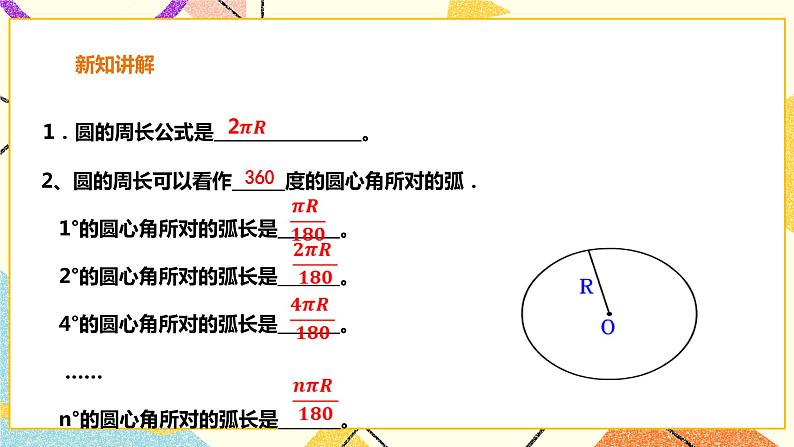
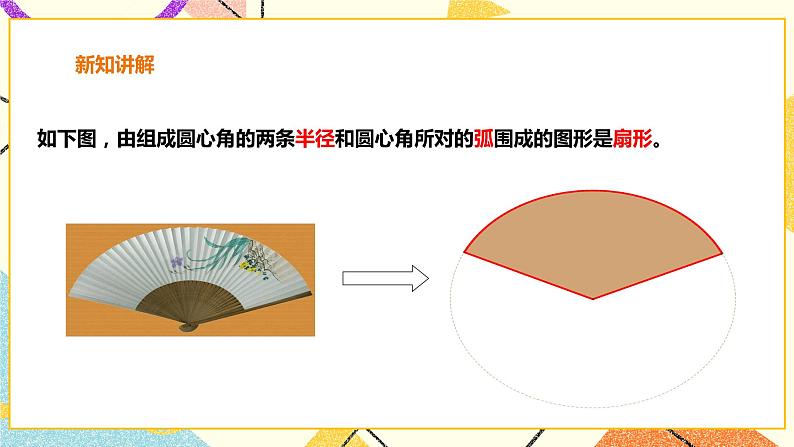
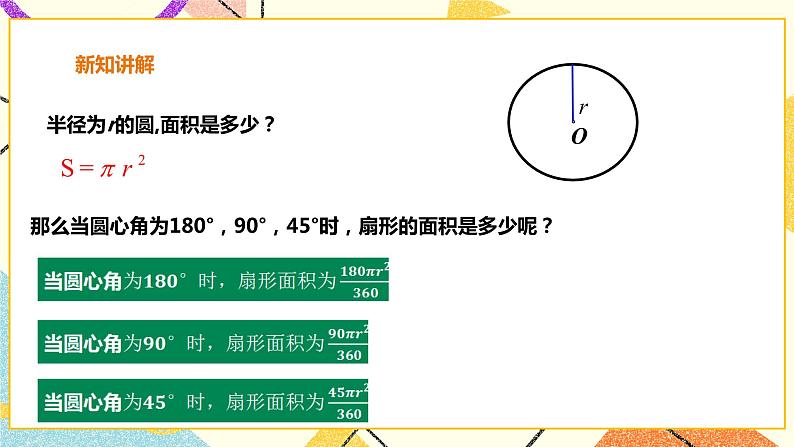
1.圆的周长公式是 。 2、圆的周长可以看作______度的圆心角所对的弧 1°的圆心角所对的弧长是_______。 2°的圆心角所对的弧长是_______。 4°的圆心角所对的弧长是_______。 …… n°的圆心角所对的弧长是_______。 师:由此你能得出弧长公式吗? 生: 若设⊙O半径为R, n°的圆心角所对的弧长为l= 师:运用弧长公式的时候应该注意什么? 生:用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的. 师:如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。 师:想一想:扇形的面积与什么有关? 讨论:怎样从圆的面积公式中找出扇形的面积与扇形的圆心角、半径之间的关系? 师:半径为r的圆面积是多少? 生: s= 那么当圆心角为180°,90°,45°时,扇形的面积是多少呢? 生:,, 师:由此你能得出扇形面积公式吗? 生:半径为R,圆心角为n˚的扇形的面积是 师:比一比: n˚的圆心角所对的弧长和扇形的面积之间有什么关系? 生: 师:对比弧长公式,扇形面积又应该注意什么呢? 生:①公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;②公式要理解记忆(即按照上面推导过程记忆). 课件展示: 例1、一滑轮装置如图,滑轮的半径R=10cm,当重物上升15.7cm时,问滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度?(假设绳索与滑轮之间没有滑动,π取3.14) 例2、古希腊埃拉托塞尼曾给出一个估算地球周长(或子午圈长)的简单方法.如图,点S和点A分别表示埃及的賽伊尼和亚历山大两地,亚历山大在賽伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m).当太阳光线在賽伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为ɑ,实际测得ɑ是7.2°,由此估算出了地球的周长,你能进行计算吗?
|
学生思考,填空,推导出弧长公式
师生共同总结扇形的面积公式
学生自主解答 |
学生通过自己解决问题,充分发挥学习的主动性,同时也培养了学生归纳问题的能力。
通过引导学生自主合作,探究验证,培养学生分析问题和解决问题的意识和能力.
巩固所学知识,培养学生自己解决问题的能力. |
课堂练习 | 1.一个扇形的圆心角是120 ° ,它的面积是3πcm2 ,则这个扇形的半径是( ) 答案:B 2.若扇形的弧长是16cm ,面积是56cm2 ,则它的半径是( ) A.7cm B. 3.5cm C. 2.8cm D.14cm 答案:A 3.如图,☉A、☉B、 ☉C、 ☉D两两不相交,且半径都是2cm,则图中阴影部分的面积是 . 答案:12πcm2 4.已知扇形的圆心角为300,面积为3πcm2 ,则这个扇形的半径R=____ . 答案:6cm 5.如图,圆心角为60°的扇形的半径为10cm.求这个扇形的面积和周长.(精确到0.01cm2和0.01cm) 答案: 解:∵n=60,r=10cm, ∴扇形的面积为S= 扇形的周长为l=2r+ 拓展提升 两个同心圆被两条半径截得的, 又AC=12,求阴影部分的面积. 答案: 解:设OC=r,则OA=r+12,∠O=n° ∴ ∴ ∴OC=18,OA=OC+AC=30 ∴ = ==96π 中考链接 1.(资阳中考)在Rt△ABC中,∠ACB=90°,AC=2,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是 . 答案: 2.(鄂州中考)如图,扇形OAB中,∠AOB=60°,OA=6cm,则图中阴影部分的面积是 。 答案: (6π-9
|
学生自主解答,教师讲解答案。
学生自主解答,教师讲解答案。
练中考题型 |
通过这几道题目来反馈学生对本节所学知识的掌握程度,落实基础。学生刚刚接触到新的知识需要一个过程,也就是对新知识从不熟悉到熟练的过程,无论是基础的习题,还是变式强化,都要以学生理解透彻为最终目标。
分层练习,可以照顾全体学生,让学有余力的学生有更大的进步.
让学生更早的接触中考题型,熟悉考点.
|
课堂小结 | 学生归纳本节所学知识 | 回顾学过的知识,总结本节内容,提高学生的归纳以及语言表达能力。 | |
板书 | 1.定理: 任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆. 2.正多边形及外接圆中的有关概念 中心:一个正多边形的外接圆的圆心. 正多边形的半径: 外接圆的半径. |
|
|
沪科版九年级下册24.7.1 弧长与扇形面积备课ppt课件: 这是一份沪科版九年级下册24.7.1 弧长与扇形面积备课ppt课件,共32页。PPT课件主要包含了与弧长相关的计算,观察与思考,知识要点,弧长公式,典例精析,解弧AB的长为,练一练,圆心角,概念学习,与扇形面积相关的计算等内容,欢迎下载使用。
初中数学沪科版九年级下册24.7.1 弧长与扇形面积获奖ppt课件: 这是一份初中数学沪科版九年级下册24.7.1 弧长与扇形面积获奖ppt课件,文件包含第24章圆247弧长与扇形面积第1课时docx、2472弧长与扇形面积第1课时同步练习docx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
2021学年24.7.1 弧长与扇形面积课文配套课件ppt: 这是一份2021学年24.7.1 弧长与扇形面积课文配套课件ppt,共14页。PPT课件主要包含了C2πR,SπR2等内容,欢迎下载使用。













