



- 2.1 圆的对称性 课件+教案 课件 5 次下载
- 2.2.1 圆心角 课件+教案 课件 5 次下载
- 2.2.2 圆周角 第1课时 圆周角(1) 课件+教案 课件 5 次下载
- 2.2.2 圆周角 第2课时 圆周角(2) 课件+教案 课件 5 次下载
- 2.3 垂径定理 课件+教案 课件 7 次下载
- 2.4 过不共线三点作圆 课件+教案 课件 6 次下载
湘教版九年级下册1.4 二次函数与一元二次方程的联系优质课课件ppt
展开1.4 二次函数与一元二次方程的联系
【知识与技能】
1.掌握二次函数图象与x轴的交点横坐标与一元二次方程两根的关系.
2.理解二次函数图象与x轴的交点的个数与一元二次方程根的个数的关系.
3.会用二次函数图象求一元二次方程的近似根.
4.能用二次函数与一元二次方程的关系解决综合问题.
【过程与方法】
经历探索二次函数与一元二次方程的关系的过程,体会二次函数与方程之间的联系,进一步体会数形结合的思想.
【情感态度】
通过自主学习,小组合作,探索出二次函数与一元二次方程的关系,感受数学的严谨性,激发热爱数学的情感.
【教学重点】
①理解二次函数与一元二次方程的联系.
②求一元二次方程的近似根.
【教学难点】
一元二次方程与二次函数的综合应用.
一、情境导入,初步认识
1.一元二次方程ax2+bx+c=0的实数根,就是二次函数y=ax2+bx+c当 y=0 时,自变量x的值,它是二次函数的图象与x轴交点的 横坐标 .
2.抛物线y=ax2+bx+c与x轴交点个数与一元二次方程ax2+bx+c=0根的判别式的关系:当b2-4ac<0时,抛物线与x轴 无 交点;当b2-4ac=0时,抛物线与x轴有 一 个交点;当b2-4ac>0时,抛物线与x轴有 两 个交点.
学生回答,教师点评
二、思考探究,获取新知
探究1 求抛物线y=ax2+bx+c与x轴的交点
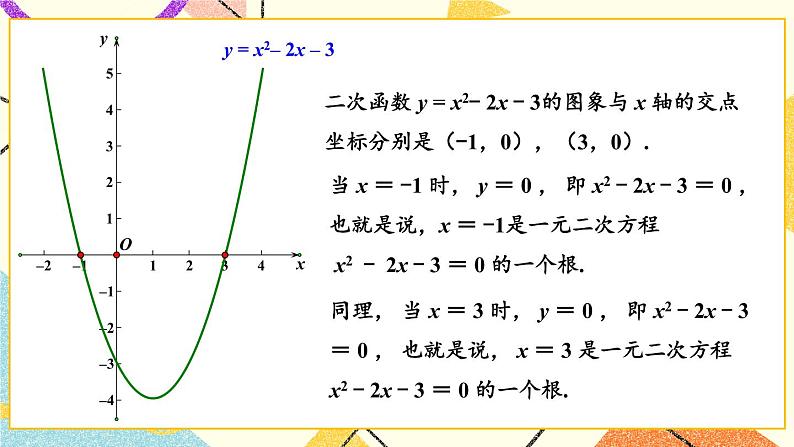
例1 求抛物线y=x2-2x-3与x轴交点的横坐标.
【分析】抛物线y=x2-2x-3与x轴相交时,交点的纵坐标y=0,转化为求方程x2-2x-3=0的根.
解:因为方程x2-2x-3=0的两个根是x1=3,x2=-1,所以抛物线y=x2-2x-3与x轴交点的横坐标分别是3或-1.
【教学说明】求抛物线与x轴的交点坐标,首先令y=0,把二次函数转化为一元二次方程,求交点的横坐标就是求此方程的根.
探究2 抛物线与x轴交点的个数与一元二次方程的根的个数之间的关系思考:
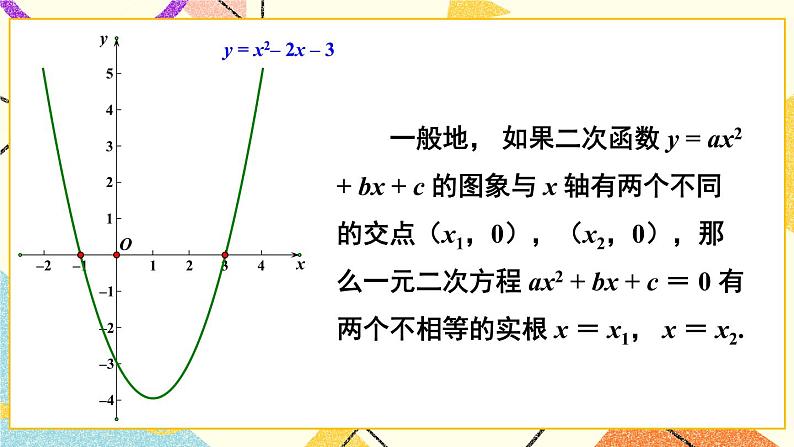
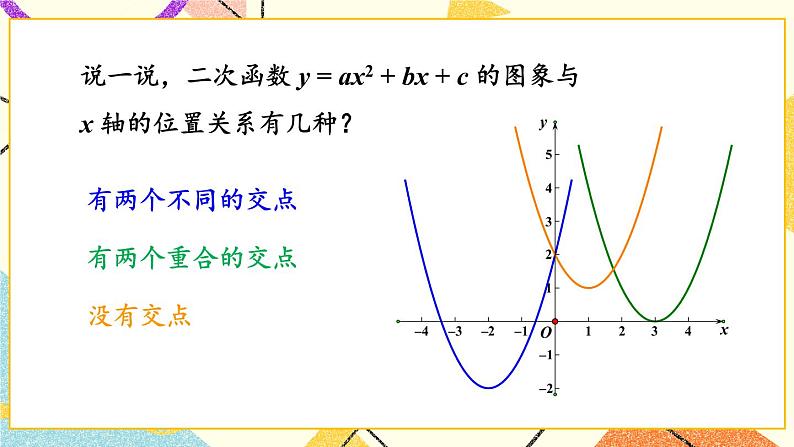
(1)你能说出函数y=ax2+bx+c(a≠0)的图象与x轴交点个数的情况吗?猜想交点个数和方程ax2+bx+c=0(a≠0)的根的个数有何关系?
(2)一元二次方程ax2+bx+c=0(a≠0)的根的个数由什么来判断?
【教学说明】
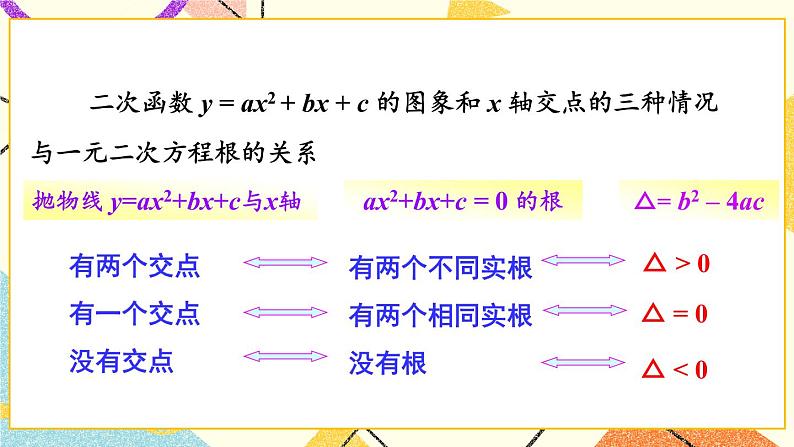
抛物线y=ax2+bx+c(a≠0)与x轴的位置关系 | 一元二次方程ax2+bx+c=0(a≠0)根的情况 | b2-4ac的值 |
有两个公共点 | 有两个不相等的实数根 | b2-4ac>0 |
只有一个公共点 | 有两个相等的实数根 | b2-4ac=0 |
无公共点 | 无实数根 | b2-4ac<0 |
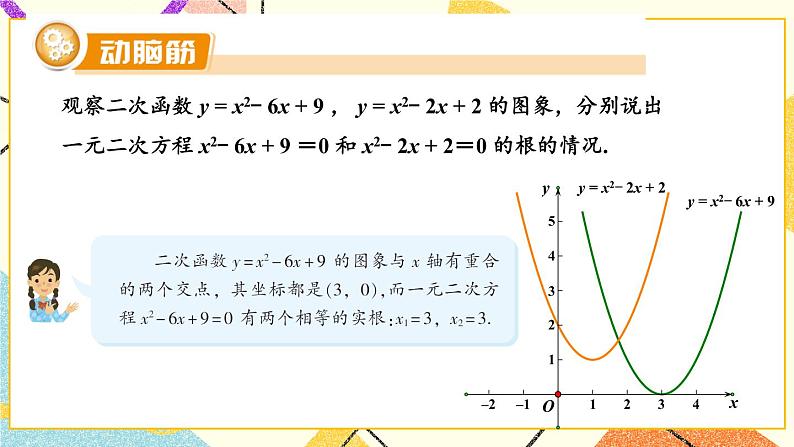
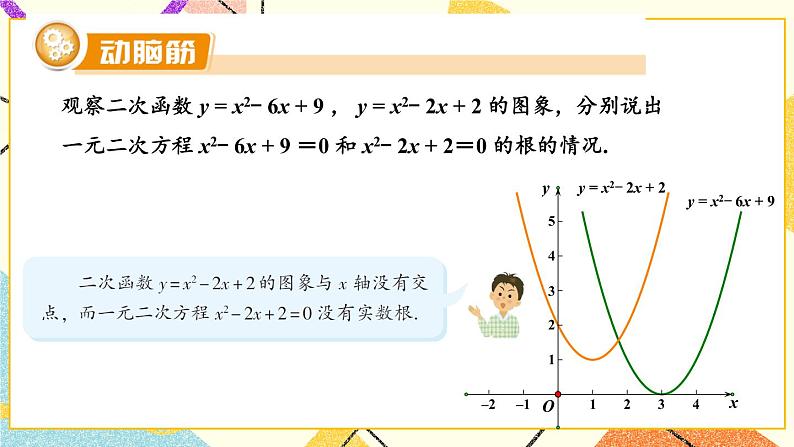
探究3 利用函数图象求一元二次方程的近似根
提出问题:同学们可以估算下一元二次方程x2-2x-2=0的两根是什么?
学生回答:
【教学点评】-1<x1<0,2<x2<3.
探究4 一元二次方程与相应二次函数的综合应用
讲解教材P26例2
【教学说明】已知二次函数y=ax2+bx+c(a≠0)的某一个函数值y=M,求对应的自变量的值时,需要解一元二次方程ax2+bx+c=M,这样将二次函数的知识和前面学的一元二次方程就紧密联系起来了.
三、运用新知,深化理解
1.(广东中山中考)已知抛物线y=ax2+bx+c的图象如图所示,则关于x的方程ax2+bx+c=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.有两个同号的实数根
D.没有实数根
2.若一元二次方程x2-mx+n=0无实根,则抛物线y=-x2+mx-n图象位于( )
A.x轴上方 B.第一、二、三象限
C.x轴下方 D.第二、三、四象限
3.(x-1)(x-2)=m(m>0)的两根为α,β,则α,β的范围为( )
A.α<1,β>2 B.α<1<β<2
C.1<α<2<β D.α<1,β>2
4.二次函数y=ax2+bx+c与x轴的交点坐标为(1,0),(3,0),则方程ax2+bx+c=0的解为 .
5.(湖北武汉中考)已知二次函数y=x2-(m+1)x+m的图象交x轴于A(x1,0),B(x2,0)两点,交y轴的正半轴于点C,且x21+x22=10.
(1)求此二次函数的解析式;
(2)是否存在过点D(0,-)的直线与抛物线交于点M、N,与x轴交于点E,使得点M、N关于点E对称?若存在,求出直线MN的解析式;若不存在,请说明理由.
学生解答:
【答案】1.D 2.C 3.D 4.x1=1,x2=3
5.解:(1)y=x2-4x+3 (2)存在 y=x-
【教学说明】一元二次方程的根的情况和二次函数与x轴的交点个数之间的关系是相互的,根据根的情况可以判断交点个数,反之也成立.
四、师生互动,课堂小结
1.这节课你学到了什么?还有哪些疑惑?
2.在学生回答基础上,教师点评:
①求二次函数自变量的值与一元二次方程根的关系;
②抛物线与x轴交点个数与一元二次方程根的个数的关系.
③用函数图象求“一元二次方程的近似根”;
④二次函数问题可转化为对应一元二次方程根与系数关系问题.
1.教材P28第1~3题.
2.完成同步练习册中本课时的练习.
通过本节课的学习,让学生用函数的观点解方程和用方程的知识求函数,取某一特值时,把对应的自变量的值都联系起来了,这样对二次函数的综合应用就方便得多了,从中让学生体会到各知识之间是相互联系的这一最简单的数学道理.
数学九年级下册第1章 二次函数1.4 二次函数与一元二次方程的联系优秀ppt课件: 这是一份数学九年级下册<a href="/sx/tb_c104131_t3/?tag_id=26" target="_blank">第1章 二次函数1.4 二次函数与一元二次方程的联系优秀ppt课件</a>,文件包含湘教版数学九年级下册14《二次函数与一元二次方程的联系》课件pptx、湘教版数学九年级下册14《二次函数与一元二次方程的联系》教案doc等2份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
湘教版九年级下册1.4 二次函数与一元二次方程的联系习题ppt课件: 这是一份湘教版九年级下册1.4 二次函数与一元二次方程的联系习题ppt课件,共23页。
数学湘教版第1章 二次函数1.4 二次函数与一元二次方程的联系习题ppt课件: 这是一份数学湘教版第1章 二次函数1.4 二次函数与一元二次方程的联系习题ppt课件,共17页。













