沪教版 (五四制)九年级下册27.2 圆心角、弧、弦、弦心距之间的关系获奖课件ppt

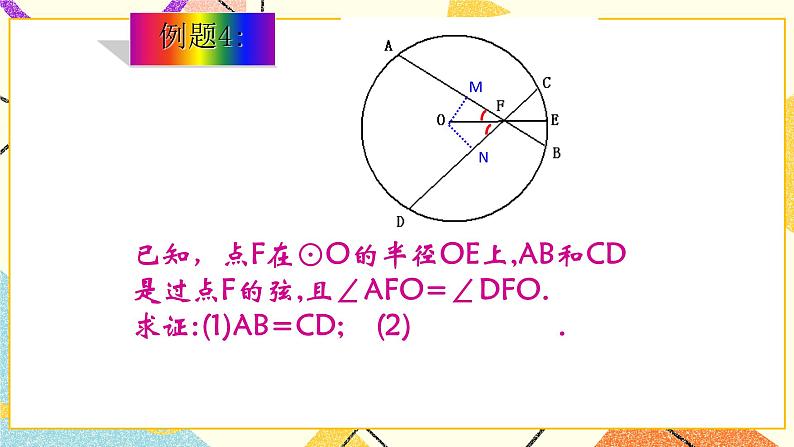
一、复习引入

问1：结合图形说出圆心角、弧、弦、弦心距之间的关系？

在⊙O中，AB和AB是弦，于点C，于点C’，

(1) ∠AOB=∠A'OB'；(2)  AB=A'B'

(3) ；(4) OC=OC’.

二、探索新知

例题4  已知点F在圆O的半径OE上，

AB和CD过点F的弦，∠AFO=∠DFO  ，

求证：（1）AB=CD；（2）．

分析：要证明结论AB=CD，由已知

条件∠AFO=∠DFO想到什么？

证明：（1）过点O分别作OM⊥AB ，ON⊥CD，垂足分别为M、N．则OM、ON分别表示AB和CD的弦心距．

∵∠AFO=∠DFO，

∴ OM=ON．

∴AB=CD．

（2）∵AB=CD，

∴．

变式：若点F是⊙O的半径OE的延长线上的一点，其它条件不变，结论是否成立？

反馈练习：练习27.2（3）第1、2题

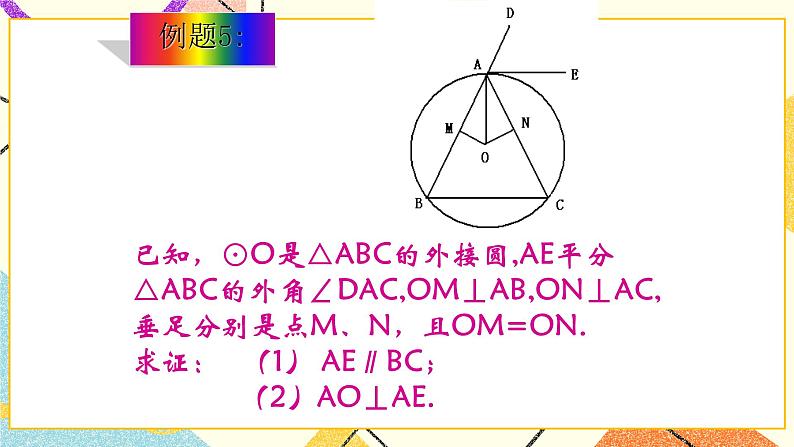
例题5  已知：⊙O是△ABC的外接圆，AE平分△ABC的外角∠DAC，OM⊥AB，ON⊥AC，垂足分别是点M、N，且OM＝ON．

求证：（1）AE∥BC；（2）AO⊥AE．

分析：(根据条件，图形分解为两个基本图形)

证明：（1）∵OM⊥AB，ON⊥AC，OM=ON．

∴ AB=CD，

∴ ∠B=∠C．

∵∠DAC=∠B+∠C，

∴∠DAC=2∠B，

∵AE平分∠DAC，

∴∠DAC=2∠DAE，

∴2∠DAE=2∠B，

∴ ∠DAE=∠B．

∴ AE∥BC．

（2）∵OM⊥AB，ON⊥AC，垂足分别是点M、N，且OM＝ON，

∴点O在∠BAC平分线上，

即AO平分∠BAC，

得∠BAC=2∠CAO．

∵2∠CAO +2∠CAE =180°，

∴∠EAC+∠CAO=90°，

∴AO⊥AE．

反馈练习：练习27.2（3）第3题

小结：

证明两条直线互相垂直常用的方法：

（1）直接计算角为90°；

（2）证明这个角和一个直角相等；

（3）等腰三角形的三线合一性质．

四、课堂小结

谈谈这节课你有什么收获?

五、布置作业

练习册  习题27.2（3）