初中数学人教版七年级下册5.1.2 垂线教学课件ppt

这是一份初中数学人教版七年级下册5.1.2 垂线教学课件ppt，共31页。PPT课件主要包含了温故知新，素养目标，课堂导入，新知探究，垂线定义，垂直的表示方法，符号语言，跟踪练习，2用量角器画，解如图所示等内容，欢迎下载使用。

1.如图，直线 a，b 相交，则∠1 的对顶角为 ，∠1 的邻补角有 . 2.如图，直线a,b相交，若∠1=30°，则∠2= ，∠3= .
1.理解和掌握垂线的概念.2.能用三角尺或量角器过一点画已知直线的垂线，培养学生画图的基本技能.3.从实际问题中发现“在同一平面内，过一点有且只有一条直线与已知直线垂直”的性质，培养学生发现问题的能力.4.通过学习垂直的表示方法，使学生建立初步的符号感。
前面我们复习了两条相交直线所成的角，如果两条直线相交成特殊角直角时，这两条直线有怎样的特殊的位置关系呢？日常生活中有没有这方面的实例呢？ 下面我们就来研究这个问题.
知识点1: 垂线的概念
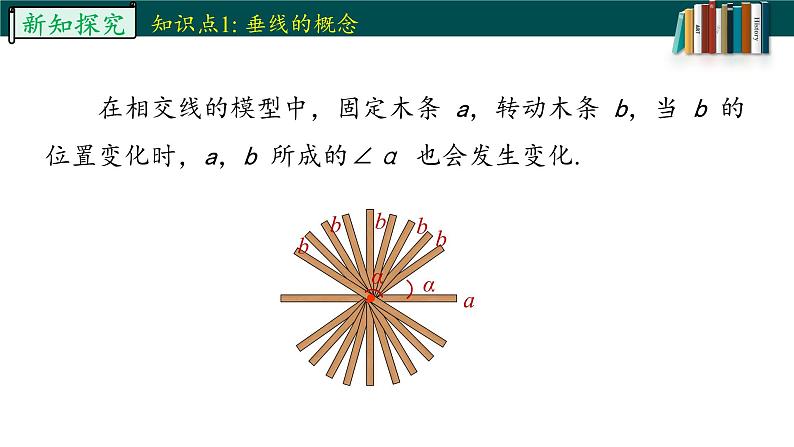
在相交线的模型中，固定木条 a，转动木条 b，当 b 的位置变化时，a，b 所成的∠α 也会发生变化.
如图，当∠AOC＝90° 时，∠BOD,∠AOD,∠BOC 的度数是多少？
由对顶角和邻补角的性质可知，当∠AOC＝90°时，∠BOD=∠AOD=∠BOC=90°.
两条直线相交成四个角，如果有一个角是直角，那么称这两条直线互相垂直.其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足.
注意：1.两条直线互相垂直是它们相交的一种特殊情况. 2.两条线段互相垂直是指这两条线段所在的直线互相垂直.
如图，直线 AB 与 CD 相交于点 O，若∠BOC = 90°，则AB，CD 互相垂直，记作“AB⊥CD”，读作“AB 垂直于 CD”，直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线)，交点 O 叫做垂足.
如果用 l，m 表示这两条直线，那么直线 l 与直线 m 垂直，可记作：l⊥m (或 m⊥l ).
如图，当直线AB与CD相交于O点，∠AOD=90°时，AB⊥CD，垂足为O.
①判定：∵∠AOD=90°,（已知） ∴AB⊥CD.（垂直的定义）
反之，若直线AB与CD垂直,垂足为O，则∠AOD=90°.
②性质：∵ AB⊥CD ,（已知） ∴ ∠AOD=90° .（垂直的定义）
(∠AOC=∠BOC=∠BOD=90°)
知识点2: 垂线的画法及性质
(1)画已知直线l的垂线能画几条？ (2)过直线 l 上的一点A画l的垂线，这样的垂线能画几条？ (3)过直线 l 外的一点B画l的垂线，这样的垂线能画几条？
1.落.2.移.3.画.
如图，已知直线 l 和 l 上的一点 A，过点 A 作 l 的垂线.
这样画直线 l 的垂线可以画几条？
如图，已知直线 l 和 l 外的一点 A ，过点 A 作 l 的垂线.
经过一点画已知直线的垂线，通常有两种画法.(1)用三角尺画：1.落：让三角尺的一条直角边落在已知直线上，使其与已知直线重合.2.移：沿已知直线移动三角尺，使其另一条直角边经过已知点.3.画：沿此直角边画直线，则这条直线就是已知直线的垂线.
垂线的性质1：在同一平面内，过一点有且只有一条直线与已知直线垂直.
注意：1.不能忽略“在同一平面内”这个条件，因为如果不在同一平面内，那么过一点有无数条直线与已知直线垂直.2.“过一点”中的点，可以在已知直线上，也可以在已知直线外；3.“有且只有”中，“有”指存在，“只有”指唯一性.4.画一条线段或射线的垂线，就是画它们所在直线的垂线，垂足可能在这条线段或射线上，也可能在线段的延长线上或射线的反向延长线上.
A. &1& B. &2& C. &3& D. &4&
1.定义：两条直线相交成四个角，如果有一个角是直角，那么称这两条直线互相垂直.其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足.
2.垂线的性质1：在同一平面内，过一点有且只有一条直线与已知直线垂直.
1. 如图,AB⊥AC,已知∠1=33°,则∠2的度数是 (　　)A.33° B.57°C.67° D.167°
2.如图，AO⊥CO，直线 BD 经过点 O，且∠1 =20°，则∠COD 的度数为( )A.70°B.110°C.140°D.160°
在同一平面内，过一点有且只有一条直线与已知直线垂直
1. 如图,直线AB,CD相交于点O,给出下列条件:①∠AOD=90°;②∠AOC=∠BOC;③∠AOC=∠BOD.其中能说明AB⊥CD的有(　　)A.①②B.①③C.②③D.①②③
2. 如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为 (　　)A.26°B.36°C.44°D.54°
3. 如图,已知OA⊥OC,OB⊥OD,则图中有　　　　对相等的角. 
4. 如图,直线AB,CD相交于点O,OE平分∠AOD,FO⊥CD于点O,∠1=40°,则∠2的度数为　　　　. 
5. 已知OA⊥OC,∠AOB∶∠BOC=1∶4,则∠BOC的度数为(　　)A.54° B.54°或120°C.72° 或120° D.54°或72°
6. 已知直线AB和CD相交于点O,OE⊥AB于点O ,OF⊥CD于点O ,∠BOF=25°,则∠AOC与∠EOD的度数分别为　　　　　. 
7. 如图,已知直线AB,CD相交于点O,且OE⊥AB.(1)过点O作CD的垂线MN;(2)若点F是(1)中所作直线MN上任意一点(O点除外),且∠AOC=34°,求∠EOF的度数.
7. 解:(1)如图所示.
(2)分两种情况讨论:
②如图2,当点F在射线ON上时,∵OE⊥AB,∴∠EOB=90°,∵MN⊥CD,∴∠MOC=∠AOC+∠AOM=90°,∴∠AOM=90°-∠AOC=56°,∴∠BON=∠AOM=56°,∴∠EOF=∠EOB+∠BON=90°+56°=146°.
综上,∠EOF的度数是34°或146°.
①如图1,当点F在射线OM上时,∵EO⊥AB,MN⊥CD,∴∠EOB=∠MOD=90°,∴∠MOE+∠EOD=90°,∠EOD+∠BOD=90°,∴∠EOF=∠BOD=∠AOC=34°.