






还剩22页未读,
继续阅读
所属成套资源:七年级数学下册同步精品随堂教学课件
成套系列资料,整套一键下载
人教版七年级下册5.3.1 平行线的性质教学课件ppt
展开
这是一份人教版七年级下册5.3.1 平行线的性质教学课件ppt,共30页。PPT课件主要包含了温故知新,两直线平行,素养目标,课堂导入,新知探究,∵a∥b已知,应用格式,同位角相等,内错角相等,同旁内角互补等内容,欢迎下载使用。
1.同位角相等2.内错角相等3.同旁内角互补
平行线的判定方法是什么?
根据右图,填空:① 如果∠1=∠5, 那么 ∥ .( )② 如果∠2=∠3 , 那么 ∥ .( )③ 如果∠1+∠4=180°, 那么 ∥ .( )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
l₁ l₂
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2.能根据平行线的性质进行简单的推理.
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,同位角、内错角、同旁内角又各有什么关系呢? 这就是我们下面要学习的平行线的性质. 类似于研究平行线的判定,我们先来研究两条直线平行时,它们被第三条直线截得的同位角质关系.
知识点: 平行线的性质
画两条平行线 a//b,然后画一条截线 c 与 a,b 相交,标出如图所示的角. 度量所形成的 8 个角的度数,把结果填入下表:
∠1, ∠2,⋯,∠8中,哪些是同位角?它们的度数之间有什么关系?由此猜想两条平行线被第三条直线截得的同位角有什么关系?
猜想 两条平行线被第三条直线所截,同位角相等.
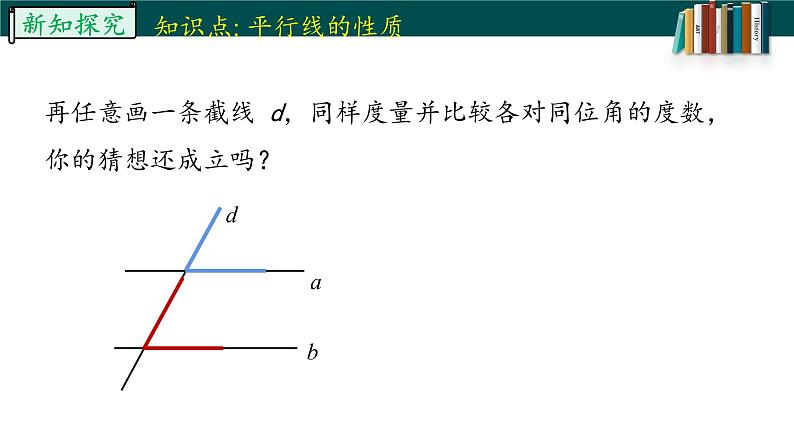
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
如果两直线不平行,上述结论还成立吗?
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.
∴∠1=∠2 (两直线平行,同位角相等)
在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等, 能否得到内错角之间的数量关系?
如图,已知 a//b,那么2 与3 相等吗?为什么?
解:∵ a∥b,(已知)∴∠1=∠2.(两直线平行,同位角相等)又∵ ∠1=∠3,(对顶角相等)∴ ∠2=∠3.(等量代换)
如图,已知 a//b,那么2 与4 有什么关系呢?为什么?
解: ∵a//b ,(已知)
∴ 1= 2.(两直线平行,同位角相等)
∵ 1+ 4=180°,(邻补角互补)
∴ 2+ 4=180°.(等量代换)
类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
性质3:两条平行线被第三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
解:∵梯形上、下底互相平行,∴∠A 与∠D 互补,∠B 与∠C 互补.
即梯形的另外两个角分别是 80°,65°.
∴∠D=180 °-∠A=180°-100°=80°, ∠C= 180 °-∠B=180°-115°=65°.
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
平行线的判定和性质的区别和联系联系:平行线的判定和性质反映了角的数量关系和直线的位置关系之间的相互转换.区别:平行线的判定以两直线平行为结论,即由两角相等或互补得到两直线平行,是由数量关系得到位置关系;平行线的性质以两直线平行为条件,即由两直线平行得到两角相等或互补,是由位置关系得到数量关系.
1.[2022凉山州中考]如图,直线a∥b,c是截线,若∠1=50°,则∠2= ( )A.40°B.45°C.50° D.55°
2. [2022达州中考]如图,AB∥CD,直线EF分别交AB,CD于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=80°,则∠PNM等于 ( )A.15°B.25°C.35°D.45°
3. [2022大连中考]如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF的度数是 ( )A.35°B.55°C.70°D.110°
4.[2022娄底中考]一杆古秤在称物时的状态如图所示,已知∠1=80°,则∠2= ( )A.20°B.80°C.100°D.120°
5.[2021岳阳中考]将一副直角三角板按如图方式摆放,若直线a∥b,则∠1的大小为( )A.45° B.60°C.75°D.105°
6.[2021济宁中考]如图,AB∥CD,BC∥DE.若∠B=72°28',那么∠D的度数是 ( )A.72°28' B.101°28'C.107°32' D.127°32'
1. [2022乐山中考]如图,已知直线a∥b,∠BAC=90°,∠1=50°.则∠2= °.
2. [2022临沂期末]将三角板的直角顶点按如图所示摆放在直尺的一边上,则下列结论不一定正确的是 ( )A.∠1+∠3=90°B.∠2+∠3=90°C.∠2+∠4=180°D.∠1=∠2
3. [2022武汉黄陂区期中]光在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,若∠1=48°,∠2=158°,则∠3的度数为 ( )A.68°B.70°C.78°D.80°
4.如图,CD//AB,点 O 在 AB 上,OE 平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的度数是( )A.20° B.25° C.30° D.35°
5. [2022兴安盟期末]如图,已知AB∥CD,∠ABD的平分线BF和∠BDC的平分线DE交于点E,BF交CD于点F.(1)求∠1+∠2的度数;(2)若∠2=40°,求∠3的度数.
解:(1)因为BF,DE分别平分∠ABD和∠BDC,所以∠ABD=2∠1,∠BDC=2∠2.因为AB∥CD,所以∠ABD+∠BDC=180°,即2∠1+2∠2=180°,所以∠1+∠2=90°.
(2)因为∠2=40°,由(1)知∠1+∠2=90°,所以∠1=90°-∠2=50°.因为AB∥CD,所以∠1+∠3=180°,所以∠3=180°-∠1=130°.
6. [2022洛阳涧西区期中]【课题学习】平行线的“等角转化”功能. 【问题解决】(1)阅读并补充上述解题过程.【解题反思】从上面的解题过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】(2)如图2,已知AB∥CD,∠BEC=80°,求∠B-∠C的度数.(提示:过点E作AB或CD的平行线)【深化拓展】(3)如图3,已知AB∥CD,BF,CG分别平分∠ABE,∠DCE,且所在直线交于点F,∠BEC=80°,则∠F的度数为 .
6. 解:(1)∠EAB ∠DAC(2)如图1,过点E作HE∥AB,∵AB∥CD,∴HE∥CD,∴∠B+∠BEH=180°,∠HEC=∠C,∴∠B+∠BEH+∠HEC=180°+∠C,∴∠B-∠C=180°-∠BEC=180°-80°=100°.
(3)如图2,过点E作EM∥AB,过点F作FN∥CD,∵AB∥CD,∴AB∥ME∥CD∥FN,∵BF平分∠ABE,CG平分∠ECD,∴∠ABF=∠EBF,∠ECG=∠DCG.设∠ABF=∠EBF=α,∠ECG=∠DCG=β,∵AB∥ME∥CD∥FN,∴∠BFN=∠ABF=α,∠CFN=∠GCD=β,∠BEM+∠ABE=180°,∠MEC=∠ECD=2β,∴∠BEM=180°-2α,∵∠BEM+∠MEC=∠BEC=80°,∴180°-2α+2β=80°,∴α-β=50°,∴∠BFG=∠BFN-∠CFN=α-β=50°.
1.同位角相等2.内错角相等3.同旁内角互补
平行线的判定方法是什么?
根据右图,填空:① 如果∠1=∠5, 那么 ∥ .( )② 如果∠2=∠3 , 那么 ∥ .( )③ 如果∠1+∠4=180°, 那么 ∥ .( )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
l₁ l₂
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2.能根据平行线的性质进行简单的推理.
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,同位角、内错角、同旁内角又各有什么关系呢? 这就是我们下面要学习的平行线的性质. 类似于研究平行线的判定,我们先来研究两条直线平行时,它们被第三条直线截得的同位角质关系.
知识点: 平行线的性质
画两条平行线 a//b,然后画一条截线 c 与 a,b 相交,标出如图所示的角. 度量所形成的 8 个角的度数,把结果填入下表:
∠1, ∠2,⋯,∠8中,哪些是同位角?它们的度数之间有什么关系?由此猜想两条平行线被第三条直线截得的同位角有什么关系?
猜想 两条平行线被第三条直线所截,同位角相等.
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
如果两直线不平行,上述结论还成立吗?
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.
∴∠1=∠2 (两直线平行,同位角相等)
在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等, 能否得到内错角之间的数量关系?
如图,已知 a//b,那么2 与3 相等吗?为什么?
解:∵ a∥b,(已知)∴∠1=∠2.(两直线平行,同位角相等)又∵ ∠1=∠3,(对顶角相等)∴ ∠2=∠3.(等量代换)
如图,已知 a//b,那么2 与4 有什么关系呢?为什么?
解: ∵a//b ,(已知)
∴ 1= 2.(两直线平行,同位角相等)
∵ 1+ 4=180°,(邻补角互补)
∴ 2+ 4=180°.(等量代换)
类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
性质3:两条平行线被第三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
解:∵梯形上、下底互相平行,∴∠A 与∠D 互补,∠B 与∠C 互补.
即梯形的另外两个角分别是 80°,65°.
∴∠D=180 °-∠A=180°-100°=80°, ∠C= 180 °-∠B=180°-115°=65°.
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
平行线的判定和性质的区别和联系联系:平行线的判定和性质反映了角的数量关系和直线的位置关系之间的相互转换.区别:平行线的判定以两直线平行为结论,即由两角相等或互补得到两直线平行,是由数量关系得到位置关系;平行线的性质以两直线平行为条件,即由两直线平行得到两角相等或互补,是由位置关系得到数量关系.
1.[2022凉山州中考]如图,直线a∥b,c是截线,若∠1=50°,则∠2= ( )A.40°B.45°C.50° D.55°
2. [2022达州中考]如图,AB∥CD,直线EF分别交AB,CD于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=80°,则∠PNM等于 ( )A.15°B.25°C.35°D.45°
3. [2022大连中考]如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF的度数是 ( )A.35°B.55°C.70°D.110°
4.[2022娄底中考]一杆古秤在称物时的状态如图所示,已知∠1=80°,则∠2= ( )A.20°B.80°C.100°D.120°
5.[2021岳阳中考]将一副直角三角板按如图方式摆放,若直线a∥b,则∠1的大小为( )A.45° B.60°C.75°D.105°
6.[2021济宁中考]如图,AB∥CD,BC∥DE.若∠B=72°28',那么∠D的度数是 ( )A.72°28' B.101°28'C.107°32' D.127°32'
1. [2022乐山中考]如图,已知直线a∥b,∠BAC=90°,∠1=50°.则∠2= °.
2. [2022临沂期末]将三角板的直角顶点按如图所示摆放在直尺的一边上,则下列结论不一定正确的是 ( )A.∠1+∠3=90°B.∠2+∠3=90°C.∠2+∠4=180°D.∠1=∠2
3. [2022武汉黄陂区期中]光在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,若∠1=48°,∠2=158°,则∠3的度数为 ( )A.68°B.70°C.78°D.80°
4.如图,CD//AB,点 O 在 AB 上,OE 平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的度数是( )A.20° B.25° C.30° D.35°
5. [2022兴安盟期末]如图,已知AB∥CD,∠ABD的平分线BF和∠BDC的平分线DE交于点E,BF交CD于点F.(1)求∠1+∠2的度数;(2)若∠2=40°,求∠3的度数.
解:(1)因为BF,DE分别平分∠ABD和∠BDC,所以∠ABD=2∠1,∠BDC=2∠2.因为AB∥CD,所以∠ABD+∠BDC=180°,即2∠1+2∠2=180°,所以∠1+∠2=90°.
(2)因为∠2=40°,由(1)知∠1+∠2=90°,所以∠1=90°-∠2=50°.因为AB∥CD,所以∠1+∠3=180°,所以∠3=180°-∠1=130°.
6. [2022洛阳涧西区期中]【课题学习】平行线的“等角转化”功能. 【问题解决】(1)阅读并补充上述解题过程.【解题反思】从上面的解题过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】(2)如图2,已知AB∥CD,∠BEC=80°,求∠B-∠C的度数.(提示:过点E作AB或CD的平行线)【深化拓展】(3)如图3,已知AB∥CD,BF,CG分别平分∠ABE,∠DCE,且所在直线交于点F,∠BEC=80°,则∠F的度数为 .
6. 解:(1)∠EAB ∠DAC(2)如图1,过点E作HE∥AB,∵AB∥CD,∴HE∥CD,∴∠B+∠BEH=180°,∠HEC=∠C,∴∠B+∠BEH+∠HEC=180°+∠C,∴∠B-∠C=180°-∠BEC=180°-80°=100°.
(3)如图2,过点E作EM∥AB,过点F作FN∥CD,∵AB∥CD,∴AB∥ME∥CD∥FN,∵BF平分∠ABE,CG平分∠ECD,∴∠ABF=∠EBF,∠ECG=∠DCG.设∠ABF=∠EBF=α,∠ECG=∠DCG=β,∵AB∥ME∥CD∥FN,∴∠BFN=∠ABF=α,∠CFN=∠GCD=β,∠BEM+∠ABE=180°,∠MEC=∠ECD=2β,∴∠BEM=180°-2α,∵∠BEM+∠MEC=∠BEC=80°,∴180°-2α+2β=80°,∴α-β=50°,∴∠BFG=∠BFN-∠CFN=α-β=50°.













