专题04 翘脚模型（解析版）

这是一份专题04 翘脚模型（解析版），共32页。试卷主要包含了基础知识回顾，模型的概述等内容，欢迎下载使用。

专题04 翘脚模型
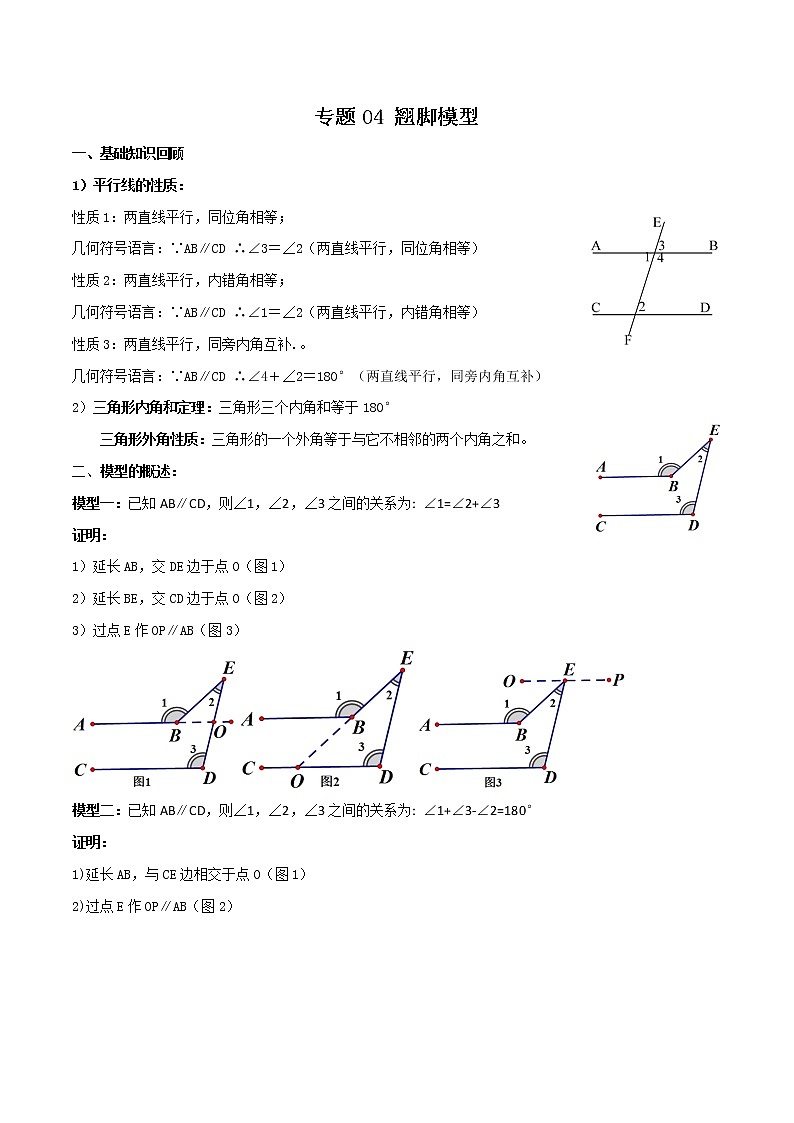
一、基础知识回顾
1）平行线的性质：
性质1：两直线平行，同位角相等；
几何符号语言：∵AB∥CD ∴∠3＝∠2（两直线平行，同位角相等）
性质2：两直线平行，内错角相等；
几何符号语言：∵AB∥CD ∴∠1＝∠2（两直线平行，内错角相等）
性质3：两直线平行，同旁内角互补.。
几何符号语言：∵AB∥CD ∴∠4＋∠2＝180°（两直线平行，同旁内角互补）
2）三角形内角和定理：三角形三个内角和等于180°
三角形外角性质：三角形的一个外角等于与它不相邻的两个内角之和。
二、模型的概述：
模型一：已知AB∥CD，则∠1，∠2，∠3之间的关系为: ∠1=∠2+∠3
证明：
1）延长AB，交DE边于点O（图1）
2）延长BE，交CD边于点O（图2）
3）过点E作OP∥AB（图3）

模型二：已知AB∥CD，则∠1，∠2，∠3之间的关系为: ∠1+∠3-∠2=180°
证明：
1)延长AB，与CE边相交于点O（图1）
2)过点E作OP∥AB（图2）

【基础过关练】
1．如图，如果AB∥EF，EF∥CD，则∠1，∠2，∠3的关系式__________．

【答案】∠2+∠3﹣∠1=180°
【分析】根据平行线的性质和平角定义求解即可．
【详解】解：∵AB∥EF，EF∥CD，
∴∠2+∠BOE=180°，∠3+∠COF=180°，
∴∠2+∠3+∠BOE+∠COF=360°，
∵∠BOE+∠COF+∠1=180°，
∴∠BOE+∠COF=180°﹣∠1，
∴∠2+∠3+（180°﹣∠1）=360°，
即∠2+∠3﹣∠1=180°．
故答案为：∠2+∠3﹣∠1=180°．
【点睛】本题考查平行线的性质、平角定义，熟练掌握平行线的性质是解答的关键．
2．如图所示，AB∥CD，∠E＝37°，∠C＝ 20°，则∠EAB的度数为__________．

【答案】57°
【分析】根据三角形内角和180°以及平行线的性质：1、如果两直线平行，那么它们的同位角相等；2、如果两直线平行，那么它们的同旁内角互补；3、如果两直线平行，那么它们的内错角相等，据此计算即可．
【详解】解：设AE、CD交于点F，

∵∠E＝37°，∠C＝ 20°，
∴∠CFE=180°-37°-20°=123°，
∴∠AFD=123°，
∵AB∥CD，
∴∠AFD+∠EAB=180°，
∴∠EAB=180°-123°=57°，
故答案为：57°．
【点睛】本题主要考查三角形内角和定理以及平行线的性质，熟知平行的性质是解题的关键．
3．如图，已知∠ABC=80°，∠CDE=140°，则∠BCD=_____．

【答案】
【分析】延长交BC于M，根据两直线平行，内错角相等证明∠BMD=∠ABC，再求解，再利用三角形的外角的性质可得答案．
【详解】解：延长交BC于M，
∵
∴∠BMD=∠ABC=80°，
∴；
又∵∠CDE=∠CMD+∠C，
∴．

故答案是：40°
【点睛】本题考查了平行线的性质．三角形的外角的性质，邻补角的定义，掌握以上知识是解题的关键．
4．如图，，于点．若，则的度数为_______．

【答案】
【分析】是的外交，通过平行和平角的关系求出，即可求解的度数．
【详解】解：如图所示，

∵，，
∴，
∵，
∴，
∵是的外角，且，即，
∴，
故答案为：．
【点睛】本题主要考查平行线的性质，三角形外交的性质，掌握平行线的性质，三角形的外交等于与它不相邻的两个内角的和是解题的关键．
5．如图，直线，直线AB交，于D，B两点，交直线于点C．若，则__________．

【答案】110°##110度
【分析】利用垂直定义和三角形内角和定理计算出∠ADC的度数，再利用平行线的性质可得∠3的度数，再根据邻补角的性质可得答案．
【详解】解：如图所示：

∵AC⊥AB，
∴∠A=90°，
∵∠1=20°，
∴∠ADC=180°-90°-20°=70°，
∵，
∴∠3=∠ADC=70°，
∴∠2=180°-70°=110°，
故答案为：110°．
【点睛】此题主要考查了平行线的性质，三角形内角定理，垂直的定义，关键是掌握两直线平行，同位角相等．
6．如图，直线，是直线上一点，是直线外一点，若，，则的度数为________．

【答案】##120度
【分析】直接利用平行线的性质并结合三角形内角和定理即可得出答案．
【详解】解：延长交于点，
∵，，，
∴，
∵，
∴

，
∴，
∴的度数为．
故答案为：．

【点睛】本题考查平行线的性质，三角形的内角和定理，求一个角的补角等知识．正确理解和运用平行线的性质是解题的关键．
7．如图，已知，∠A＝40°，∠C＝65°，则∠P的度数为 _____．

【答案】25°##25度
【分析】根据平行线的性质得出∠PEB=∠C，利用三角形外角的性质，求出∠P的度数即可．
【详解】解：∵，
∴，
∵，
∴．
故答案为：25°．

【点睛】本题主要考查了平行线的性质和三角形外角的性质，熟练掌握两直线平行同位角相等，是解题的关键．
8．欢欢观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知，，，则的度数是________度．

【答案】20
【分析】延长DC交AE于点F，根据平行线的性质求出∠BAE=∠DFE=，利用外角的性质求出∠E=∠DCE-∠DFE=-=即可．
【详解】延长DC交AE于点F，
∵ABDC，
∴∠BAE=∠DFE=，
∵∠DCE=，
∴∠E=∠DCE-∠DFE=-=，
故答案为20．

【点睛】此题考查了平行线的性质：两直线平行同位角相等，以及三角形外角的性质，熟记平行线的性质是解题的关键．
9．如图，若，则∠1+∠3-∠2的度数为______

【答案】180°
【分析】延长EA交CD于点F，则有∠2+∠EFC=∠3，然后根据可得∠1=∠EFD，最后根据领补角及等量代换可求解．
【详解】解：延长EA交CD于点F，如图所示：

，
∠1=∠EFD，
∠2+∠EFC=∠3，
，
，
；
故答案为180°．
【点睛】本题主要考查三角形外角的性质及平行线的性质，熟练掌握三角形外角的性质及平行线的性质是解题的关键．
【提高测试】
1．①如图1，，则；②如图2，，则；③如图3，，则；④如图4，直线 EF，点在直线上，则．以上结论正确的个数是（    ）

A．1个 B．2个 C．3个 D．4个
【答案】B
【分析】①过点E作直线EFAB，由平行线的性质：两直线平行，同旁内角互补，即可得出结论；
②如图2，先根据三角形外角的性质得出∠1＝∠C+∠P，再根据两直线平行，内错角相等即可作出判断；
③如图3，过点E作直线EF∥AB，由平行线的性质可得出∠A+∠AEC﹣∠1＝180°，即得∠AEC＝180°+∠1﹣∠A；
④如图4，根据平行线的性质得出∠α＝∠BOF，∠γ+∠COF＝180°，再利用角的关系解答即可．
【详解】解：

①如图1，过点E作直线EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠A+∠1＝180°，∠2+∠C＝180°，
∴∠A+∠B+∠AEC＝360°，
故①错误；
②如图2，∵∠1是△CEP的外角，
∴∠1＝∠C+∠P，
∵AB∥CD，
∴∠A＝∠1，
即∠P＝∠A﹣∠C，
故②正确；
③如图3，过点E作直线EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠A+∠3＝180°，∠1＝∠2，
∴∠A+∠AEC﹣∠1＝180°，
即∠AEC＝180°+∠1﹣∠A，
故③错误；
④如图4，∵AB∥EF，
∴∠α＝∠BOF，
∵CD∥EF，
∴∠γ+∠COF＝180°，
∵∠BOF＝∠COF+∠β，
∴∠COF＝∠α﹣∠β，
∴∠γ+∠α﹣∠β＝180°，
故④正确；
综上结论正确的个数为2，
故选：B．
【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．
2．①如图1，ABCD，则∠A＋∠E＋∠C＝180°；②如图2，ABCD，则∠E＝∠A＋∠C；③如图3，ABCD，则∠A＋∠E－∠1＝180°；④如图4，ABCD，则∠A＝∠C＋∠P．以上结论正确的个数是（　　）

A．①②③④ B．①②③ C．②③④ D．①②④
【答案】C
【分析】①过点E作直线，由平行线的性质即可得出结论；
②过点E作直线，由平行线的性质即可得出结论；
③过点E作直线，由平行线的性质可得出∠A+∠E-∠1=180°；
④先过点P作直线，再根据两直线平行，内错角相等和同位角相等即可作出判断．
【详解】解：①过点E作直线，

∵，∴，∴∠A＋∠1＝180°，∠2＋∠C＝180°，
∴∠A＋∠C＋∠AEC＝360°，故①错误；
②过点E作直线，

∵，
∴，∴∠A＝∠1，∠2＝∠C，
∴∠AEC＝∠A＋∠C，即∠AEC＝∠A＋∠C，故②正确；
③过点E作直线，

∵，∴，∴∠A＋∠3＝180°，∠1＝∠2，
∴∠A＋∠AEC－∠2＝180°，即∠A＋∠AEC－∠1＝180°，故③正确；
④如图，过点P作直线，

∵，∴，
∴∠1=∠FPA，∠C=∠FPC，
∵∠FPA=∠FPC+∠CPA，
∴∠1＝∠C＋∠CPA，
∵AB∥CD，∴∠A＝∠1，即∠A＝∠C+∠CPA，故④正确．
综上所述，正确的小题有②③④．
故选：C．
【点睛】本题考查的是平行线的性质及平行公理的推论，根据题意作出辅助线是解答此题的关键．
3．如图，AB∥CD，BF,DF 分别平分∠ABE 和∠CDE，BF∥DE，∠F 与∠ABE 互补，则∠F 的度数为

A．30° B．35° C．36° D．45°
【答案】C
【分析】延长BG交CD于G,然后运用平行的性质和角平分线的定义，进行解答即可.
【详解】解：如图延长BG交CD于G

∵BF∥ED
∴∠F=∠EDF
又∵DF 平分∠CDE，
∴∠CDE=2∠F，
∵BF∥ED
∴∠CGF=∠EDF=2∠F，
∵AB∥CD
∴∠ABF=∠CGF=2∠F，
∵BF平分∠ABE
∴∠ABE=2∠ABF=4∠F，
又∵∠F 与∠ABE 互补
∴∠F +∠ABE =180°即5∠F=180°，解得∠F=36°
故答案选C.
【点睛】本题考查了平行的性质和角平分线的定义，做出辅助线是解答本题的关键.
4．如图，则与的数量关系是(   )

A． B．
C． D．
【答案】D
【分析】先设角，利用平行线的性质表示出待求角，再利用整体思想即可求解．
【详解】设
则
∵
∴






∴

故选：D．
【点睛】本题考查了平行线的性质，关键是熟练掌握平行线的性质，注意整体思想的运用．
5．如图，已知直线、被直线所截，，E是平面内任意一点（点E不在直线、、上），设，．下列各式：①，②，③，④，的度数可能是（　　）

A．②③ B．①④ C．①③④ D．①②③④
【答案】D
【分析】由题意根据点E有6种可能位置，分情况进行讨论，依据平行线的性质以及三角形外角性质进行计算求解即可．
【详解】解：（1）如图1，由AB∥CD，可得∠AOC=∠DCE1=β，
∵∠AOC=∠BAE1+∠AE1C，
∴∠AE1C=β-α．

（2）如图2，过E2作AB平行线，则由AB∥CD，可得∠1=∠BAE2=α，∠2=∠DCE2=β，
∴∠AE2C=α+β．

（3）如图3，由AB∥CD，可得∠BOE3=∠DCE3=β，
∵∠BAE3=∠BOE3+∠AE3C，
∴∠AE3C=α-β．

（4）如图4，由AB∥CD，可得∠BAE4+∠AE4C+∠DCE4=360°，
∴∠AE4C=360°-α-β．

（5）（6）当点E在CD的下方时，同理可得∠AEC=α-β或β-α．
综上所述，∠AEC的度数可能为β-α，α+β，α-β，360°-α-β，即①②③④．
故选：D．
【点睛】本题主要考查平行线的性质的运用，解题时注意两直线平行，同位角相等；两直线平行，内错角相等以及分类讨论．
6．请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题.
小明:老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型一“猪蹄模型”.即

已知:如图1，，为、之间一点，连接， 得到.

求证:
小明笔记上写出的证明过程如下:
证明:过点作，
∴
∵，
∴
∴.
∵
∴
请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题.
（1）如图，若，，则___________.

（2）如图，，平分，平分，，则___________.

【答案】     240°     51°
【分析】（1）作EM∥AB，FN∥CD，如图，根据平行线的性质得AB∥EM∥FN∥CD，所以∠B=∠1，∠2=∠3，∠4+∠C=180°，然后利用等量代换计算∠B+∠F+∠C；
（2）分别过G、H作AB的平行线MN和RS，根据平行线的性质和角平分线的性质可用∠ABG和∠DCG分别表示出∠H和∠G，从而可找到∠H和∠G的关系，结合条件可求得∠H．
【详解】（1）解：作EM∥AB，FN∥CD，如图，

AB∥CD，
∴AB∥EM∥FN∥CD，
∴∠B=∠1，∠2=∠3，∠4+∠C=180°，
∴∠B+∠CFE+∠C=∠1+∠3+∠4+∠C=∠BEF+∠4+∠C=∠BEF +180°，
∵，
∴∠B+∠CFE+∠C=60°+180°=240°；
（2）解：如图，分别过G、H作AB的平行线MN和RS，

∵平分，平分，
∴∠ABE=∠ABG，∠SHC=∠DCF=∠DCG，
∵AB∥CD，
∴AB∥CD∥RS∥MN，
∴∠RHB=∠ABE=∠ABG，∠SHC=∠DCF=∠DCG，∠NGB+∠ABG=∠MGC+∠DCG=180°，
∴∠BHC=180°-∠RHB-∠SHC=180°-(∠ABG+∠DCG)，
∠BGC=180°-∠NGB-∠MGC=180°-(180°-∠ABG)-(180°-∠DCG)=∠ABG+∠DCG-180°，
∴∠BGC=360°-2∠BHC-180°=180°-2∠BHC，
又∵∠BGC=∠BHC+27°，
∴180°-2∠BHC=∠BHC+27°，
∴∠BHC =51°．
故答案为：（1）240°；（2）51°．
【点睛】本题考查了平行线的性质和判定的应用，能运用平行线的性质和判定进行推理是解此题的关键，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．
7．已知直线AB∥CD，P为平面内一点，连接PA、PD．
（1）如图1，已知∠A＝50°，∠D＝150°，求∠APD的度数；
（2）如图2，判断∠PAB、∠CDP、∠APD之间的数量关系为 　 　．
（3）如图3，在（2）的条件下，AP⊥PD，DN平分∠PDC，若∠PAN+∠PAB＝∠APD，求∠AND的度数．

【答案】（1）∠APD=80°；（2）∠PAB+∠CDP-∠APD=180°；（3）∠AND=45°．
【分析】（1）首先过点P作PQ∥AB，则易得AB∥PQ∥CD，然后由两直线平行，同旁内角互补以及内错角相等，即可求解；
（2）作PQ∥AB，易得AB∥PQ∥CD，根据平行线的性质，即可证得∠PAB+∠CDP-∠APD=180°；
（3）先证明∠NOD=∠PAB，∠ODN=∠PDC，利用（2）的结论即可求解．
【详解】解：（1）∵∠A=50°，∠D=150°，
过点P作PQ∥AB，

∴∠A=∠APQ=50°，
∵AB∥CD，
∴PQ∥CD，
∴∠D+∠DPQ=180°，则∠DPQ=180°-150°=30°，
∴∠APD=∠APQ+∠DPQ=50°+30°=80°；
（2）∠PAB+∠CDP-∠APD=180°，
如图，作PQ∥AB，

∴∠PAB=∠APQ，
∵AB∥CD，
∴PQ∥CD，
∴∠CDP+∠DPQ=180°，即∠DPQ=180°-∠CDP，
∵∠APD=∠APQ-∠DPQ，
∴∠APD=∠PAB-(180°-∠CDP)=∠PAB+∠CDP-180°；
∴∠PAB+∠CDP-∠APD=180°；
(3)设PD交AN于O，如图，

∵AP⊥PD，
∴∠APO=90°，
由题知∠PAN+∠PAB=∠APD，即∠PAN+∠PAB=90°，
又∵∠POA+∠PAN=180°-∠APO=90°，
∴∠POA=∠PAB，
∵∠POA=∠NOD，
∴∠NOD=∠PAB，
∵DN平分∠PDC，
∴∠ODN=∠PDC，
∴∠AND=180°-∠NOD-∠ODN=180°-(∠PAB+∠PDC)，
由(2)得∠PAB+∠CDP-∠APD=180°，
∴∠PAB+∠PDC=180°+∠APD，
∴∠AND=180°-(∠PAB+∠PDC)
=180°-(180°+∠APD)
=180°-(180°+90°)
=45°，
即∠AND=45°．
【点睛】本题考查了平行线的性质以及角平分线的定义．注意掌握辅助线的作法，注意掌握数形结合思想的应用．
8．（1）如图，AB//CD，CF平分∠DCE，若∠DCF=30°，∠E=20°，求∠ABE的度数；

（2）如图，AB//CD，∠EBF=2∠ABF，CF平分∠DCE，若∠F的2倍与∠E的补角的和为190°，求∠ABE的度数．

（3）如图，P为（2）中射线BE上一点，G是CD上任一点，PQ平分∠BPG，GN//PQ，GM平分∠DGP，若∠B＝30°，求∠MGN的度数．

【答案】（1）∠ABE=40°；（2）∠ABE=30°；（3）∠MGN=15°．
【分析】（1）过E作EMAB，根据平行线的判定与性质和角平分线的定义解答即可；
（2）过E作EMAB，过F作FNAB，根据平行线的判定与性质，角平分线的定义以及解一元一次方程解答即可；
（3）过P作PLAB，根据平行线的判定与性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义解答即可．
【详解】解：（1）过E作EMAB，

∵ABCD，
∴CDEMAB，
∴∠ABE＝∠BEM，∠DCE＝∠CEM，
∵CF平分∠DCE，
∴∠DCE＝2∠DCF，
∵∠DCF＝30°，
∴∠DCE＝60°，
∴∠CEM＝60°，
又∵∠CEB＝20°，
∴∠BEM＝∠CEM﹣∠CEB＝40°，
∴∠ABE＝40°；
（2）过E作EMAB，过F作FNAB，

∵∠EBF＝2∠ABF，
∴设∠ABF＝x，∠EBF＝2x，则∠ABE＝3x，
∵CF平分∠DCE，
∴设∠DCF＝∠ECF＝y，则∠DCE＝2y，
∵ABCD，
∴EMABCD，
∴∠DCE＝∠CEM＝2y，∠BEM＝∠ABE＝3x，
∴∠CEB＝∠CEM﹣∠BEM＝2y﹣3x，
同理∠CFB＝y﹣x，
∵2∠CFB+（180°﹣∠CEB）＝190°，
∴2（y﹣x）+180°﹣（2y﹣3x）＝190°，  
∴x＝10°，
∴∠ABE＝3x＝30°；
（3）过P作PLAB，

∵GM平分∠DGP，
∴设∠DGM＝∠PGM＝y，则∠DGP＝2y，
∵PQ平分∠BPG，
∴设∠BPQ＝∠GPQ＝x，则∠BPG＝2x，
∵PQGN，
∴∠PGN＝∠GPQ＝x，
∵ABCD，
∴PLABCD，  
∴∠GPL＝∠DGP＝2y，
∠BPL＝∠ABP＝30°，
∵∠BPL＝∠GPL﹣∠BPG，
∴30°＝2y﹣2x，
∴y﹣x＝15°，
∵∠MGN＝∠PGM﹣∠PGN＝y﹣x，
∴∠MGN＝15°．
【点睛】此题考查平行线的判定与性质，角平分线的定义，三角形的内角和定理，解题关键在于作辅助线和掌握判定定理．
9．已知直线，直线EF分别与直线a，b相交于点E，F，点A，B分别在直线a，b上，且在直线EF的左侧，点P是直线EF上一动点（不与点E，F重合），设∠PAE＝∠1，∠APB＝∠2，∠PBF＝∠3．

(1)如图，当点在线段上运动时，试说明∠1＋∠3＝∠2；
(2)当点P在线段EF外运动时有两种情况．
①如图2写出∠1，∠2，∠3之间的关系并给出证明；
②如图3所示，猜想∠1，∠2，∠3之间的关系（不要求证明）．
【答案】(1)证明见详解
(2)①；证明见详解；②；证明见详解

【分析】（1）如图4过点作，利用平行线的传递性可知，根据平行线的性质可知，，根据等量代换就可以得出；
（2）①如图5过点作，利用平行线的传递性可知，根据平行线的性质可知，，根据等量代换就可以得出；
②如图6过点作，利用平行线的传递性可知，根据平行线的性质可知，，根据等量代换就可以得出．
（1）
解：如图4所示：过点作，
∵
∴
∴，，
∵，
∴；

（2）
解：①如图5过点作，
∵
∴
∴，，
∵，
∴；

②如图6过点作，
∵
∴
∴，，
∵，
∴．

【点睛】本题利用“猪蹄模型”及其变式考查了利用平行线的性质求角之间的数量关系，准确的作出辅助线和找到对应的内错角是解决本题的关键．
10．请你探究：如图（1），木杆与平行，木杆的两端、用一橡皮筋连接．

（1）在图（1）中，与有何关系？
（2）若将橡皮筋拉成图（2）的形状，则、、之间有何关系？
（3）若将橡皮筋拉成图（3）的形状，则、、之间有何关系？
（4）若将橡皮筋拉成图（4）的形状，则、、之间有何关系？
（5）若将橡皮筋拉成图（5）的形状，则、、之间有何关系？
（注：以上各问，只写出探究结果，不用说明理由）
【答案】（1）∠B+∠C=180º；（2）∠B+∠C=∠A；（3）∠A +∠B+∠C=360º；（4）∠A+∠B=∠C；（5）∠A+∠C =∠B
【分析】（1）利用平行线的性质“两直线平行，同旁内角相等”即可解答；
（2）过点A作AD∥BE，利用“两直线平行，内错角相等”即可得出结论；
（3）同样过点A作AD∥BE，利用“两直线平行，同旁内角互补”即可得出结论；
（4）利用“两直线平行，同位角相等”和三角形外角性质可得出结论；
（5）利用“两直线平行，同位角相等”和三角形外角性质可得出结论．
【详解】（1）如图（1）∵与平行，∴∠B+∠C=180º；
（2）如图（2），过点A作AD∥BE，则AD∥BE∥CF（平行于同一条直线的两条直线平行），
∴∠B=∠BAD，∠C=∠DAC，
∴∠B+∠C=∠BAD+∠DAC=∠BAC，
即∠B+∠C=∠A；
（3）如图（3），过点A作AD∥BE，则AD∥BE∥CF，
∴∠B+∠BAD=180º，∠DAC+∠C=180º，
∴∠B+∠BAD+∠DAC+∠C=360º，
即∠B+∠A+∠C=360º；
（4）如图（4），设BE与AC相交于D，
∵与平行，
∴∠C=∠ADE，
∵∠ADE=∠A+∠B，
∴∠A+∠B=∠C；
（5）如图（5），设CF与AB相交于D，
∵与平行，
∴∠B=∠ADF，
∵∠ADF=∠A+∠C，
∴∠A+∠C=∠B．

【点睛】本题考查了平行线的性质、三角形的外角性质，熟练掌握平行线的性质，作辅助平行线是解答的关键．
11．如图，已知，求证：.

【答案】见解析.
【分析】作PQ∥BE，由平行线的性质和判定可求证BE∥FC，然后再由邻补角的定义、三角形外角的性质及平行线的性质可求证∠A+∠B+∠C+∠D=180°.
【详解】解：作PQ∥BE，如图所示：

∵BE∥PQ，
∴∠1=∠EOP，
∵∠3=∠1+∠2，∠3=∠EOP+∠POF，
∴∠2=∠POF，
∴PQ∥FC，
∴BE∥FC，
∴∠AME=∠FNA，
又∵∠AME=∠A+∠B,∠FND=∠C+∠D,∠FNA+∠FND=180°，
∴∠A+∠B+∠C+∠D=180°.
【点睛】本题主要考查了平行线的判定和性质、三角形的外角和定理、邻补角的定义等知识点，根据题意和所学知识证明BE∥FC是解题的关键.
12．如图所示，，，，求的度数.

【答案】.
【分析】根据平行线的性质，由靴子图ABEFC知，，，由靴子图知，，
又因为，得到，所以.
【详解】因为，结合题意，由靴子图ABEFC知，，，由靴子图知，，
，
即，
，
【点睛】本题考查平行线的性质，解题的关键是熟练掌握平行线的性质.
13．已知，AB∥DE，点C在AB上方，连接BC、CD．
（1）如图1，求证：∠BCD＋∠CDE＝∠ABC；
（2）如图2，过点C作CF⊥BC交ED的延长线于点F，探究∠ABC和∠F之间的数量关系；
（3）如图3，在（2）的条件下，∠CFD的平分线交CD于点G，连接GB并延长至点H，若BH平分∠ABC，求∠BGD﹣∠CGF的值．

【答案】（1）证明见解析；（2）；（3）．
【分析】（1）过点作，先根据平行线的性质可得，再根据平行公理推论可得，然后根据平行线的性质可得，由此即可得证；
（2）过点作，同（1）的方法，先根据平行线的性质得出，，从而可得，再根据垂直的定义可得，由此即可得出结论；
（3）过点作，延长至点，先根据平行线的性质可得，，从而可得，再根据角平分线的定义、结合（2）的结论可得，然后根据角的和差、对顶角相等可得，由此即可得出答案．
【详解】证明：（1）如图，过点作，

，
，
，
，即，
，
；
（2）如图，过点作，

，
，
，
，即，
，
，
，
，
；
（3）如图，过点作，延长至点，

，
，
，
，
平分，平分，
，
由（2）可知，，
，
又，
．
【点睛】本题考查了平行线的性质、对顶角相等、角平分线的定义等知识点，熟练掌握平行线的性质是解题关键．