专题02 最短路径问题2（解析版）

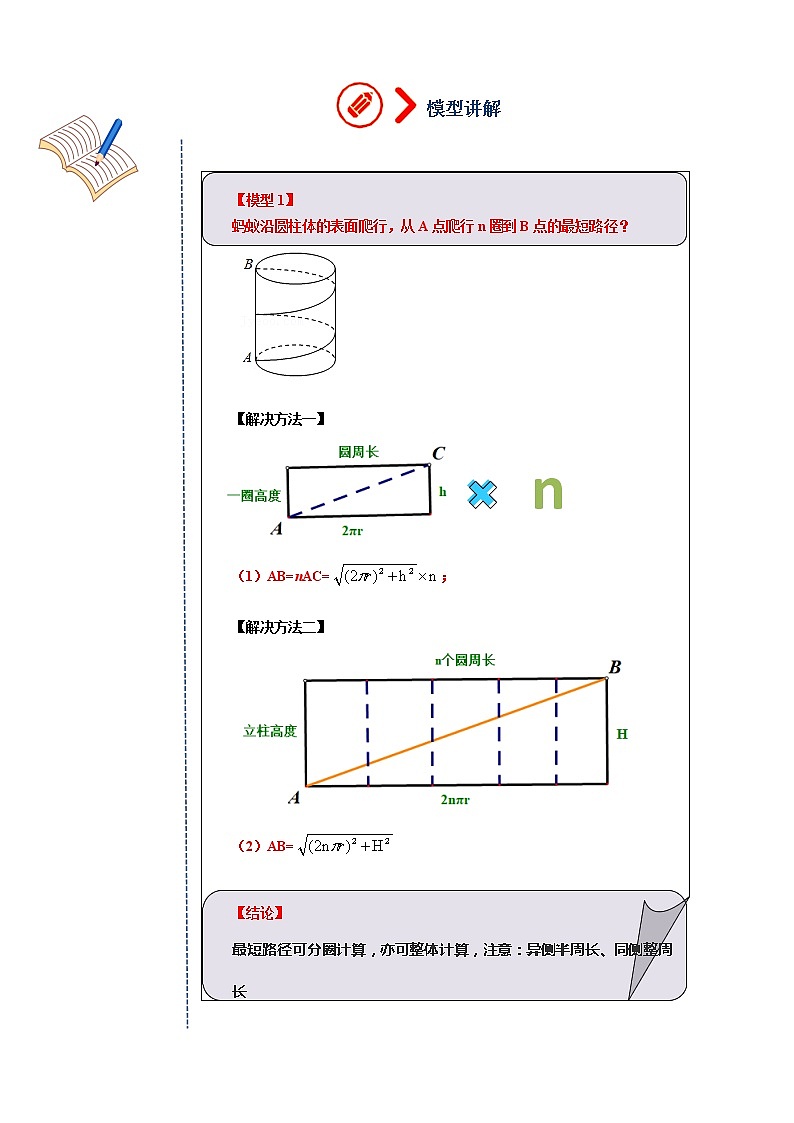
【模型1】

蚂蚁沿圆柱体的表面爬行，从A点爬行n圈到B点的最短路径？

【解决方法一】

（1）AB=nAC=；

【解决方法二】

（2）AB=

【结论】

最短路径可分圈计算，亦可整体计算，注意：异侧半周长、同侧整周长

【模型2】

蚂蚁吃蜂蜜问题：蚂蚁从圆柱体的外壁A处爬行到内壁B处的最短路径？

【路径演示】

由图可知蚂蚁爬行的最短路径A’B=

方法点拨

一、解决方法：

①确定水平方向移动路程②确定竖直方向移动路程

③利用勾股定理求解

二、方法解析：

。

1．．如图所示，在正三棱柱ABC一A1B1C1中，已知AB＝BC＝CA＝2，AA1＝4，一只蚂蚁从A点出发绕三棱柱侧面两圈到达点A1，则蚂蚁爬行的最短距离为（　　）

A． B．2+2 C．4 D．4

【解答】解：如图，把侧面展开两周，矩形对角线即为蚂蚁爬行的最短距离，

蚂蚁爬行的最短距离＝＝4，

故选：D．

2．如图，圆柱形玻璃杯高为11cm，底面周长为30cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的爬行最短路线长为（杯壁厚度不计）（　　）

A．12cm B．17cm C．20cm D．25cm

【解答】解：如图：

将杯子侧面展开，

作A关于EF的对称点A′，

则AF+BF为蚂蚁从外壁A处到内壁B处的最短距离，即A′B的长度，

∵A′B＝＝＝＝17（cm），

∴蚂蚁从外壁A处到内壁B处的最短距离为17cm，

故选：B．

3．如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连接AC，EC．已知AB＝4，DE＝2，BD＝8，设CD＝x．

（1）用含x的代数式表示AC+CE的长．

（2）观察图形，请问在什么情况下，AC+CE的值最小？最小值多少？写出计算过程．

（3）求代数式+的最小值．

【解答】解：（1）AC+CE＝；

（2）当A、C、E三点共线时，AC+CE的值最小，

过A点作AF平行于BD交ED的延长线于点F，得矩形ABDF，

则DF＝AB＝4，AF＝BD＝8，EF＝ED+DF＝2+4＝6，

所以，

则AC+CE的最小值为10；

（3）构造图形作BD＝4，分别过点B，D作AB⊥BD，ED⊥BD，AB＝2，DE＝1，

C为线段BD上一动点，设BC＝x，

当A、C、E三点共线时，AE的长即为代数式的最小值．

过A点作AF平行于BD交ED的延长线于点F，得矩形ABDF．

则DF＝AB＝2，AF＝BD＝4，EF＝ED+DF＝1+2＝3，

所以，

过A点作AF平行于BD交ED的延长线于点F，得矩形ABDF．则DF＝AB＝4，AF＝BD＝8，EF＝ED+DF＝2+4＝6BF，

则AC+CE的最小值为5．

1．如图，一个圆柱形工艺品高为18厘米，底面周长12厘米．现在需要从下底的A处绕侧面两周，到上底B（A的正上方）处镶嵌一条金丝，则金丝至少　30　厘米．

【解答】解：如图，设AB的中点为M，侧面展开图是ABCD，CD的中点是N，

则金丝的最小值为侧面展开图中的AN+MC，

∵AN＝MC＝＝15（厘米），

∴金丝至少15×2＝30厘米．

故答案为：30．

2．如图．长方体的底面是边长2cm的正方形，高为6cm．如果从点A开始经过4个侧面缠绕2圈到达B，那么所用细线最短需要　2　cm．

【解答】解：将长方体的侧面沿AB展开，取A′B′的中点C，取AB的中点C′，连接B′C′，AC，则AC+B′C′为所求的最短细线长，

∵AC2＝AA′2+A′C2，AC＝cm，

∴B′C′2＝BB′2+C′B2＝73，

∴B′C′＝（cm），

∴AC+B′C′＝2（cm），

答：所用细线最短长度是2cm，

故答案为：2．

3．如图，小冰想用一条彩带缠绕圆柱4圈，正好从A点绕到正上方的B点，已知圆柱底面周长是3m，高为5m，则所需彩带最短是　13　m．

【解答】解：如图，将这个圆柱体侧面展开得，

由勾股定理得，

AC＝＝13，

故答案为：13．

4．如图，透明的圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离容器底部2cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿2cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是（　　）

A．13cm B．cm C．cm D．cm

【解答】解：如图：

∵高为12cm，底面周长为10cm，在容器内壁离容器底部2cm的点B处有一饭粒，

此时蚂蚁正好在容器外壁，离容器上沿2cm与饭粒相对的点A处，

∴A′D＝5cm，BD＝12﹣2+AE＝12cm，

∴将容器侧面展开，作A关于EF的对称点A′，

连接A′B，则A′B即为最短距离，

A′B＝＝＝13（cm），

故选：A．

5．如图，透明的圆柱形玻璃容器（容器厚度忽略不计）的高为16cm，在容器内壁离容器底部4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，位于离容器上沿4cm的点A处，若蚂蚁吃到蜂蜜需爬行的最短路径为20cm，则该圆柱底面周长为（　　）

A．12cm B．14cm C．20cm D．24cm

【解答】解：如图：将圆柱展开，EG为上底面圆周长的一半，

作A关于E的对称点A'，连接A'B交EG于F，则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF的长，即AF+BF＝A'B＝20cm，

延长BG，过A'作A'D⊥BG于D，

∵AE＝A'E＝DG＝4cm，

∴BD＝16cm，

Rt△A'DB中，由勾股定理得：A'D＝＝12cm，

∴则该圆柱底面周长为24cm．

故选：D．

6．如图，A，B是笔直公路l同侧的两个村庄，且两个村庄到公路的距离分别是300m和500m，两村庄之间的距离为d（已知d2＝400000m2），现要在公路上建一汽车停靠站，使两村到停靠站的距离之和最小，问最小值是多少？

【解答】解：作点B关于公路l的对称点B′，连接AB′交公路于点C，

此时满足停靠站到两村之和距离最小，此时的距离之和＝CA+CB＝CA+CB'＝AB'，

作AD⊥BB'于点D，则CB+CA＝CB'+CA＝AB'，

由题意得，AB2＝d2＝400000m2，DB＝BE﹣DE＝BE﹣AF＝200m，DB'＝DE+EB'＝800m，

在RT△ADB中，AD2＝AB2﹣BD2＝400000﹣40000＝360000，

在RT△ADB'中，AB'＝＝1000米．

答：停靠站建在点C出使得两村到停靠站的距离之和最小，最小值为1000米．

7．如图，笔直的公路上有A、B两个站点相距40km，在公路的同侧有C、D两个村庄，DA⊥AB，CB⊥AB，且DA＝20km，CB＝10km，现政府决定在A、B之间建一个土特产加工基地E．

（1）若要使土特产加工基地E点到C、D两村的距离相等，请用直尺和圆规在图1中作出点E；

（2）在（1）的条件下求出基地E到A站的距离；

（3）若要使土特产加工基地E点到C、D两村的距离和（即DE+EC）最小，求出此最小的距离和．

【解答】解：（1）如图，点E即为所求．

（2）∵点E为线段CD的垂直平分线的交点，

∴DE＝CE，

∵DA⊥AB，CB⊥AB，

∴∠A＝∠B＝90°，

∴AD2+AE2＝CB2+BE2，

∴202+AE2＝（40﹣AE）2+102，

∴AE＝＝（km）．

（3）作点D关于AB的对称点D’，连接C，D’交AB于点E，（DE+CE）的最小值即为（D’E+EC）的值，

作CF⊥AD于F．

在Rt△CFD′中，CD′＝＝＝50（km）

∴最小距离为50km．

8．数与形是数学中的两个最古老，也是最基本的研究对象，它们在一定条件下可以相互转化，数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的．

（1）【思想应用】已知m，n均为正实数，且m+n＝2，求的最小值．通过分析，爱思考的小明想到了利用下面的构造解决此问题：如图，AB＝2，AC＝1，BD＝2，AC⊥AB，BD⊥AB，点E是线段AB上的动点，且不与端点重合，连接CE，DE，设AE＝m，BE＝n，

①用含m的代数式表示CE＝　　，用含n的代数式表示DE＝　　；

②据此求的最小值；

（2）【类比应用】根据上述的方法，代数式的最小值是　20　．

【解答】解：（1）①在Rt△ACE中，CE＝，

在Rt△BDE中，DE＝＝；

②＝CE+DE，

而CE+DE≥CD（当且仅当C、E、D共线时取等号），

作DH⊥CA交CA的延长线于H，如图，易得四边形ABDH为矩形，

∴AH＝BD＝2，DH＝AB＝2，

在Rt△CHD中，CD＝＝，

∴CE+DE的最小值为，

即的最小值为；

（2）如图，设AB＝16，CA＝5，BD＝7，AE＝x，则BE＝16﹣x，

在Rt△ACE中，CE＝＝，

在Rt△BDE中，DE＝＝；

＝CE+DE，

而CE+DE≥CD（当且仅当C、E、D共线时取等号），

作DH⊥CA交CA的延长线于H，如图，易得四边形ABDH为矩形，

∴AH＝BD＝7，DH＝AB＝16，

在Rt△CHD中，CD＝＝20，

∴CE+DE的最小值为20，

即的最小值为20．

故答案为，+；20．

9．如图，在平面直角坐标系中，点A（a，0），AB⊥x轴，且AB＝10，点C（0，b），a，b满足b＝++15．点P（t，0）是线段AO上一点（不包含A，O）．

（1）当t＝5时，求PB：PC的值；

（2）当PC+PB最小时，求t的值；

（3）请根据以上的启发，解决如下问题：正数m，n满足m+n＝10，且正数p＝+，则正数p的最小值＝　2　．

【解答】解：（1）依题意，得，

，

解得，a＝25，

∴b＝15，

∴A（25，0），C（0，15），

∵AB⊥x且AB＝10，

∴B（25，10），

当t＝5时，P（5，0），

∴PB＝，

pc＝，

∴PB：PC＝：1．

（2）如图，作点B关于x轴的对称点B′，连接CB′交x轴于点P，

根据两点之间，线段最短可得此时，

PC+PB＝PC+PB′＝CB′的值最小，

设直线CB′的解析式为y＝kx+15，

∵B（25，10）关于x轴的对称点为B′（25，﹣10），

∴25k+15＝﹣10，

∴k＝﹣1，

∴y＝﹣x+15，

把y＝0代入得，x＝15，

∴t＝15；

（3）依题意，得n＝10﹣m，

∴p＝+，

即求（m，0）到（0，3）和到（10，5）的距离和的最小值，

由（2）可知（10，5）关于x轴对称点为（10，﹣5），

∴p＝．

故答案为：2．

（2007•义乌市）李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题，请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长．

（1）如图1，正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处；

（2）如图2，正四棱柱的底面边长为5cm，侧棱长为6cm，一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处；

（3）如图3，圆锥的母线长为4cm，圆锥的侧面展开图如图4所示，且∠AOA1＝120°，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A．

【解答】解：

（1）（cm）；

（2）画图分两种情况：

①当横向剪开时：（cm），

②当竖向剪开时：（cm）；

∵，∴最短路程为cm．

（3）如图所示：

连接AA1，过点O作OD⊥AA1于点D，

在Rt△ADO和Rt△A1DO中，

∵OA＝OA1，

∴AD＝A1D，∠AOD＝∠AOA1＝60°，

∴AD＝OAsin60°＝4×＝2（cm），

∴AA1＝2AD＝4（cm），

∴所求的最短的路程为AA1＝cm．