专题05 费马点模型（解析版）

这是一份专题05 费马点模型（解析版），共26页。























费马点模型






模型讲解



费马点：三角形内的点到三个顶点距离之和最小的点
【结论】
如图，点M为锐角△ABC内任意一点，连接AM、BM、CM，当M与三个顶点连线的夹角为120°时，MA+MB+MC的值最小


【证明】以AB为一边向外作等边三角形△ABE，将BM绕点B逆时针旋转60°得到BN，连接EN．
∵△ABE为等边三角形，
∴AB＝BE，∠ABE＝60°．
而∠MBN＝60°，
∴∠ABM＝∠EBN．
在△AMB与△ENB中，
∵，
∴△AMB≌△ENB（SAS）．
连接MN．由△AMB≌△ENB知，AM＝EN．
∵∠MBN＝60°，BM＝BN，
∴△BMN为等边三角形．
∴BM＝MN．
∴AM+BM+CM＝EN+MN+CM．
∴当E、N、M、C四点共线时，AM+BM+CM的值最小．
此时，∠BMC＝180°﹣∠NMB＝120°；
∠AMB＝∠ENB＝180°﹣∠BNM＝120°；
∠AMC＝360°﹣∠BMC﹣∠AMB＝120°．


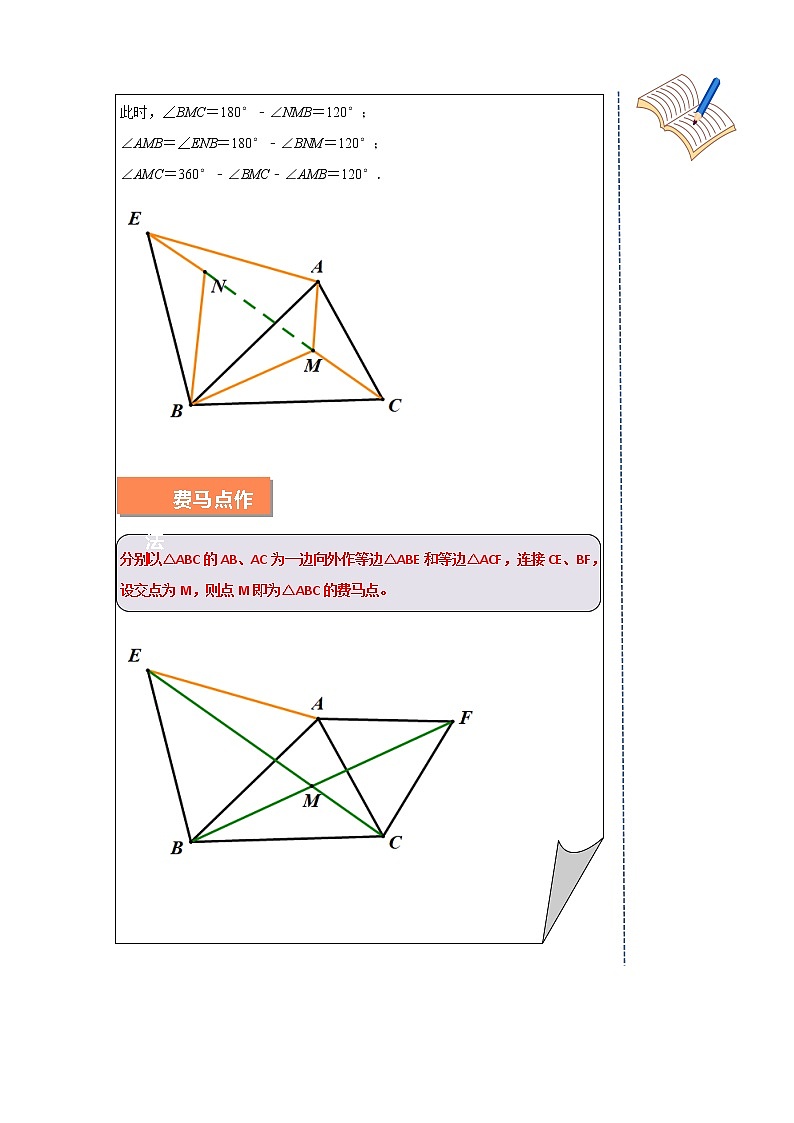
费马点作法




分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF，连接CE、BF，设交点为M，则点M即为△ABC的费马点。









加权费马点


点P为锐角△ABC内任意一点，连接AP、BP、CP，求xAP+yBP+zCP最小值

解决办法：
第一步，选定固定不变线段；
第二步，对剩余线段进行缩小或者放大。
如：保持BP不变，xAP+yBP+zCP=，如图所示，B、P、P2、A2四点共线时，取得最小值。

例：点P为锐角△ABC内任意一点，∠ACB=30°，BC=6，AC=5，连接AP、BP、CP，求3AP+4BP+5CP的最小值
【分析】将△APC绕C点顺时针转90°到△A1P1C，过P2作P1A1的平行线，交CA1于点A2，且满足A2P2：P1A1=3：4.
在Rt△PCP2中，设PC=a，由△CA2P2∽△CA1P1得CP2=3a/4，则PP2=5a/4。
∴3AP+4BP+5CP=
∴B、P、P2、A2四点共线时，取得最小值。接触BA2长度即可。










方法点拨
一、题型特征：PA+PB+PC（P为动点）
①一动点，三定点
②以三角形的三边向外作等边三角形的，再分别将所作等边三角形最外的顶点与已知三角形且与所作等边三角形相对的顶点相连，连线的交点即为费马点。
③同时线段前可以有不为1的系数出现，即：加权费马点
二、模型本质：两点之间，线段最短。




例题演练

1．如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．
（1）当M点在何处时，AM+BM+CM的值最小，并说明理由；
（2）当AM+BM+CM的最小值为时，求正方形的边长．

【解答】如图，连接CE，当M点位于BD与CE的交点处时，
AM+BM+CM的值最小，
理由如下：连接MN，由（1）知，△AMB≌△ENB，
∴AM＝EN，
∵∠MBN＝60°，MB＝NB，
∴△BMN是等边三角形．
∴BM＝MN．
∴AM+BM+CM＝EN+MN+CM．
根据“两点之间线段最短”可知，若E、N、M、C在同一条直线上时，EN+MN+CM取得最小值，最小值为EC．
在△ABM和△CBM中，
，
∴△ABM≌△CBM（SAS），
∴∠BAM＝∠BCM，
∴∠BCM＝∠BEN，
∵EB＝CB，
∴若连接EC，则∠BEC＝∠BCE，
∵∠BCM＝∠BCE，∠BEN＝∠BEC，
∴M、N可以同时在直线EC上．
∴当M点位于BD与CE的交点处时，AM+BM+CM的值最小，即等于EC的长．

（2）解：过E点作EF⊥BC交CB的延长线于F，
∴∠EBF＝∠ABF﹣∠ABE＝90°﹣60°＝30°．
设正方形的边长为x，则BF＝x，EF＝．
在Rt△EFC中，
∵EF2+FC2＝EC2，
∴（）2+（x+x）2＝．
解得x1＝，x2＝﹣（舍去负值）．
∴正方形的边长为．


2．已知，如图在△ABC中，∠ACB＝30°，BC＝5，AC＝6，在△ABC内部有一点D，连接DA、DB、DC，则DA+DB+DC的最小值是　　．

【解答】解：如图，过点C作CE⊥CD，且CE＝CD，连接DE，将△ADC绕点C逆时针旋转90°得到△FEC，连接FB，过点F作FH⊥BC，交BC的延长线于H，

∵CE⊥CD，CE＝CD，
∴DE＝CD，
∵将△ADC绕点C逆时针旋转90°得到△FEC，
∴EF＝AD，∠ACF＝90°，CF＝AC＝6，
∴DA+DB+DC＝DB+EF+DE，
∴当点F，点E，点D，点B共线时，DA+DB+DC有最小值为FB，
∵∠FCH＝180°﹣∠ACF﹣∠ACB＝60°，
∴∠CFH＝30°，
∴CH＝CF＝3，FH＝CH＝3，
∴BF＝＝＝，
故答案为：．

强化训练



1．数学上称“费马点”是位于三角形内且到三角形三个顶点距离之和最短的点．现定义：菱形对角线上一点到该对角线同侧两条边上的两点距离最小的点称为类费马点．例如：菱形ABCD，P是对角线BD上一点，E、F是边BC和CD上的两点，若点P满足PE与PF之和最小，则称点P为类费马点．

（1）如图1，在菱形ABCD中，AB＝4，点P是BD上的类费马点
①E为BC的中点，F为CD的中点，则PE+PF＝　 　．
②E为BC上一动点，F为CD上一动点，且∠ABC＝60°，则PE+PF＝　 　．
（2）如图2，在菱形ABCD中，AB＝4，连接AC，点P是△ABC的费马点，（即PA，PB，FC之和最小），①当∠ABC＝60°时，BP＝　 　．
②当∠ABC＝30°时，你能找到△ABC的费马点P吗？画图做简要说明，并求此时PA+PB+PC的值．
【解答】解：（1）①取AB的中点E'，连接PE'，

∵四边形ABCD是菱形，
∴BC＝AB＝CD，∠ABP＝∠CBP，
∵点E，E'分别是AB，BC的中点，
∴BE＝BE'，
在△BEP和△BE'P中，
，
∴△BEP≌△BE'P（SAS），
∴PE＝PE'，
∴PE+PF＝PE'+PF，
∴当E'、P、F三点共线时，PE+PF最小值为E'F的长，
∵AE'＝DF，AE'∥DF，
∴四边形AE'FD是平行四边形，
∴E'F＝AB＝4，
∴PE+PF＝4，
故答案为：4；
②由①知PE+PF＝E'F，若E、F为动点，则E'F的最小值为AB与CD之间的距离，
∴过点C作CH⊥AB于H，

在Rt△BCH中，
sin∠CBH＝，
∴CH＝2，
∵点P是BD上的类费马点
∴PE+PF的最小值为2；
故答案为：2；
（2）①如图2，将△BPC绕点B顺时针旋转60°得△BP'C'，连接PP'，

∴BP＝BP'，PC＝P'C'，∠PBP'＝60°，
∴△BPP'是等边三角形，
∴PP'＝PB，
∴PA+PB+PC＝PA+PP'+P'C'，
∴当P、P'在线段AC'上时，PA+PB+PC最小值为AC'的长，
∴连接AC'，AC'与BD的交点为P点，
∵AB＝BC＝4，∠ABC＝120°，
∴∠BAP＝∠ABP＝30°，AC'＝4，
∴AP＝BP，
同理BP'＝CP'，
∴BP＝AC'＝；
故答案为：；
②如图3，将△BPC绕点B顺时针旋转60°得△BP'C'，连接PP'，

∴BP＝BP'，PC＝P'C'，∠PBP'＝60°，∠CBC'＝60°，
∴△BPP'是等边三角形，
∴PP'＝PB，
∴PA+PB+PC＝PA+PP'+P'C'，
∴当P、P'在线段AC'上时，PA+PB+PC最小值为AC'的长，
且线段AC'在△ABC内部的线段即为费马点P，
∵∠ABC'＝90°，AB＝BC'＝4，
∴AC'＝，
∴此时PA+PB+PC的最小值为4．

2．阅读材料：
平面几何中的费马问题是十七世纪法国数学家、被誉为业余数学家之王的皮埃尔•德•费马提出的一个著名的几何问题．1643年，在一封写给意大利数学家和物理学家托里拆利的私人信件中，费马提出了下面这个极富挑战性和趣味性的几何难题，请求托里拆利帮忙解答：
给定不在一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最短的点P的位置．
托里拆利成功地解决了费马的问题．后来人们就把平面上到一个三角形的三个顶点A，B，C距离之和最小的点称为△ABC的费马﹣托里拆利点，也简称为费马点或托里拆利点．
问题解决：
（1）费马问题有多种不同的解法，最简单快捷的还是几何解法．如图1，我们可以将△BPC绕点B顺时针旋转60°得到△BDE，连接PD，可得△BPD为等边三角形，故PD＝PB，由旋转可得DE＝PC，因此PA+PB+PC＝PA+PD+DE，由 　 　可知，PA+PB+PC的最小值与线段 　 　的长度相等；
（2）如图2，在直角三角形△ABC内部有一动点P，∠BAC＝90°，∠ACB＝30°，连接PA，PB，PC，若AB＝2，求PA+PB+PC的最小值；
（3）如图3，菱形ABCD的边长为4，∠ABC＝60°，平面内有一动点E，在点E运动过程中，始终有∠BEC＝90°，连接AE、DE，在△ADE内部是否存在一点P，使得PA+PD+PE最小，若存在，请直接写出PA+PD+PE的最小值；若不存在，请说明理由．



【解答】解：（1）将△BPC绕点B顺时针旋转60°得到△BDE，连接PD，可得△BPD为等边三角形，故PD＝PB，
由旋转可得DE＝PC，因此PA+PB+PC＝PA+PD+DE，
由两点之间线段最短可知，PA+PB+PC的最小值与线段AE的长度相等．
故答案为：两点之间线段最短，AE．
（2）如图，将△ABP绕点B顺时针旋转60°得到△EBF，连接PF，CE，作EH⊥CA交CA的延长线于H．

在Rt△ABC中，∵∠ABC＝30°，AB＝2，
∴BC＝2AC＝4，AB＝AC＝2，
由旋转的旋转可知：PA＝EF，△PBF，△ABE是等边三角形，
∴PF＝PB，
∴PA+PB+PC＝EF+FP+PC，
∵EF+FP+PC≥CE，
∴当C，P，F，E共线时，PA+PB+PC的值最小，
∵∠BAC＝90°，∠CAE＝60°，
∴∠HAE＝180°﹣90°﹣60°＝30°，
∵EH⊥AH，AE＝AB＝2，
∴EH＝AE＝1，AH＝EH＝，
∴CE＝＝＝2，
∴PA+PB+PC的最小值为2．
故答案为2．

（3）如图3中，将△ADP绕点A逆时针旋转90°得到△TAH，连接PH，DT，CT．

∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD，
∵∠ABC＝60°，
∴△ABC，△ADC都是等边三角形，
∵∠BEC＝90°，
∴点E在以BC为直径的⊙O上运动，
连接OT，OE，则OE＝BC＝2，
由旋转的性质可知，△PAH，△ADT都是等边三角形，PA＝PH，HT＝PD，
∵OE+PE+PH+TH≥OT，
∴PE+PA+PD≥OT﹣OE，
∵TA＝TD＝AC＝CD＝AD＝4，
∴CT⊥AD，
∵AD∥BC，
∴CT⊥BC，CT＝4，
∴OT＝＝2，
∴PE+PA+PD≥2﹣2，
∴PA+PD+PE的最小值为2﹣2．


3．若点P为△ABC所在平面上一点，且∠APB＝∠BPC＝∠CPA＝120°，则点P叫做△ABC的费马点．当三角形的最大角小于120°时，可以证明费马点就是“到三角形的三个顶点的距离之和最小的点”．即PA+PB+PC最小．
（1）如图1，向△ABC外作等边三角形△ABD，△AEC．连接BE，DC相交于点P，连接AP．
①证明：点P就是△ABC费马点；
②证明：PA+PB+PC＝BE＝DC；
（2）如图2，在△MNG中，MN＝4，∠M＝75°，MG＝3．点O是△MNG内一点，则点O到△MNG三个顶点的距离和的最小值是 　 　．

【解答】（1）证明：①如图1﹣1中，作AM⊥CD于M，AN⊥BE于N设AB交 CD于O．

∵△ADB，△ACE都是等边三角形，
∴AD＝AB，AC＝AE，∠DAB＝∠CAE＝60°，
∴∠DAC＝∠BAE，
∴△ADC≌△ABE（SAS），
∴CD＝BE，S△DAC＝S△ABE，∠ADC＝∠ABE，
∵AM⊥CD，AN⊥BE，
∴•CD•AM＝•BE•AN，
∴AM＝AN，
∴∠APM＝∠APN，
∵∠AOD＝∠POB，
∴∠OPB＝∠DAO＝60°，
∴∠APN＝∠APM＝60°，
∴∠APC＝∠BPC＝∠APC＝120°，
∴点P是就是△ABC费马点．

②在线段PD上取一点T，使得PA＝PT，连接AT．

∵∠APT＝60°，PT＝PA，
∴△APT是等边三角形，
∴∠PAT＝60°，AT＝AP，
∵∠DAB＝∠TAP＝60°，
∴∠DAT＝∠BAP，∵AD＝AB，
∴△DAT≌△BAP（SAS），
∴PB＝DT，
∴PD＝DT+PT＝PA+PB，
∴PA+PB+PC＝PD+PC＝CD＝BE．

（2）解：如图2：以MG为边作等边三角形△MGD，以OM为边作等边△OME．连接ND，作DF⊥NM，交NM的延长线于F．

∵△MGD和△OME是等边三角形
∴OE＝OM＝ME，∠DMG＝∠OME＝60°，MG＝MD，
∴∠GMO＝∠DME
在△GMO和△DME中，
，
∴△GMO≌△DME（SAS），
∴OG＝DE
∴NO+GO+MO＝DE+OE+NO
∴当D、E、O、N四点共线时，NO+GO+MO值最小，
∵∠NMG＝75°，∠GMD＝60°，
∴∠NMD＝135°，
∴∠DMF＝45°，
∵MG＝3
∴MF＝DF＝，
∴NF＝MN+MF＝4+＝，
∴ND＝＝＝，
∴MO+NO+GO最小值为，
故答案为，


4．如图，在菱形ABCD中，∠ABC＝60°，点E、F分别是AB、BC上的动点，连接DE、DF、EF．
（1）如图1，连接AF，若AF⊥BC，E为AB的中点，且EF＝2，求DF的长；
（2）如图2，若BE＝BF，G为DE的中点，连接AF、AG、FG，求证：AG⊥FG；
（3）如图3，若AB＝4，将△BEF沿EF翻折得到△EFP（始终保持点P在菱形ABCD的内部），连接AP、BP及CP，请直接写出当PA+PB+PC值最小时PB的长．

【解答】解：（1）方法1、如图1，
∵AF⊥BC，
∴∠AFB＝90°，
∵E为AB的中点，
∴AE＝BE，
∴EF＝BE＝AB＝2，
∵∠ABC＝60°，
∴BF＝EF＝BC，
∴CF＝EF＝2，
过点D作DG⊥BC交BC的延长线于G，
在Rt△CDG中，∠DCG＝180°﹣∠BCD＝60°，
∴∠CDG＝30°，CG＝CD＝2，DG＝CG＝2，
∴FG＝CF+CG＝4，
在Rt△DFG中，DF＝＝2；
方法2、∵AF⊥BC，
∴∠AFB＝90°，
∵点E是AB的中点，
∴AE＝BE，
在Rt△ABF中，EF＝BE＝AB，
∴AB＝4，
∵四边形ABCD是菱形，
∴AD＝AB＝4，∠BAD＝180°﹣∠ABC＝120°，
在Rt△ABF中，∠ABC＝60°，
∴∠BAF＝30°，
∴AF＝2，∠DAF＝∠BAD﹣∠BAF＝90°，
在Rt△ADF中，根据勾股定理得，DF＝＝2；

（2）方法1、如图2，延长AG交CD于H，连接AC，FH，
∵AB∥CD，
∴∠AEG＝∠HDG，
∵G为DE的中点，
∴EG＝DG，
在△AEG和△DHG中，，
∴△AEG≌△DHG，
∴AG＝HG，AE＝DH，
∵AB＝BC＝CD，BE＝BF，
∴FC＝DH，BF＝CH，
在△AFC和△AHD中，，
∴△AFC≌△AHD，
∴AH＝AF，
同理：△ABF≌△ACH，
∴∠BAF＝∠CAH，
∴∠FAH＝∠FAC+∠CAH＝∠FAC+∠BAF＝∠BAC＝60°，
∴△AFH是等边三角形，
∵AG＝HG，
∴AG⊥FG．
方法2、
延长AG交CD于H，连接FH，
∵四边形ABCD是菱形，
∴AB＝CD，AB∥CD，
∴∠EAG＝∠DHG，∠AEG＝∠HDG，
∵点G是DE中点，
∴EG＝DG，
∴△AEG≌△HDG，
∴AG＝HG，AE＝DH，
∴BE＝CH，
∵BE＝BF，∠ABC＝60°，
∴△BEF是等边三角形，
∴∠BEF＝60°，EF＝BE，
∴∠AEF＝∠FCH，EF＝CH，
∴△AEF≌△FCH，
∴AF＝HF，
∵AG＝HG，
∴FG⊥AG，

（3）

如图a，

在△ABC中，P为其中任意一点．连接AP，BP，得到△ABP．
以点B为旋转中心，将△ABP逆时针旋转 60°，得到△EBD
∵旋转60°，且BD＝BP，
∴△DBP 为一个等边三角形
∴PB＝PD
∴PA+PB+PC＝DE+PD+PC
∴当E、D、P、C 四点共线时，为PA+PB+PC最小．


如图3，当B、P、G、D四点共线时，PA+PB+PC值最小，最小值为BD．
∵将△APC绕点C顺时针旋转60°，得到△DGC，
∴△APC≌△DGC，
∴CP＝CG，∠PCG＝60°，
∴△PCG是等边三角形，
∴PG＝CG＝CP，∠GPC＝∠CGP＝60°．
∵菱形ABCD中，∠ABP＝∠CBP＝∠ABC＝30°，
∴∠PCB＝∠GPC﹣∠CBP＝60°﹣∠30°＝30°，
∴∠PCB＝∠CBP＝30°，
∴BP＝CP，
同理，DG＝CG，
∴BP＝PG＝GD．
连接AC，交BD于点O，则AC⊥BD．
在Rt△BOC中，∵∠BOC＝90°，∠OBC＝30°，BC＝4，
∴BO＝BC•cos∠OBC＝4×＝2，
∴BD＝2BO＝4，
∴BP＝BD＝．
即当PA+PB+PC值最小时PB的长为．







1．（2020•重庆中考真题）如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D是BC边上一动点，连接AD，把AD绕点A逆时针旋转90°，得到AE，连接CE，DE．点F是DE的中点，连接CF．
（1）求证：CF＝AD；
（2）如图2所示，在点D运动的过程中，当BD＝2CD时，分别延长CF，BA，相交于点G，猜想AG与BC存在的数量关系，并证明你猜想的结论；
（3）在点D运动的过程中，在线段AD上存在一点P，使PA+PB+PC的值最小．当PA+PB+PC的值取得最小值时，AP的长为m，请直接用含m的式子表示CE的长．


【解答】证明：（1）∵AB＝AC，∠BAC＝90°，
∴∠ABC＝∠ACB＝45°，
∵把AD绕点A逆时针旋转90°，得到AE，
∴AD＝AE，∠DAE＝90°＝∠BAC，
∴∠BAD＝∠CAE，DE＝AD，
又∵AB＝AC，
∴△BAD≌△CAE（SAS），
∴∠ABD＝∠ACE＝45°，
∴∠BCE＝∠BCA+∠ACE＝90°，
∵点F是DE的中点，
∴CF＝DE＝AD；
（2）AG＝BC，
理由如下：如图2，过点G作GH⊥BC于H，

∵BD＝2CD，
∴设CD＝a，则BD＝2a，BC＝3a，
∵∠BAC＝90°，AB＝AC，
∴AB＝AC＝＝a，
由（1）可知：△BAD≌△CAE，
∴BD＝CE＝2a，
∵CF＝DF，
∴∠FDC＝∠FCD，
∴tan∠FDC＝tan∠FCD，
∴＝2，
∴GH＝2CH，
∵GH⊥BC，∠ABC＝45°，
∴∠ABC＝∠BGH＝45°，
∴BH＝GH，
∴BG＝BH
∵BH+CH＝BC＝3a，
∴CH＝a，BH＝GH＝2a，
∴BG＝2a，
∴AG＝BG﹣AB＝a＝CD＝BC；
（3）如图3﹣1，将△BPC绕点B顺时针旋转60°得到△BNM，连接PN，

∴BP＝BN，PC＝NM，∠PBN＝60°，
∴△BPN是等边三角形，
∴BP＝PN，
∴PA+PB+PC＝AP+PN+MN，
∴当点A，点P，点N，点M共线时，PA+PB+PC值最小，
此时，如图3﹣2，连接MC，

∵将△BPC绕点B顺时针旋转60°得到△BNM，
∴BP＝BN，BC＝BM，∠PBN＝60°＝∠CBM，
∴△BPN是等边三角形，△CBM是等边三角形，
∴∠BPN＝∠BNP＝60°，BM＝CM，
∵BM＝CM，AB＝AC，
∴AM垂直平分BC，
∵AD⊥BC，∠BPD＝60°，
∴BD＝PD，
∵AB＝AC，∠BAC＝90°，AD⊥BC，
∴AD＝BD，
∴PD＝PD+AP，
∴PD＝m，
∴BD＝PD＝m，
由（1）可知：CE＝BD＝m．