第19章 单元学考对接 同步典型例题精讲课件

这是一份第19章 单元学考对接 同步典型例题精讲课件，共56页。

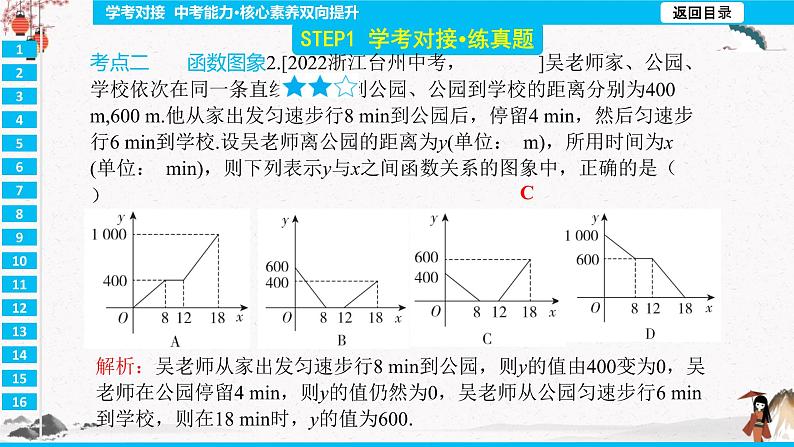
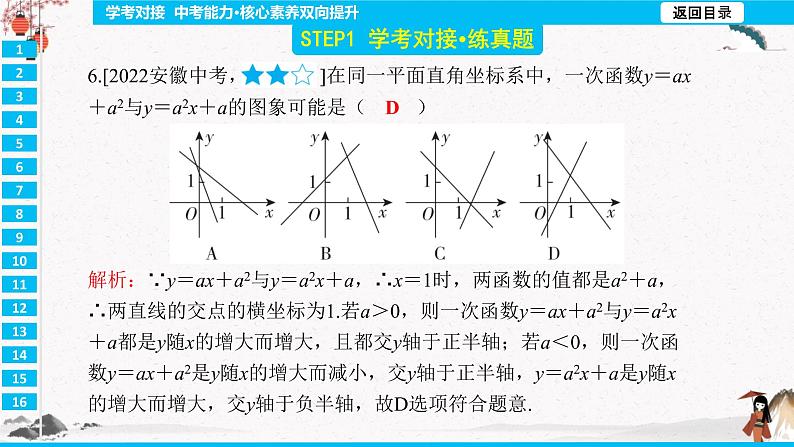
第十九章 一次函数 A 解析：由题意，得x－1≥0，∴x≥1. D 解析：∵当x＝0时，y＝1，∴一次函数y＝5x＋1的图象与y轴的交点的坐标为(0,1). D 解析：∵y＝ax＋a2与y＝a2x＋a，∴x＝1时，两函数的值都是a2＋a，∴两直线的交点的横坐标为1.若a＞0，则一次函数y＝ax＋a2与y＝a2x＋a都是y随x的增大而增大，且都交y轴于正半轴；若a＜0，则一次函数y＝ax＋a2是y随x的增大而减小，交y轴于正半轴，y＝a2x＋a是y随x的增大而增大，交y轴于负半轴，故D选项符合题意. B 解析：将直线y＝2x＋1向上平移2个单位后得到新直线的解析式为y＝2x＋1＋2，即y＝2x＋3.由于y＝2x＋3＝2(x＋1)＋1，所以将直线y＝2x＋1向左平移1个单位即可得到直线y＝2x＋3.y＝－x＋2(答案不唯一) x＜－1 解析：由图象可得，当x＝－1时，y＝3，该函数y随x的增大而减小，∴不等式kx＋b＞3的解集为x＜－1.D解析：由图象可得前10分钟，甲的速度为0.8÷10＝0.08(千米/分钟)，乙的速度是1.2÷10＝0.12(千米/分钟)，∴甲比乙的速度慢，故A正确，不符合题意；经过20分钟，甲、乙都走了1.6千米，故B正确，不符合题意；∵甲40分钟走了3.2千米，∴甲的平均速度为3.2÷40＝0.08(千米/分钟)，故C正确，不符合题意；∵经过30分钟，甲走过的路程是2.4千米，乙走过的路程是2.0千米，∴甲比乙走过的路程多，故D错误，符合题意.(2)该班准备采购A，B两种类型的羽毛球拍共30副，且A型羽毛球拍的数量不少于B型羽毛球拍数量的2倍，请给出最省钱的购买方案，求出最少费用，并说明理由.解：设购买B型羽毛球拍a副，总费用w元，则购买A型羽毛球拍(30－a)副.依题意，得30－a≥2a，解得a≤10.则w＝40(30－a)＋32a＝－8a＋1 200.∵－8＜0，∴w随a的增大而减小，∴当a＝10时，w取最小值，w最小＝－8×10＋1 200＝1 120.∴最省钱的购买方案是购买A型羽毛球拍20副，B型羽毛球拍10副，最少费用为1 120元. D 解析：根据函数定义，给出一个x值，y有唯一的值与它相对应，可知D选项中，y不是x的函数.B D 解析：由题意，得x＋2≥0且x2－9≠0，解得x≥－2且x≠3. B 解析：当k＞0时，函数图象经过第一、二、三象限；当k＜0时，函数图象经过第二、三、四象限，故B正确.5.一次函数y＝kx＋b(k≠0)的图象经过点A(－2，m)，B(－3，n)，不经过第一象限，则下列关系正确的是（ ）A.m＜n B.m＞n C.m＝n D.不能确定 A 解析：∵一次函数y＝kx＋b的图象不经过第一象限，∴k＜0，∴y随着x的增大而减小.∵－2＞－3，∴m＜n.A解析：根据题意，设小正方形运动的速度为v.分三个阶段：①小正方形向右未完全穿入大正方形，则S＝2×2－vt×1＝4－vt；②小正方形完全穿入大正方形，则S＝2×2－1×1＝3；③小正方形向右未完全穿出大正方形，则S＝2×2－[1－(vt－2)]×1＝1＋vt.分析选项可得，A符合，C中面积减少太多.8.把直线y＝－x－3向上平移m个单位长度后，与直线y＝2x＋4的交点在第二象限，则m的整数值有（ ）A.4个 B.5个 C.6个 D.7个 D 解析：由图可得，两人前行过程中的速度为3 600÷20＝180(米/分)，故选项A不符合题意；m的值是20－5＝15，n的值是180×15＝2 700，故选项B不符合题意；姐姐返回时的速度为2 700÷(45－15)＝90(米/分)，故选项C不符合题意；运动18分钟时两人相距180×(18－15)＋90×(18－15)＝810(米)，故选项D符合题意.二、填空题(每小题4分，共24分)11.已知点A(m，y1)，B(m＋1，y2)都在直线y＝2x－3上，则y2－y1＝　　　　. 2 解析：当x＝m时，y1＝2m－3，当x＝m＋1时，y2＝2(m＋1)－3＝2m－1，∴y2－y1＝2m－1－(2m－3)＝2.12.在正比例函数y＝kx中，y的值随着x值的增大而增大，则点P(3，k)在第　　　　　象限. 一　解析：∵在正比例函数y＝kx中，y的值随着x值的增大而增大，∴k＞0，∴点P(3，k)在第一象限.13.将函数y＝2x＋3的图象平移，使它经过点(2，－1)，则平移后的直线所对应的函数解析式为　　　　　　　. y＝2x－5 解析：设平移后的解析式为y＝2x＋b.将点(2，－1)代入，得－1＝4＋b，解得b＝－5.故平移后的直线所对应的函数解析式为y＝2x－5.14.定义[p，q]为一次函数y＝px＋q的特征数，若特征数为[t，t＋3]的一次函数为正比例函数，则这个正比例函数为　　　　　　. y＝－3x 解析：根据题意，特征数为[t，t＋3]的一次函数的解析式为y＝tx＋(t＋3).因为此一次函数为正比例函数，所以t＋3＝0，解得t＝－3.故正比例函数为y＝－3x.15.已知一次函数y＝2x＋4的图象与x轴、y轴分别相交于点A，B，在直线x＝4上有一点C，连接AC，BC，若△ABC是等腰三角形，则点C的坐标为　　　　　　　　　　　. (22 022－1,22 022) 解析：根据y＝x＋1可知，该直线与x轴的夹角是45°，且OA1＝1；再结合正方形条件，可以判定所有三角形都是等腰直角三角形.∴点A2的纵坐标是1＋1＝2；点A3的纵坐标是2＋2＝4.同理，点A4的纵坐标为8；…；点An的纵坐标是2n－1.∴当n＝2 023 时，点A2 023的纵坐标为22 022，将y＝22 022代入y＝x＋1，得x＝22 022－1.∴点A2 023的坐标为(22 022－1,22 022).三、解答题(共66分)17.(8分)已知y＋1与x－2成正比例，且当x＝1时，y＝－3.(1)求y与x之间的函数解析式；(2)判断点(－1，－5)是否在该函数的图象上.解：(1)设y＋1＝k(x－2)(k≠0).把x＝1，y＝－3代入，得－3＋1＝k(1－2)，解得k＝2，∴y＝2(x－2)－1＝2x－5，即y与x之间的函数解析式为y＝2x－5.(2)当x＝－1时，y＝2×(－1)－5＝－7≠－5，∴点(－1，－5)不在该函数的图象上.(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论：①　　　　　　；②　　　　　　；③　　　　　　；④　　　　　　；(2)如果点C的坐标为(1,3)，那么不等式kx＋b≤k1x＋b1的解集为　　　.19.(10分)在平面直角坐标系中，已知点A(1,1)，B(2,2)，C(0,3).(1)求直线BC的解析式；(2)求直线BC与坐标轴所围成的三角形的面积；(3)若直线y＝kx＋3与线段AB有公共点，直接写出k的取值范围.(2)求y与x之间的函数解析式(不要求写出x的取值范围)；(3)王叔叔根据经验判断，该种经济作物平均高度在1.5 m左右时产量最高，此时每公顷应喷施约多少药物？(3)由于开通新的线路，使乙基地运往B城的运费每吨减少a(a＞0)元，其余路线运费不变.若总运费的最小值不少于10 020元，求a的最大整数解.(2)求△ADE的面积；(3)现把线段AB沿y轴平移a个单位长度，平移后的线段AB与(1)问中得到的线段CD组成新图象G，琪琪认为当平移的单位长度1≤a≤3时，图象G的最高点、最低点的纵坐标之差是一个不大于5的固定数值，大家经反复演算，发现琪琪的说法不正确，请通过计算解释琪琪的说法为什么不正确.解：线段AB沿y轴向上平移a个单位长度时，①当点B平移后不超过点C时，即1≤a≤2时，点B(0,2＋a)，A(－4，a)，此时图象G的最高点为点C，最低点为点D.∵C(0,4)，D(2,0)，∴纵坐标之差总为4，故纵坐标之差为一个不大于5的固定数值；②当点B平移后超过点C时，即2