








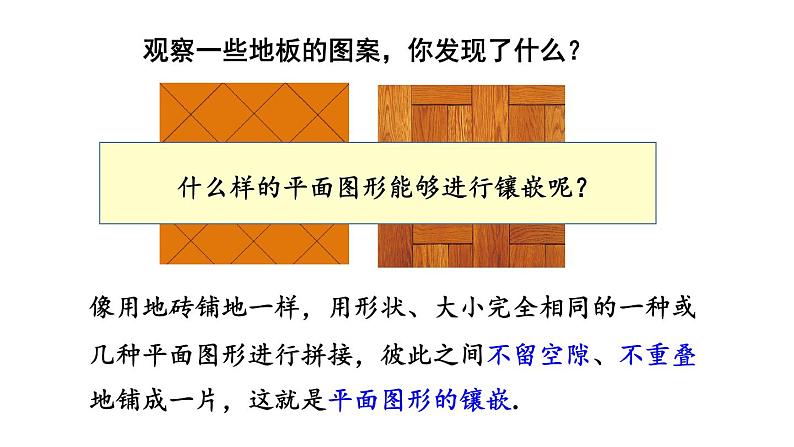


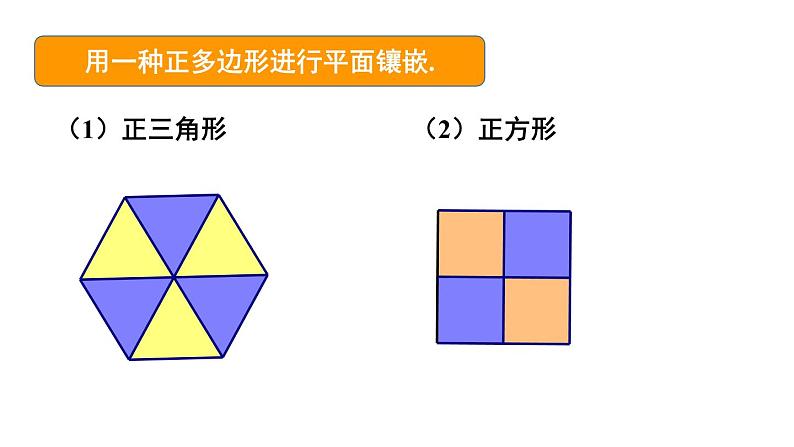
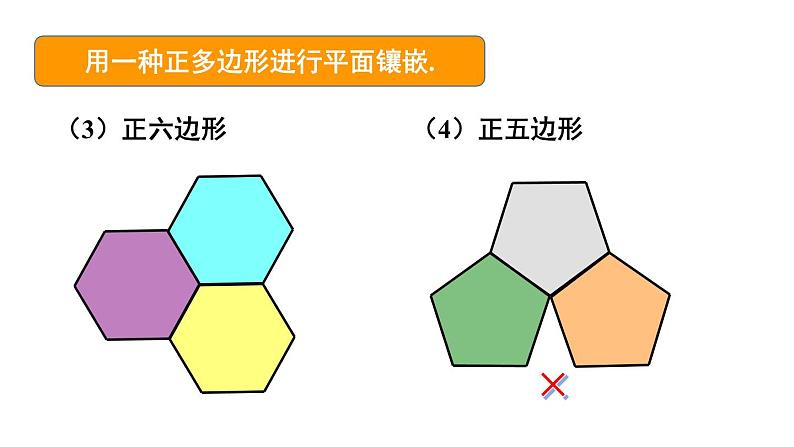
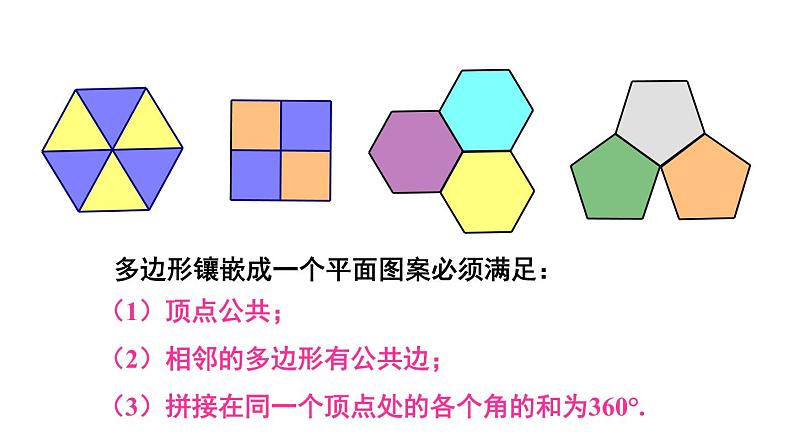



2 章末复习(3课时)课件+教案
展开章末复习
【知识与技能】
1.理解四边形、平行四边形、矩形、菱形、正方形的有关概念;掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法.
2.能灵活运用特殊四边形的知识解决一些实际问题.
【过程与方法】
经历探究四边形、平行四边形、矩形、菱形、正方形之间的联系与区别的过程,类比掌握平行四边形、矩形、菱形、正方形的性质与常用的判别方法.
【情感态度】
在回顾与思考的过程中,让学生进一步领会特殊与一般的关系,逐渐理解类比、转化等一些重要的数学思想.
【教学重点】
建立知识结构,掌握特殊四边形之间的联系与区别.
【教学难点】
灵活运用所学知识解决有关问题.
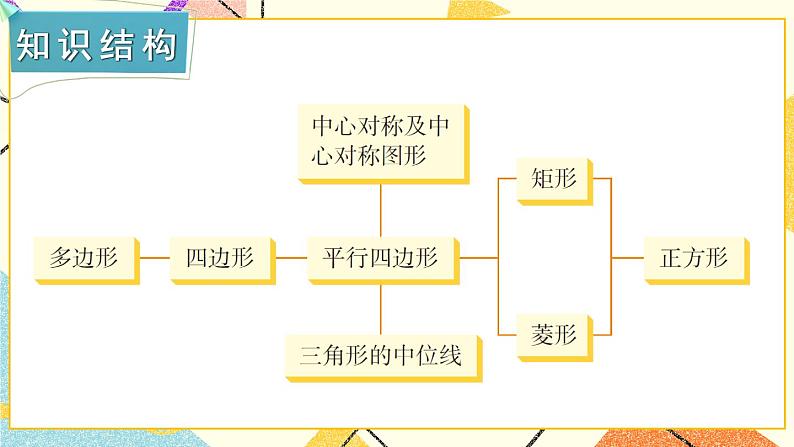
一、知识框图,整体把握
二、释疑解惑,加深理解
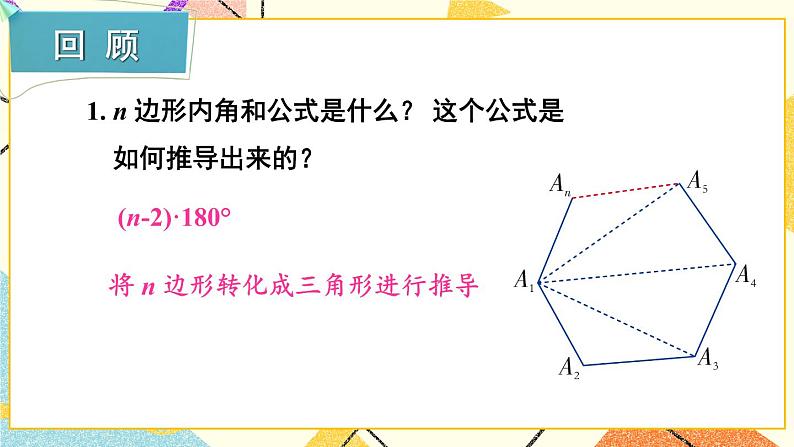
1.多边形的边数与内角和、外角和
由于多边形的外角和等于360°是一个固定的值,求多边形的边数和内角和往往可以从外角和入手,使计算更简便.
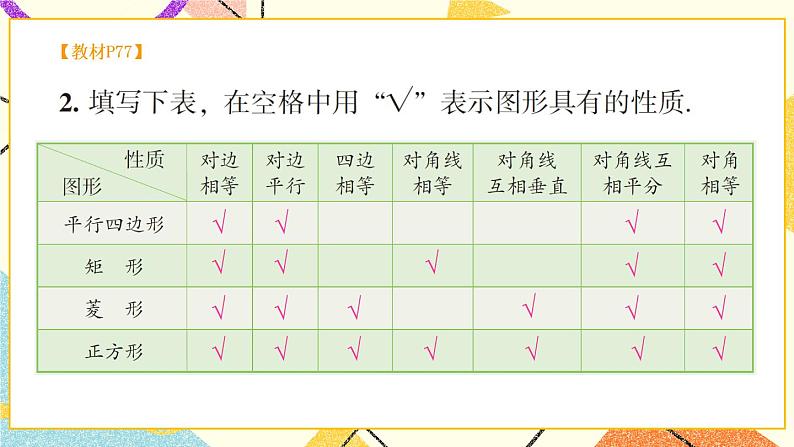
2.平行四边形和特殊平行四边形的性质与判定
特殊平行四边形都具有平行四边形的性质,并且有它本身独有的性质与判定,学习过程中注意不能相互混淆.
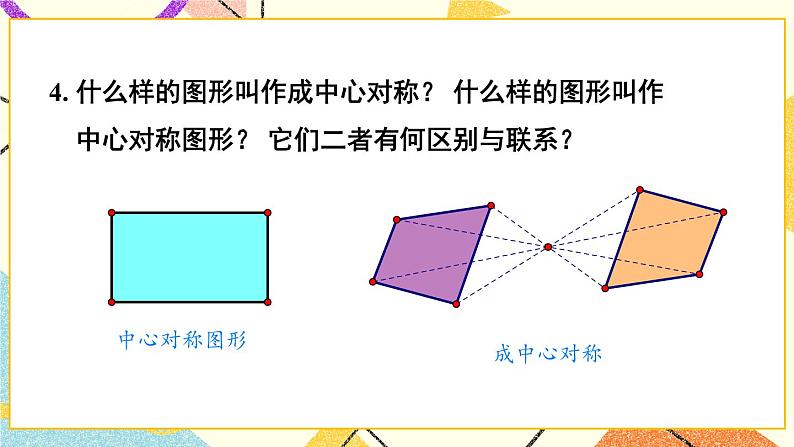
3.中心对称与中心对称图形
成中心对称是对两个图形来说的,它表示两个图形之间的对称关系,中心对称图形是对一个图形说的,它表示某个图形的特征.
三、典例精析,复习新知
例1 一个多边形的某一个外角与所有内角的总和为1350°,求边数n和这个外角的度数.
【分析】本题重点检验多边形的内角和是180°的整数倍的理解应用能力,注意到每一个外角都大于0°小于180°,可得不等式求解.
【解答】由多边形的任一个外角都大于0°小于180°,则有1350°-180°<(n-2)·180°<1350°,解得812<n<912.因为n为整数,所以n=9,这个外角的度数为1350°-(9-2)·18°=90°.
例2 如图,△ABC中,D在AB上,E在AC的延长线上,BD=CE,连结DE,交BC于F,∠BAC外角的平分线交BC的延长线于G,且AG∥DE,求证:BF=CF.
【分析】过点C作CM∥AB交DE于点M,可以证明BD=CM,然后再利用平行四边形的性质得到BF=CF.
证明:过点C作CM∥AB交DE于点M,连结BM、CD,则∠CME=∠ADE,∵AG∥DE,∴∠EAG=∠E=∠ADM.又∵AB∥CM,∴∠ADM=∠CME,∴∠CME=∠CEM,∴CM=CE=BD.∵BDCM,∴四边形BMCD为平行四边形,∴BF=CF.
例3 在矩形ABCD中,AB=2AD,E是CD上一点,且AE=AB,则∠CBE的度数是( )
A.30° B.22.5° C.15° D.以上答案都不对
【分析】因为AE=AB=2AD,所以∠AED=30°,可求出∠EAB=30°,△AEB为等腰三角形,∠CBE=90°-∠EBA.
解:∵四边形ABCD为矩形,∴AB∥CD,∠D=∠CBA=90°,∴∠AED=∠BAE,∵AB=2AD,AE=AB,∴AE=2AD,∠AED=30°,∴∠BAE=30°,∴∠ABE==75°,∴∠CBE=90°-∠ABE=90°-75°=15°.
例4 如图,有一矩形纸片ABCD,AB=6cm,BC=8cm,将纸片沿EF折叠,使点B与D重合,求折痕EF的长.
【分析】本题利用矩形性质,勾股定理及面积公式,显然折痕在BD的垂直平分线上,不难证得四边形BFDE为菱形,只要求ED的长问题就容易解决.
解:连BD,BE,DF,由折叠的实际意义可知EF⊥BD,且EF平分BD,∴BE=ED,BF=FD,∵矩形ABCD,∴AB=CD,AD=BC,∠C=90°,AD∥BC,∴∠EDO=∠FBO,又∵BO=DO,∠BOF=∠DOF,∴△BOF≌△DOE,∴ED=BF,∴ED=BF=FD=BE,∴四边形BFDE为菱形,∴菱形BFDE的面积=×BD×EF=BF×CD,设BF=x=DF则FC=8-x,依题意有:x2=(8-x)2+62,解得x=,又BD2=BC2+CD2=82+62,BD=10,∴×10×EF=×6,∴EF=.
例5 如图(1)在正方形ABCD的BC、CD边上取E、F两点,使∠EAF=45°,AG⊥EF于G,求证:AG=AB.
【分析】欲证AG=AB,就图形直观来看,应证Rt△ABE与Rt△AGE全等,但条件不够,∠EAF=45°怎么用呢?显然∠1+∠2=45°,若把它们拼在一起,问题就解决了.
证明:把△AFD绕点A旋转90°至△AHB(或延长EB至H使BH=DF),如图(2).∵∠EAF=45°,∴∠1+∠2=45°,∵∠2=∠3,∴∠1+∠3=45°,又由旋转所得AH=AF,AE=AE,∴△AEF≌△AEH(SAS),∴AG=AB.
【教学说明】典型例题的分析,对于学生解题有着重要的指导作用,特别是开阔了学生的眼界,拓展了学生的解题思路和方法.教师在讲评的过程中,要让学生明确本章的重点和难点,容易出错或忽略的地方重点强调,逐步提高.
四、复习训练,巩固提高
1.一个正多边形的每个外角都等于36°,那么它是 边形.
2.在□ABCD中,对角线AC=12cm,BD=8cm,交点为O,若△AOB与△BOC的周长和为37cm,则□ABCD的周长为 cm.
3.下列图形是中心对称图形而不是轴对称图形的是( )
4.如果三角形的两边分别为3和5,那么连接这个三角形三边中点所得的三角形的周长可能是( )
A.5.5 B.5 C.4.5 D.4
5.如图所示,在ABCD中,已知AD=10cm,AB=4cm,AE平分∠BAD交BC于点E,则EC等于( )
A.7cm B.6cm
C.5cm D.4cm
6.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:BE=DF;
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM,判断四边形AEMF是什么特殊四边形?并证明你的结论.
【教学说明】这部分安排了本章几个重点知识的运用,目的是为了检测学生的掌握情况,有利于及时发现错误,并有针对性查漏补缺.
【答案】1.十 2.34 3.A 4.A 5.B
6.(1)证Rt△ABE≌Rt△ADF,得BE=DF.(2)四边形AEMF是菱形,证明:∵四这形ABCD是正方形,∴∠BCA=∠DCA=45°,BC=DC,∵BE=DF,∴BC-BE=DC-DF,即CE=CF,∴△EOC≌△FOC,∴OE=OF,∵OM=OA,∴四边形AEMF是平行四边形,∵AE=AF,∴平行四边形AEMF是菱形.
五、师生互动,课堂小结
你能完整地回顾本章所学的四边形、平行四边形、特殊的平行四边形的有关知识吗?你认为哪些内容是大家需要掌握的?学习过程中还有哪些困惑?请与同学们共同交流探讨.
【教学说明】通过师生共同回顾本章所学知识,让学生自主讨论、交流形成共识,易错的地方作必要的强调补充.
1.布置作业:从复习题中选取.
2.完成练习册.
本节课从整理本章主要内容入手,用精选的例题为范本,让学生运用所学知识解决问题,并且通过训练使所学内容全面得到强化,能力逐步提高.第3章图形与坐标









