

广东省广州市番禺区2022-2023学年七年级上学期期末数学试卷
展开
这是一份广东省广州市番禺区2022-2023学年七年级上学期期末数学试卷,共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省广州市番禺区七年级(上)期末数学试卷 一、选择题(本题共10小题,共30分)1. 如果气温升高时气温变化记作,那么气温下降时气温变化记作( )A. B. C. D. 2. 的绝对值等于( )A. B. C. D. 3. 关于单项式,下列说法中正确的是( )A. 它的次数是 B. 它系数是 C. 它系数是 D. 它的次数是4. 庆祝新中国成立周年,国庆假期期间,各旅游景区节庆氛围浓厚,某景区同步设置的“我为祖国点赞”装置共收集约个“赞”,这个数字用科学记数法可表示为( )A. B. C. D. 5. 一个正方体的表面展开图如图所示,则原正方体的“我”字所在面的对面所标的字是( )A. 美
B. 丽
C. 番
D. 附6. 下列计算正确的是( )A.
B.
C.
D.
7. 已知是方程的解,则的值是( )A.
B.
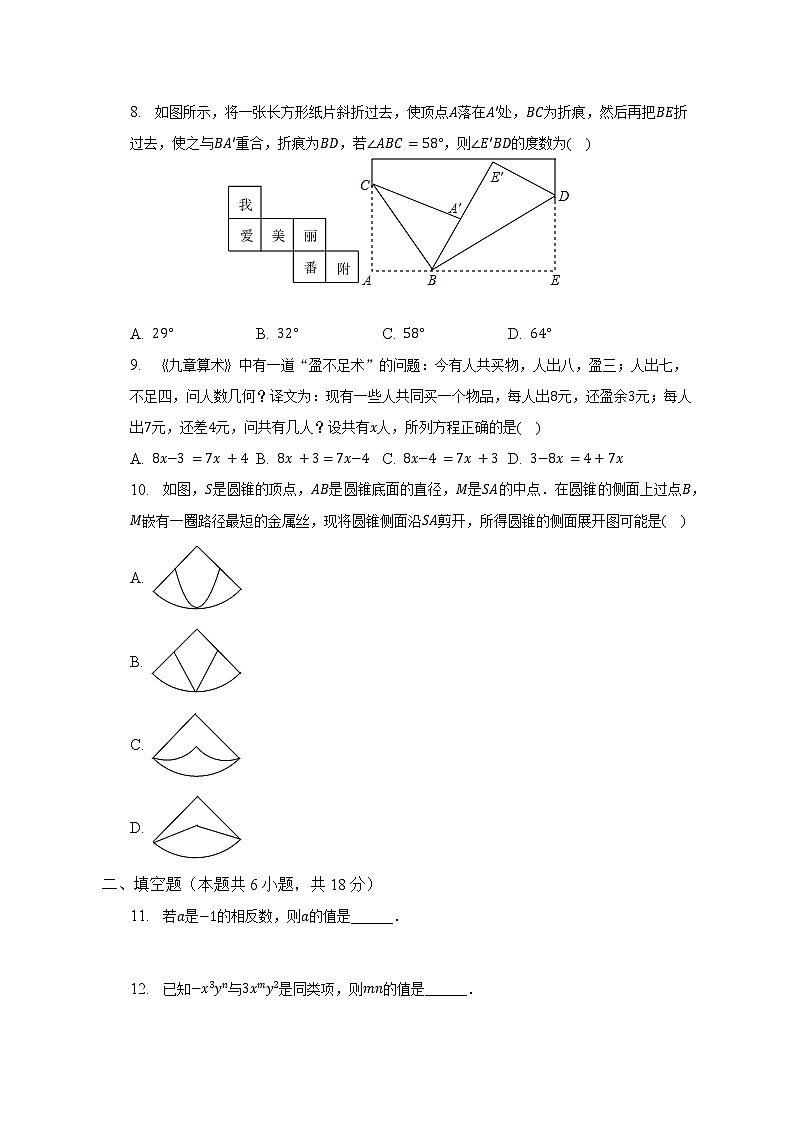
C.
D. 8. 如图所示,将一张长方形纸片斜折过去,使顶点落在处,为折痕,然后再把折过去,使之与重合,折痕为,若,则的度数为( )A. B. C. D. 9. 九章算术中有一道“盈不足术”的问题:今有人共买物,人出八,盈三;人出七,不足四,问人数几何?译文为:现有一些人共同买一个物品,每人出元,还盈余元;每人出元,还差元,问共有几人?设共有人,所列方程正确的是( )A. B. C. D. 10. 如图,是圆锥的顶点,是圆锥底面的直径,是的中点.在圆锥的侧面上过点,嵌有一圈路径最短的金属丝,现将圆锥侧面沿剪开,所得圆锥的侧面展开图可能是( )A.
B.
C.
D. 二、填空题(本题共6小题,共18分)11. 若是的相反数,则的值是______.
12. 已知与是同类项,则的值是______.
13. 计算的结果为______.
14. 如图,某海域有三个小岛,,,在小岛处观测到小岛在它北偏东的方向上,观测到小岛在它南偏东的方向上,则的度数是 .15. 已知、、三点在同一条直线上,且,,则______.16. 如图所示,用火柴拼成一排由个三角形组成的图形,需要______根火柴棒,小亮用根火柴棒,可以拼出______个三角形.
三、解答题(本题共9小题,共72分)17. 计算:
;
.18. 解方程:
;
.19. 如图,已知平面上三点,,,请按要求完成下列问题:
尺规作图:画射线,线段;
连接,延长线段至点,使得,连接;
用量角器度量得______精确到度.
20. 已知,.
求;
当,,求代数式的值.21. 羽毛球的标准重量为,在检测其重量是否标准时,把超过标准重量的部分用正数,低于标准重量的部分用负数表示.下面是五个羽毛球的重量检测记录单位::,,,,.
其中最标准和最不标准的羽毛球各重多少?
这个羽毛球共重多少?平均每个羽毛球重多少?22. 如图,点在线段上,,,点、分别是、的中点.
求线段的长;
若点在线段的延长线上,且满足,其它条件不变,你能猜想的长度吗?请画出图形,写出你的结论,并说明理由.
23. 我校在科技节的系列活动中举行了“王中王”知识竞赛,共设道选择题,各题分值及得分标准相同,每题必答,未作答视为答错.下表记录了其中个参赛者的得分情况.参赛者答对题数答错题数得分参赛者答对一题得______分,答错一题得______分;
参赛者小红得了分,她答对了几道题?
参赛者小明说他得了分,你认为可能吗?为什么?24. 如图,是一个计算装置示意图,、是数据输入口,是计算输出口,计算过程是由、分别输入自然数和,经计算后得自然数由输出,此种计算装置完成的计算满足以下三个性质:
若,时,:
若输入任何固定的自然数不变,输入自然数增大,则比原来增大;
若输入任何固定的自然数不变,输入自然数增大,则为原来的倍.
试解答以下问题:
当,时,求的值;
当,时,求的值;
当,时,求的值.
25. 如图,为直线上一点,将两个直角三角板的顶点叠合在处,其中一个直角三角板的另一顶点也叠合在直线上的点处.
在如图的位置,若射线是的平分线,试判断射线是否为的平分线?并说明理由;
在如图的位置,若,求的大小;
将直角三角板绕点逆时针方向旋转,旋转角度不超过度,在旋转过程中,试探究与之间满足什么等量关系,并说明理由.
答案和解析 1.【答案】 【解析】【分析】
本题主要考查了正负数的意义及其应用,要熟练掌握,解答此题的关键是要明确:气温上升记为“”,则气温下降记为“”.
根据正负数的意义,可得气温上升记为“”,则气温下降记为“”,据此解答即可.
【解答】
解:如果气温升高时气温变化记作,那么气温下降时气温变化记作.
故选B. 2.【答案】 【解析】解:根据绝对值的性质,
.
故选:.
根据绝对值的性质:一个负数的绝对值是它的相反数解答即可.
本题考查了绝对值的性质:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,的绝对值是,难度适中.
3.【答案】 【解析】解:根据单项式系数、次数的定义可知:
单项式的系数是;次数是.
故选:.
根据单项式系数、次数的定义来求解.单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
确定单项式的系数和次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式的系数和次数的关键.
4.【答案】 【解析】【分析】
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
根据科学记数法的表示方法解答即可.
【解答】
解:,
故选:. 5.【答案】 【解析】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
原正方体的“我”字所在面的对面所标的字是“番”.
故选:.
正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
6.【答案】 【解析】【分析】
此题考查了合并同类项以及去括号,熟练掌握运算法则是解本题的关键.计算各式得到结果,即可作出判断.
【解答】
解:、原式,不符合题意;
B、原式,符合题意;
C、原式,不符合题意;
D、原式不能合并,不符合题意.
故选:. 7.【答案】 【解析】【分析】
本题主要考查一元一次方程的解的定义,掌握方程的解满足方程是解题的关键.把代入方程可得到关于的方程,解方程可求得的值.
【解答】
解:因为是方程的解,
所以把代入方程可得,
解得,
故选:. 8.【答案】 【解析】【分析】
本题考查了角的有关计算和折叠的性质,能根据折叠的性质得出和是解此题的关键.根据折叠得出,,根据,求出,代入求出即可.
【解答】
解:根据折叠得出,,
又,
,
,
.
故选:. 9.【答案】 【解析】解:设共有人,
根据题意得:,
故选:.
根据该物品的价格不变即可得出关于的一元一次方程.
本题主要考查由实际问题抽象出一元一次方程,解题的关键是理解题意,确定相等关系.
10.【答案】 【解析】解:利用圆锥侧面展开图是扇形,再利用是的中点,在圆锥的侧面上过点,嵌有一圈路径最短的金属丝,
现将圆锥侧面沿剪开,所得圆锥的侧面展开图可能是选项B.
故选:.
利用圆锥侧面展开图的性质结合为中点,并且将圆锥侧面沿剪开,进而得出符合题意的图形.
此题主要考查了几何体的展开图,正确把握圆锥侧面展开图的性质是解题关键.
11.【答案】 【解析】解:的相反数是,即,
故答案为:.
求出的相反数即可.
本题考查相反数,理解相反数的定义是正确解答的前提.
12.【答案】 【解析】解:与是同类项,
,,
则.
故答案为:.
直接利用所含字母相同,并且相同字母的指数也相同,这样的项叫做同类项,进而得出,的值,即可分析得出答案.
此题主要考查了同类项,正确把握同类项的定义是解题关键.
13.【答案】 【解析】解:
,
故答案为:.
根据度、分、秒的换算方法进行计算即可.
本题考查度、分、秒的换算,掌握度、分、秒的换算方法以及单位之间的进率是正确解答的前提.
14.【答案】 【解析】【分析】
本题考查了方向角及角的计算.解题的关键是明确方向角中角之间的关系,以及角的和差计算.
根据已知条件可直接确定的度数.
【解答】
解:因为在小岛北偏东的方向上,在小岛南偏东的方向上,
所以,
故答案为:. 15.【答案】或 【解析】解:当在线段上时:;
当在的延长线上时,.
故答案是:或.
A、、在同一条直线上,则可能在线段上,也可能在的延长线上,应分两种情况进行讨论.
此题主要考查了两点之间的距离求法,求线段的长度,能分两种情况进行讨论是解决本题的关键.
16.【答案】 【解析】解:观察图形的变化可知:
由个三角形组成的图形,需要根火柴棒;
由个三角形组成的图形,需要根火柴棒;
由个三角形组成的图形,需要根火柴棒;
,
发现规律:
由个三角形组成的图形,需要根火柴棒;
由个三角形组成的图形,需要根火柴棒;
因为,
所以,
所以用根火柴棒,可以拼出个三角形.
故答案为:;.
观察图形的变化先求出前几个图形需要的火柴棒根数,即可发现规律:由个三角形组成的图形,需要根火柴棒,进而可求几个.
本题考查了规律型:图形的变化类,解决本题的关键是根据图形的变化寻找规律.
17.【答案】解:原式
;
原式
. 【解析】减法转化为加法、计算绝对值,再计算加减即可;
先计算乘方和括号内的运算,再计算乘除,最后计算加法即可.
本题主要考查有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和运算法则.
18.【答案】解:,
移项,得,
合并同类项,得,
系数化成,得;
,
去分母,得,
去括号,得,
移项,得,
合并同类项,,得,
系数化成,得. 【解析】移项,合并同类项,系数化成即可;
去分母,去括号,移项,合并同类项,系数化成即可.
本题考查了解一元一次方程,能正确根据等式的性质进行变形是解此题的关键.
19.【答案】 【解析】解:如图:
用量角器度量得.
故答案为:.
根据要求画出图形即可;
根据要求画出图形即可;
用量角器度量的度数即可.
本题考查了作图基本作图,射线、线段的定义,正确画出图形是解题的关键.
20.【答案】解:
;
当,时,
得:,
则. 【解析】把相应的式子代入,利用合并同类项的法则进行运算即可;
把的值代入,再利用,从而可求解.
本题主要考查整式的加减,解答的关键是对相应的运算法则的掌握.
21.【答案】解:,,;,,
,
最标准的球重:,
最不标准的求重:.
答:其中最标准的羽毛球重,最不标准的羽毛球重;
这个羽毛球共重:,
平均每个羽毛球重:.
答:这个羽毛球共重,平均每个羽毛球重. 【解析】根据绝对值最小的是最标准的,绝对值最大的是最不标准的,可得最标准和最不标准的球重;
根据有理数的加法运算,可得球的总重量,根据球的总重量除以球的个数,可得平均重量.
本题考查了正数和负数的知识,掌握正数和负数的含义是关键.
22.【答案】解:点在线段上,,,点、分别是、的中点,
,,
;
如图所示,
点在线段的延长线上,且满足,
又点、分别是、的中点,
,,
,
的长度. 【解析】利用线段的和差,线段的中点的性质计算;
先画出图形,再利用线段的和差,线段的中点的性质计算.
本题考查了两点间的距离,解题的关键是掌握线段的和差,线段中点的性质.
23.【答案】 【解析】解:设答对一道得分,
根据的得分情况可得:,
解得,
根据的得分情况可得答错一道得:分,
故答案为:,;
设参赛者小红答对了道题,
根据题意得:,
解得,
参赛者小红答对了道题;
参赛者小明不可能得分,理由如下:
设参赛者小明答对了道题,
根据题意得:,
解得,
为整数,
参赛者小明不可能得分.
设答对一道得分,根据的得分情况得,解得,根据的得分情况可得答错一道得分;
设参赛者小红答对了道题,得:,可解得答案;
设参赛者小明答对了道题,得:,解得,故参赛者小明不可能得分.
本题考查一元一次方程的应用,解题的关键是读懂题意,列出一元一次方程.
24.【答案】解:因为当,时,.
若输入任何固定的自然数不变,输入自然数增大,则比原来增大,
所以当,时,.
当,时,.
当,时,.
因为若,时,.
若输入任何固定的自然数不变,输入自然数增大,则为原来的倍.
所以当,时,.
当,时,.
当,时,.
当,时,.
当,时,.
当,时,.
当,时,.
当,时,.
当,时,.
当,时,,
故或. 【解析】此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.
根据若输入任何固定的自然数不变,输入自然数增大,则比原来增大,即可求得当,时,的值;
根据若输入任何固定的自然数不变,输入自然数增大,则为原来的倍.即可求得当,时,的值;
由得出,,根据若输入任何固定的自然数不变,输入自然数增大,则比原来增大,即可求出当,时,的值;由得,当,时,,再由若输入任何固定的自然数不变,输入自然数增大,则比原来增大,即可求得当,时,的值.
25.【答案】解:射线是的平分线,
,
,
,
射线是的平分线;
,
,
;
的大小为;
当在的右侧时,
由图可知,,,
;
当在的左侧时,
由图可知,,
,
,
当在上方时,如图,
由图可知,,,
;
综上可知,和互补. 【解析】利用角的和差计算并判断;
利用角的和差计算;
读懂题意,掌握旋转的过程,发现与之间存在互补的关系.
本题主要考查角度的和差计算,涉及补角的定义,余角的定义,角平分线的定义等相关知识,由图形得到角度之间的和差关系是解题关键.
相关试卷
这是一份广东省广州市番禺区星海中学2022-2023学年八年级上学期期末检测+数学试卷(问卷),共3页。试卷主要包含了选择题,填空题,计算题,作图题等内容,欢迎下载使用。
这是一份广东省广州市番禺区桥城中学2022-2023学年九年级上学期期末数学试卷,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份广东省广州市番禺区钟村中学2022-2023学年九年级上学期期末数学试卷,共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。










