沪科版七年级下册6.1 平方根 、立方根优秀课件ppt

这是一份沪科版七年级下册6.1 平方根 、立方根优秀课件ppt，文件包含第2课时算数平方根ppt、第1课时平方根课件ppt、1平方根教案doc等3份课件配套教学资源，其中PPT共39页， 欢迎下载使用。
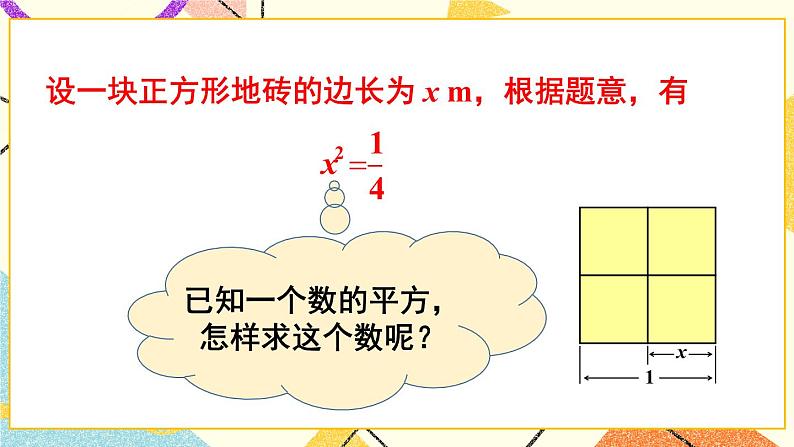
第6章 实数6.1平方根、立方根1.平方根【知识与技能】1.掌握平方根、算术平方根的概念，明确平方根和算术平方根之间的联系和区别；2.能用符号表示一个数的平方根和算术平方根，理解开平方运算和平方运算之间的互逆关系.会求一个非负数的平方根和算术平方根.3.理解并运用a的双重非负性.【过程与方法】通过观察、理解开平方运算和平方运算之间的互逆关系，掌握求一个非负数的平方根和算术平方根的方法，培养学生的观察、演绎能力.【情感态度】有意识地引导学生积极参与到数学活动过程中，培养学生的观察、归纳能力，通过合作学习体验成功的喜悦，激发学生学习数学的兴趣.【教学重点】能用符号正确表示一个数的平方根和算术平方根，理解开平方运算和平方运算之间的互逆关系，会求一个非负数的平方根和算术平方根.【教学难点】理解并运用a的双重非负数.一、情境导入,初步认识问题  装修房屋，选用了某种型号的正方形地砖，这种地砖4块正好铺1m2，如图（单位：m)，问这种地砖的一块的边长是多少？【教学说明】教师提出问题后，让学生独立思考，然后让学生相互交流.学生很容易设出未知数，列出方程，感受平方根，算术平方根是实际的需要，激发学生探求新知识的欲望.二、思考探究，获取新知1.平方根的定义.问：已知一个数的平方，怎样求这个数呢？【教学说明】教师提出问题，同学生一起分析，引出平方根的定义.【归纳结论】一般地，如果一个数的平方等于a,那么这个数叫做a的平方根，也叫做二次方根.2.平方根的性质.问：（1）16的平方根是什么？（2）0的平方根是什么？(3)-9有没有平方根？【教学说明】教师提出问题，学生独立完成再和同伴进行交流，归纳平方根的性质.【归纳结论】一个正数a的平方根有两个，它们互为相反数,0的平方根是0，负数没有平方根.正数a的正的平方根，叫做a的算术平方根，记为 ，其中a叫做被开方数，另一个负的平方根记为-，0的算术平方根是0.求一个数的平方根的运算叫做开平方.开方是平方的逆运算.根据这种关系，可以求出一些数的平方根.三、典例精析，掌握新知例1 判断下列各数是否有平方根，为什么？25;     ;    0.0169;     -64.【解】∵正数和零有平方根，负数没有平方根.∴25, ,0.0169有平方根；-64没有平方根.例2求下列各数的平方根和算术平方根.（1）1;(2)81;(3)64;(4)(-3)2.【解】（1）∵(±1)2=1,∴1的平方根是±1，即±=±1;1的算术平方根是1.(2)∵(±9)2=81.∴81的平方根是±9，即±=±9;81的算术平方根是9.（3）∵(±8)2=64,∴64的平方根是±8，即±=±8;64的算术平方根是8.（4）∵(-3)2=9,9的平方根是±3,∴(-3)2的平方根是±3，即±=±3;（-3）2的算术平方根是3.【教学说明】让学生自主完成，掌握求一个数的平方根和算术平方根的方法.【归纳结论】对于一些平方数，我们可以根据开平方与平方的互逆关系，求出这些数的平方根和算术平方根.例3 利用计算器求下列各式的值（精确到0.01）:(1) ;    (2) ;    (3) -;   (4) .【解】(1) ≈1.41(2) ≈42.78(3) -≈-0.94(4) ≈0.85例4 跳水运动员要在空中下落的短暂过程中完成一系列高难度的动作，如果不考虑空气阻力等其他因素影响，弹跳到最高点后，人体下落到水面所需要的时间t与下落的高度h之间应遵循下面的公式：h=gt2.其中h的单位是m，t的单位是s，g=9.8m/s2.假设跳板的高度是3m，运动员在跳板上起跳至高出跳板1.2m处开始下落，那么运动员下落到水面约需多长时间？【解】设运动员下落到水面约需ts，根据题意，得3+1.2=×9.8t2∴运动员下落到水面约需0.93s.【教学说明】让学生自主探究、相互交流，掌握计算器的使用方法，并能借助计算器求一些数的平方根，对于例4这样的实际问题，可设未知数列出方程，而解x2=a这样的方程，可看作是求a的平方根.【归纳结论】对于一些非平方数，可以利用计算器求出它们的平方根.四、运用新知，深化理解1.填空：(1)一个正数有两个平方根，而且这两个平方根           ;(2)           有且只有一个平方根，它的平方根就是           ;(3)           数没有平方根.2.判断是非.(1)4是16的算术平方根.(        )(2) 是的一个平方根.(        )(3)(-5)2的平方根是-5.(        )(4)0的算术平方根是0.(        )3.下列的各式是否有意义，说明理由:4.求下列各数的平方根，算术平方根，并用式子表示.(1)49；(2)25.5.用计算器求下列各式的值（精确到0.01)：6.一个正数x的两个平方根分别是2a-1与-a+2,求a和x.7.若|2014-a|+=0.求a-b的值.【教学说明】学生自主探究，教师巡视，及时给予指导.【答案】1.（1）互为相反数   （2）0   0     （3）负2.（1）√(2)√(3)×(4)√3.（1）（3）（4）有意义（2）无意义，理由略4. 6.由2a-1-a+2=0得a=-1,当a=-1时，x=(2a-1)2=(-3)2=9.7.由2014-a=0,b-2015=0得a=2014,b=2015,∴a-b=2014-2015=-1.五、师生互动，课堂小结通过这节课的学习，你掌握了哪些新知识？还有哪些疑问？请与同伴交流.【教学说明】学生相互交流，回顾知识点，反思问题，共同提高.完成练习册中本课时练习.从实际问题引出平方根和算术平方根，学生积极主动探索，教师引导与启发，激发学生学习兴趣.