【新高考】2023年高考数学二轮复习精讲精练学案——第01讲 集合（原卷版+解析版）

这是一份【新高考】2023年高考数学二轮复习精讲精练学案——第01讲 集合（原卷版+解析版），文件包含第一讲集合讲义解析版docx、第一讲集合讲义原卷版docx等2份学案配套教学资源，其中学案共19页， 欢迎下载使用。

集合及其关系
集合中元素的特性：确定性、互异性、无序性.
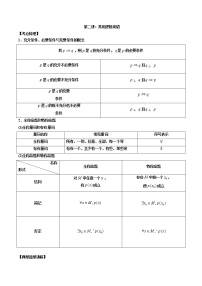
集合间的基本关系
注意：（1）空集是任何集合的子集；（2）空集是任何非空集合的真子集；（3）若有限集中有个元素，则集合的子集个数为，真子集的个数为.
集合的基本运算
【典型题型讲解】
考点一：集合的概念：集合表示，元素的性质
【典例例题】
例1．集合，用列举法可以表示为_________．
【答案】##
【详解】
因为，所以，可得，因为，所以，集合．
故答案为：
例2、已知集合，集合，则（ ）
A．B．C．D．
【答案】C
【详解】
，，
,
故选：C
例3、设集合，若且，则实数的取值范围是（ ）
A．B．C．D．
【答案】C
【详解】
因为集合，而且，
且，解得．
故选：C．
【方法技巧与总结】
1.列举法，注意元素互异性和无序性，列举法的特点是直观、一目了然.
2.描述法，注意代表元素.
3.研究集合问题，看元素是否满足集合的特征：确定性、互异性、无序性。
【变式训练】
1、已知集合，，则集合中元素个数为（ ）
A．2B．3C．4D．5
【答案】C
【详解】
解：因为，，所以或或或，
故，即集合中含有个元素；
故选：C
2、设集合，，则集合中元素个数为（ ）
A．B．C．D．无数个
【答案】B
【详解】
由，解得，故，，
故，集合中元素个数为3.
故选：B.
3、定义集合的一种运算：，若，，则中的元素个数为（ ）
A．B．C．D．
【答案】C
【详解】
因为，，，
所以，
故集合中的元素个数为3，
故选：C.
4、已知集合，， ，则C中元素的个数为（ ）
A．1B．2C．3D．4
【详解】
由题意，当时， ，当，时， ，
当，时， ，
即C中有三个元素，
故选：C
5、设集合， ，则集合元素的个数为（ ）
A．2B．3C．4D．5
【答案】B
【详解】
当时，y＝1；
当时，y＝0；
当x＝3时，．
故集合B共有3个元素．
考点二： 集合与集合之间的关系
【典例例题】
例1、（2022·广东潮州·高三期末）已知集合，．若，则m等于（ ）
A．0B．0或1C．0或2D．1或2
【答案】C
【详解】因为，，且，
所以或.
故选：C.
例题2、（2022·四川·高三阶段练习）集合的一个真子集可以为（ ）
A．B．C．D．
【答案】C
【详解】
解：由，即，解得，
所以，所以的一个真子集可以为．
故选：C
例题3．（2022·全国·高三专题练习）设集合，则集合A的子集个数为（ ）
A．16B．32C．15D．31
【答案】B
【详解】
因为集合，
所以集合A的子集个数为，
故选：B
【方法技巧与总结】
1.注意子集和真子集的联系与区别.
2.判断集合之间关系的两大技巧：
（1）定义法进行判断
（2）数形结合法进行判断：数轴、韦恩图
【变式训练】
1、设集合，，若，则实数的取值范围是（ ）．
A．B．
C．D．
【答案】D
【详解】
或，
因为，故可得，即实数的取值范围是.
故选：D.
2、已知集合，，，则实数的取值集合为（ ）
A．B．C．D．
【答案】C
【详解】
由题意得，，∵，，
∴实数a的取值集合为,
故选:C.
3、(多选)已知集合，，则下列命题中正确的是（ ）
A．若，则B．若，则
C．若，则或D．若时，则或
【答案】ABC
【详解】
，若，则，且，故A正确.
时，，故D不正确.
若，则且，解得，故B正确.
当时，，解得或，故C正确.
故选：ABC．
考点三： 集合的运算：交集、并集、补集运算
【典例例题】
例1．（2022·广东·金山中学高三期末）已知集合，集合，则（ ）
A．B．C．D．
【答案】C
【详解】集合，
集合，
故选：C
例2.（2022·全国·高三专题练习（理））已知集合，，则（ ）
A．B．
C．D．
【答案】D
【详解】
因为，，所以.
故选：D.
例3．（2022·广东·铁一中学高三期末）设集合，则（ ）
A．B．C．D．
【答案】B
【详解】由得，则集合，
由得，则集合，
所以.
故选：B.
【方法技巧与总结】
1.会用数形结合求集合的交集与并集运算
2.全集和补集是不可分离的两个概念
【变式训练】
1．（2022·广东中山·高三期末）设全集与集合的关系如图所示，则图中阴影部分所表示的集合是（ ）
A．B．C．D．
【答案】D
【详解】解：由图，元素属于但不属于，
即阴影部分对应的集合为，
故选：D．
2.已知集合，若，则实数的取值范围是（ ）
A．B．
C．D．
【答案】C
【详解】
由题意，，
当时，，即，符合题意；当，即时，，则有或，即
综上，实数的取值范围为.
故选：C.
3.已知集合，全集，则（ ）
A．B．C．D．
【答案】C
【详解】
解：由，即，等价于，解得或，
所以或，由，解得，
所以，
所以，所以；
故选：C
4．设集合、均为的子集，如图，表示区域（ ）
A．ⅠB．II
C．IIID．IV
【答案】B
由题意可知，表示区域II.
故选：B.
5．建党百年之际，影片《》《长津湖》《革命者》都已陆续上映，截止年月底，《长津湖》票房收人已超亿元，某市文化调查机构，在至少观看了这三部影片中的其中一部影片的市民中随机抽取了人进行调查，得知其中观看了《》的有人，观看了《长津湖》的有人，观看了《革命者》的有人，数据如图，则图中___________；___________；___________.
【答案】
由题意得：，解得：.
故答案为：；；.
【巩固练习】
一、单选题
1．已知全集，则（ ）
A．B．C．D．
【答案】B
【详解】
由题意知：，.
故选：B.
2．已知集合，集合，则（ ）
A．B．
C．D．
【答案】A
【详解】
由得：，即；
由，得：，即，，
.
故选：A.
3．已知集合，，，则（ ）
A．B．C．D．
【答案】A
【详解】
由题意得，，又则，
因为，所以，
故选：A.
4．若全集，集合，则图中阴影部分表示的集合为（ ）
A．B．C．D．
【答案】A
【详解】
由题图，阴影部分为，而，，
所以.
故选：A
5．已知集合，，则的子集个数为（ ）
A．4B．6C．8D．9
【答案】C
【详解】
因为，，
所以，因此中有三个元素，
所以的子集个数为，
故选：C
6．已知全集，集合，，则图中阴影部分表示的集合为（ ）
A．B．C．D．
【答案】B
【详解】
依题意，，则，而，
而图中阴影部分对应的集合为，于是得，
所以阴影部分表示的集合为.
故选：B
7．已知集合，，若，则实数a的取值范围是（ ）
A．B．C．D．
【答案】D
【详解】
解：由题知，
因为，
所以，当时，，解得，
当时，或，解得，
综上，实数a的取值范围是.
故选：D
8．设集合，，若，则实数a的取值范围是（ ）．
A．B．
C．D．
【答案】D
【详解】
或.
因为集合，，所以.
故选：D
二、多选题
9．已知集合，满足，，全集，则下列说法中可能正确的有（ ）
A．没有最大元素，有一个最小元素B．有一个最大元素，没有最小元素
C．有一个最大元素，有一个最小元素D．没有最大元素，也没有最小元素
【答案】ABD
【详解】
对于选项A：若，，，，则没有最大元素，有一个最小元素，故A可能成立；
对于选项B：若，，A有一个最大元素，B没有最小元素，故B可能成立；
对于选项C： A有一个最大元素，B有一个最小元素不可能，因为这样就有一个有理数不存在A和B两个集合中，与A和B的并集是所有的有理数矛盾；故C不可能成立.
对于选项D：若，，则A没有最大元素，B也没有最小元素，故D可能成立；
故选：ABD.
10．设表示不大于的最大整数，已知集合，，则（ ）
A．B．
C．D．
【答案】ABD
【详解】
对于A，，，，A正确；
对于C，，，C错误；
对于BD，，，
，，BD正确.
故选：ABD.表示
关系
文字语言
记法
基本关系
子集
集合的元素都是集合的元素
或
真子集
集合是集合的子集，但集合中至少 有一个元素不属于
或
相等
集合，的元素完全相同
空集
不含 任何元素的集合．空集是任何集合的子集
集合的并集
集合的交集
集合的补集
符号表示
图形表示
意义
性质
,
,
,