【新高考】2023年高考数学二轮复习精讲精练学案——第15讲 平面向量(原卷版+解析版)
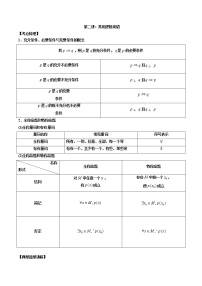
展开平面向量的两个定理
(1)向量共线定理:如果,则;反之,如果且,则一定存在唯一的实数,使.(口诀:数乘即得平行,平行必有数乘).
(2)平面向量基本定理:如果和是同一个平面内的两个不共线向量,那么对于该平面内的任一向量,都存在唯一的一对实数,使得,我们把不共线向量,叫做表示这一平面内所有向量的一组基底,记为,叫做向量关于基底的分解式.
2.平面向量的坐标运算
①已知点,,则,
②已知,,则,,
,.
,
3.平面向量线性运算的常用结论
(1)已知O为平面上任意一点,则A,B,C三点共线的充要条件是存在s,t,使得,且.
(2)在中,AD是BC边上的中线,则
【典型题型讲解】
考点一:平面向量的线性运算和数量积运算
【典例例题】
例1.(2022·广东珠海·高三期末)在中,,,,为边上的高;O为上靠近点A的三等分点,且,其中,,则( )
A.B.C.D.
例2.(2022·广东中山·高三期末)已知向量,的夹角为60°,,,则( )
A.2 B. C.D.12
【方法技巧与总结】
应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加法、减法或数乘运算,基本方法有两种:
(1)运用向量的线性运算法则对待求向量不断进行化简,直至用基底表示为止.
(2)将向量用含参数的基底表示,然后列方程或方程组,利用基底表示向量的唯一性求解.
(3)三点共线定理: A,B,P三点共线的充要条件是:存在实数,使,其中,O为AB外一点.
【变式训练】
1.(2022·广东潮州·高三期末)在的等腰直角中,为的中点,为的中点,,则( )
A.B.C.D.
2.(2022·广东汕尾·高三期末)对于非零向量,“”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
3.(2022·广东清远·高三期末)已知P是边长为4的正三角形所在平面内一点,且,则的最小值为( )
A.16B.12C.5D.4
4.(多选)(2022·广东深圳·高三期末)已知点O是边长为1的正方形ABCD的中心,则下列结论正确的为( )
A.B.
C.D.
5.(多选)(2021·广东汕头·高三期末)如图,平行四边形ABCD中,AB=2,AD=4,,E为CD的中点,AE与DB交于F,则( )
A.在方向上的投影为0B.
C.D.
6.(2022·广东·金山中学高三期末)已知向量与的夹角是,且,,若,则实数_______.
7.(2022·广东汕尾·高三期末)已知非零向量,且,则与的夹角为______.
8.(2022·广东广州·一模)已知菱形ABCD的边长为2,,点P在BC边上(包括端点),则的取值范围是___________.
【典型题型讲解】
考点二:平面向量的坐标运算
【典例例题】
例1.(2022·广东深圳·二模)已知点,向量,则向量( )
A.B.C.D.
例2.(2022·广东韶关·一模)已知向量,则下列说法正确的是( )
A.若,则向量可以表示平面内任一向量 B.若,则
C.若,则 D.若,则与的夹角是锐角
例3.在正方形ABCD中,M是BC的中点.若,则的值为( )
A.B.C.D.2
【方法技巧与总结】
熟记平面向量的坐标运算公式,学会建立直角坐标系.
【变式训练】
1.(2021·广东佛山·一模)已知向量,,,则实数k的值为______.
2.(2022·广东湛江·一模)已知向量,,若,则________.
3.(2022·广东广东·一模)已知向量满足,与的夹角为,则________.
4.(2022·广东·普宁市华侨中学二模)已知向量,,那么等于( )
A.B.C.1D.0
5.(2022·广东茂名·二模)已知向量(t,2t),=(﹣t,1),若(﹣)⊥(+),则t=_____.
6.已知正方形的边长为是的中点,点满足,则___________;___________.
【巩固练习】
一、单选题
1.下列说法错误的是( )
A.零向量与任一向量都平行B.方向相反的两个向量一定共线
C.单位向量长度都相等D.,,均为非零向量,若,则
2.已知下列结论:①;②;③;④⑤若 ,则对任一非零向量有;⑥若,则与中至少有一个为 ;⑦若与是两个单位向量,则.则以上结论正确的是( )
A.①②③⑥⑦B.③④⑦C.②⑦D.②③④⑤
3.在边长为1的正方形ABCD中,若,,,则等于( )
A.0B.1C.2D.2
4.下面四个命题哪些是平面向量,共线的充要条件( )
A.存在一个实数,B.,两向量中至少有一个为零向量
C.,方向相同或相反D.存在不全为零的实数,,
5.已知向量,不共线,且向量与平行,则实数( )
A.B.C.D.
6.中,若,点E满足,直线CE与直线AB相交于点D,则CD的长( )
A.B.C.D.
7.在中,E,F分别为的中点,点D是线段(不含端点)内的任意一点,,则( )
A.B.C.D.
8.已知D,E为所在平面内的点,且,,若,则( )
A.-3B.3C.D.
二、多选题
9.已知向量不共线,且,其中,若三点共线,则角的值可以是( )
A.B.C.D.
10.如图,直角三角形ABC中,D,E是边AC上的两个三等分点,G是BE的中点,直线AG分别与BD, BC交于点F,H设,,则( )
A.B.C.D.
11.已知向量,将向量绕原点逆时针旋转90°得到向量,将向量绕原点顺时针旋转135°得到向量,则( )
A.B.
C.D.
三、填空题
12.给出下列命题:
①若同向,则有; ②与表示的意义相同;
③若不共线,则有;④恒成立;
⑤对任意两个向量,总有;
⑥若三向量满足,则此三向量围成一个三角形.
其中正确的命题是__________填序号
13.在三角形ABC中,点D在边BC上,若,,则______.
14.在平行四边形中,,E、F是边,上的点,,,若,则平行四边形的面积为_________.
【新高考】2023年高考数学二轮复习精讲精练学案——第26讲 圆锥曲线(原卷版+解析版): 这是一份【新高考】2023年高考数学二轮复习精讲精练学案——第26讲 圆锥曲线(原卷版+解析版),文件包含第二十六讲圆锥曲线解析版docx、第二十六讲圆锥曲线原卷版docx等2份学案配套教学资源,其中学案共61页, 欢迎下载使用。
【新高考】2023年高考数学二轮复习精讲精练学案——第23讲 计数原理(原卷版+解析版): 这是一份【新高考】2023年高考数学二轮复习精讲精练学案——第23讲 计数原理(原卷版+解析版),文件包含第二十三讲计数原理解析版docx、第二十三讲计数原理原卷版docx等2份学案配套教学资源,其中学案共29页, 欢迎下载使用。
【新高考】2023年高考数学二轮复习精讲精练学案——第20讲 直线与平面、平面与平面垂直(原卷版+解析版): 这是一份【新高考】2023年高考数学二轮复习精讲精练学案——第20讲 直线与平面、平面与平面垂直(原卷版+解析版),文件包含第二十讲直线与平面平面与平面垂直解析版docx、第二十讲直线与平面平面与平面垂直原卷版docx等2份学案配套教学资源,其中学案共39页, 欢迎下载使用。