湖北省武汉市东湖高新区2022-2023学年八年级上学期期末考试数学试题（线下期末）

这是一份湖北省武汉市东湖高新区2022-2023学年八年级上学期期末考试数学试题（线下期末），共9页。

A.6B.0C.11D.69
2.若分式意义，实数的取值范围是（ ）
A.B.C.D.
用科学记数法表示为（ ）
A.B.C.D.
4.下列运算正确的是（ ）
A.B.C.D.
5.如图，已知，那么添加下列一个条件后，仍无法判定的是（ ）
A.B.平分C.D.
6.计算结果为（ ）
A.B.C.D.
7.下列因式分解正确的是（ ）
A.B.
C.D.
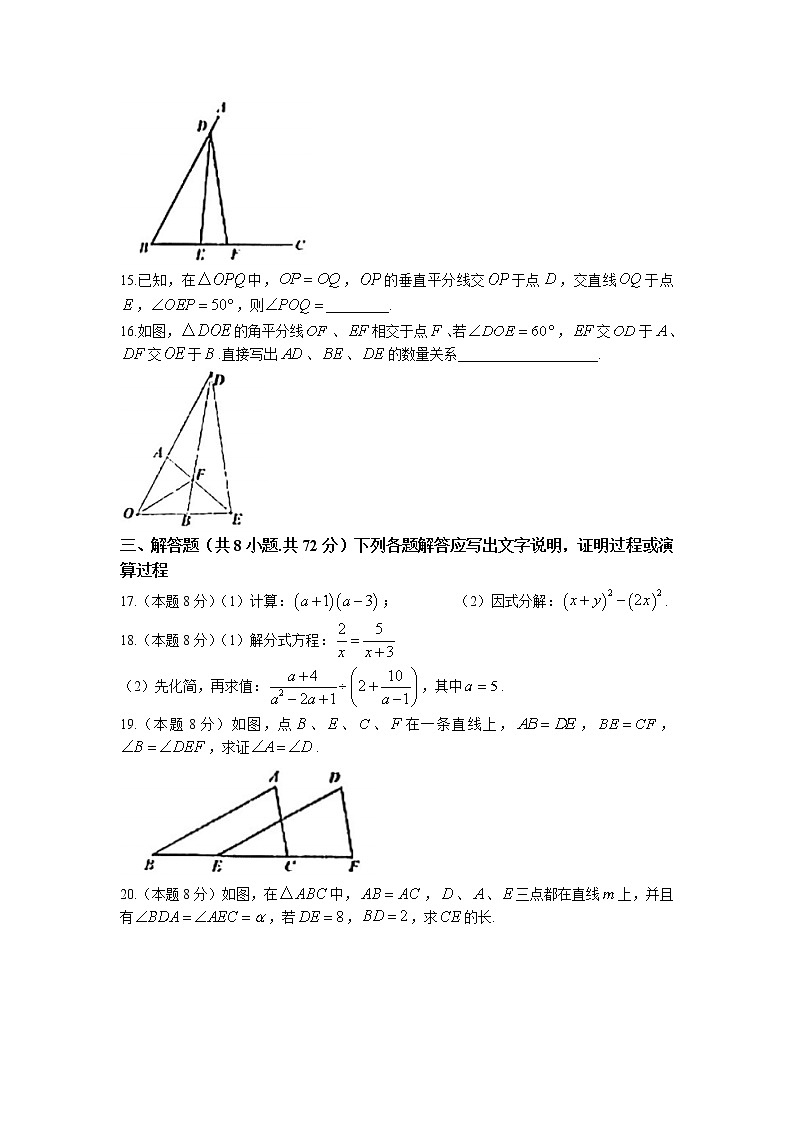
8.如图，已知，连接、，，则的度数为（ ）
A.25°B.30°C.35°D.65°
9.两个小组同时攀登一座480m高的山，第一组的攀登速度是第二组的1.5倍，第一组比第二组早0.5h到达顶峰，设第二组的攀登速度为m/min，则下列方程正确的是（ ）
A.B.C.D.
10.如图，在中，平分，下列说法：
①若，则；
②若，则；
③若，，，则；
④若，，，则.
其中正确的是（ ）
A.①②B.②③C.①③④D.②③④
二、填空题（共6小题，每小题3分，共18分）请将答案填在答题卡对应题号的位置上
11.若分式的值为0，则的值是__________.
12.若正边形的每个内角的度数为l40°.则的值是___________.
13.已知，则____________.
14.如图，已知，，，若，则__________.
15.已知，在中，，的垂直平分线交于点，交直线于点，，则_________.
16.如图，的角平分线、相交于点、若，交于、交于.直接写出、、的数量关系____________________.
三、解答题（共8小题.共72分）下列各题解答应写出文字说明，证明过程或演算过程
17.（本题8分）（1）计算：；（2）因式分解：.
18.（本题8分）（1）解分式方程：
（2）先化简，再求值：，其中.
19.（本题8分）如图，点、、、在一条直线上，，，，求证.
20.（本题8分）如图，在中，，、、三点都在直线上，并且有，若，，求的长.
21.（本题8分）如图是由小正方形组成的8×6网格，每个小正方形的顶点叫做格点.的三个顶点都是格点，为上一格点，点为上任一点.仅用无刻度的直尺在给定网格中完成画图，画图结果用实线表示，画图过程用虚线表示.
（1）在图1中，先将线段向右平移得到线段、画出线段，再在上画点，使；
（2）在图2中，先画出点关于的对称点、再在上找一点，使.
22.（本题10分）“以形释数”是利用数形结合思想证明代数问题的一种体现，做整式的乘法运算时利用几何直观的方法获取结论，在解决整式运算问题时经常运用.
例1：如图l，可得等式：；
例2：由图2，可得等式：.
（1）如图3，将几个面积不等的小正方形与小长方形拼成一个边长为的正方形，从中你发现的结论用等式表示为_____________________________；
（2）利用（1）中所得到的结论，解决下面的问题：已知，.求的值.
（3）如图4，拼成为大长方形，记长方形的面积与长方形的面积差为.设，若的值与无关，求与之间的数量关系.
23.（本题10分）【问题提出】如图1，在中，，是延长线上的点.连，以为边作（、在同侧），使、，连.若，判断与的位置关系，并说明理由.
【问题探究】
（1）先将问题特殊化.如图2，当在线段上，时，直接写出的度数__________；
（2）再探究具体情形、如图1，判断与的位置关系，并说明理由.
【问题拓展】
如图3，在中，.点为外一点，于，，，.则的长为____________.
24.（本题12分）在平面直角坐标系中，点为坐标原点，，，且，满足.
（1）求点、点的坐标.
（2）为轴上一动点，连接，过点在线段上方作，且.
①如图1，若点在轴正半轴上，点在第一象限，连接，过点作的平行线交轴于点，求点的坐标（用含的式子表示）.
②如图2，连接，探究当取最小值时，线段与的关系.
2022-2023学年度八年级上学期期末数学考试参考答案
一、选择题（每小题3分，共30分）
二、填空题（每小题3分，共18分）（填空题每小题赋一个分数）
三、解答下列各题（共8小题，共72分）
17.（共2小题，每小题4分，共8分）解：（1）
（2）
18.（本题8分）（1）
解：方程两边乘，得解得
经检验，
所以，原分式方程的解为
（2）
当时，原式
19.解：∵∴即
在与中
∴∴
20.解：∵∴，
∴，在与中
∴∴，
∵∴.∴.
21.解：第（1）、（2）问答案见左图；第（3）、（4）问答案见右图.备注：每小问正确得2分，合计8分
22.（本题10分）解：（1）∵正方形面积为，小块四边形面积总和为
∴由面积相等可得：，
故可得结论：；
（2）由（1）可知，
∵，；
∴，
∴；
（3）由题意知，，，，，
∵，∴，
即，
又∵为定值，∴，即.
23.（本题10分）解：（1）的度数为60°；
（2）方法一：过作，交的延长线于，连接，延长至使得.
如图所示：则，
∵，，
∴，即，
∵，，∴为等腰直角三角形，
∴∴为等腰直角三角形，
∴，，
∴∴，
又∵∴
∴∴
∴
∴为等腰直角三角形，
∴∴∴∴
方法二：过作，交的延长线于，如图所示：则，
∵，，∴为等腰直角三角形，
∴，∴，∴为等腰直角三角形，
∴，，∵，，∴为等腰直角三角形，
∴，∴，即，
在和中，
∴，∴，
∵，∴∴
（3）过作，交的延长线于，如图所示：则，
∵，∴，∵，∴，
在和中，
∴，∴，，
在和中，∴，
∴，∴，∴.
24.（本题12分）解：（1）∵，满足，，
∴，解得，∴，；
（2）①∴
∴，∴，
又∵，∴，∴，
而，∴，
∴在和中，，∴，∴；
∵且点在轴正半轴上，∴
②如图3，过点作轴于，
则可判定∴，∴，，
又∵，∴，∴，
∴是等腰直角三角形，∴，
∴点在过点且与轴正半轴成45°夹角的直线上运动，
如图4，设直线与轴交于点，当时，最小
∵，∴是等腰直角三角形，
∴是等腰直角三角形，且，
又∵，∴、均是等腰直角三角形，
∴，
∴且；1
2
3
4
5
6
7
8
9
10
B
D
A
A
C
B
C
C
D
D
题号
11
12
13
14
15
16
答案
1
9
11
5
65°或115°
备注
对一个给1分，对二个给3分，错误结果不扣分