




初中数学冀教版九年级下册30.4 二次函数的应用精品课件ppt
展开1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.(重点)2.利用二次函数解决拱桥及运动中的有关问题.(重、难点)
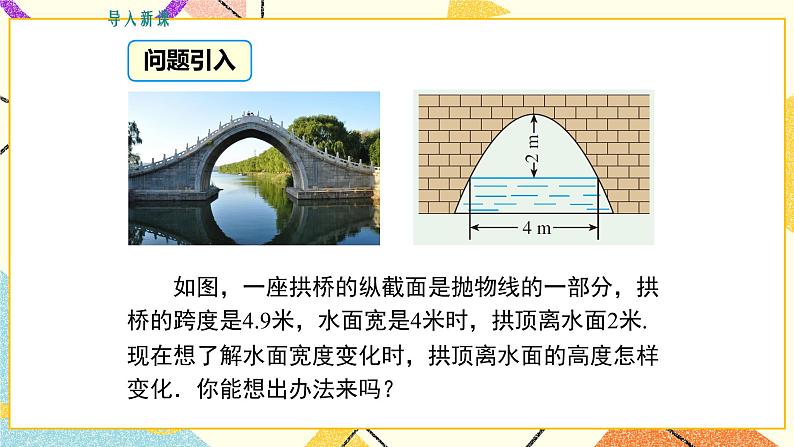
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
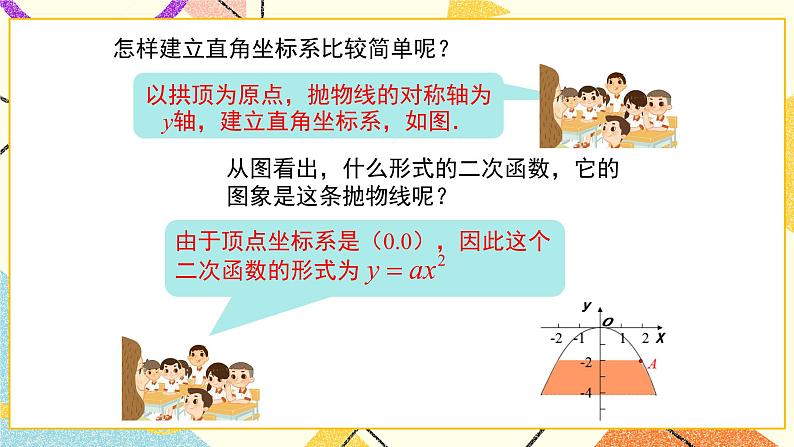
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
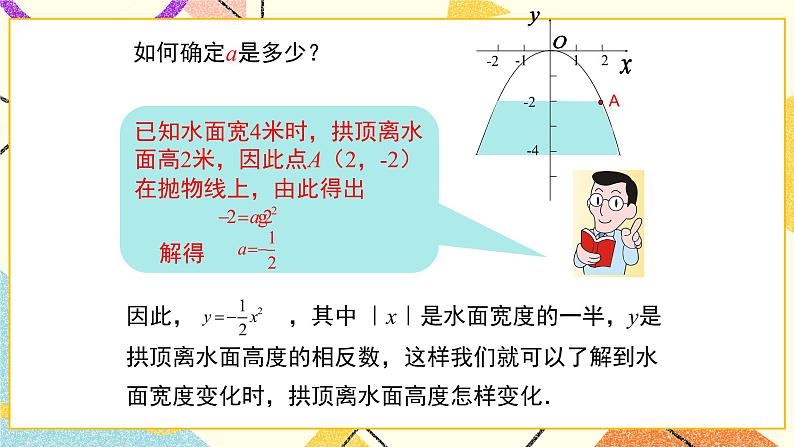
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时 从而因此拱顶离水面高1.125m
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
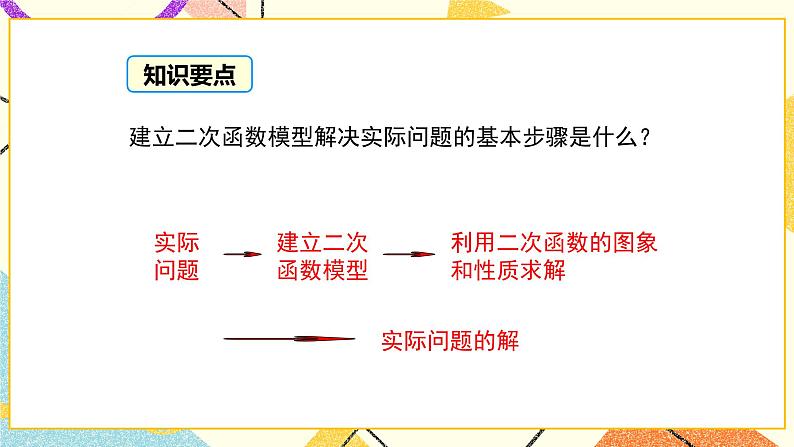
建立二次函数模型解决实际问题的基本步骤是什么?
利用二次函数的图象和性质求解
例1 某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
解:建立如图所示的坐标系,根据题意得,A点坐标为(0,1.25),顶点B坐标为(1,2.25).
根据对称性,如果不计其它因素,那么水池的半径至少要2.5m,才能使喷出的水流不致落到池外.
当y=0时,可求得点C的坐标为(2.5,0) ;同理,点 D的坐标为(-2.5,0) .
设抛物线为y=a(x+h)2+k,由待定系数法可求得抛物线表达式为:y=- (x-1)2+2.25.
例2:如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:如图,建立直角坐标系.则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).以点C表示运动员投篮球的出手处.
设以y轴为对称轴的抛物线的解析式为 y=a(x-0)2+k ,即y=ax2+k.而点A,B在这条抛物线上,所以有
所以该抛物线的表达式为y=-0.2x2+3.5.当 x=-2.5时,y=2.25 .故该运动员出手时的高度为2.25m.
问题1 图中是抛物线形拱桥,当拱顶离水面 2m时,水面宽 4m . 水面下降 1m,水面宽度增加多少?
(1)求宽度增加多少需要什么数据?
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求这组数据?需要先求什么?
(4)图中还知道什么?
(5)怎样求抛物线对应的函数的解析式?
问题2 如何建立直角坐标系?
问题3 解决本题的关键是什么?
解:如图建立直角坐标系.
解:建立合适的直角坐标系.
有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
解:设该拱桥形成的抛物线的解析式为y=ax2.∵该抛物线过(10,-4),∴-4=100a,a=-0.04∴y=-0.04x2.
例3 如果要使运动员坐着船从圣火的拱形桥下面穿过入场,现已知拱形底座顶部离水面 2 m,水面宽 4 m,为了船能顺利通过,需要把水面下降 1 m,问此时水面宽度增加多少?
解:建立如图所示坐标系,
由抛物线经过点(2,-2),可得
如果要使运动员坐着船从圣火的拱形底座下穿过入场,现已知拱形底座顶部离水面 2 m,水面宽 4 m,为了船能顺利通过,需要把水面下降 1 m,问此时水面宽度增加多少?
请同学们分别求出对应的函数解析式.
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
2.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为 ,那么铅球运动过程中最高点离地面的距离为 米.
3.公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O点恰在水面中心,OA=1.25米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下.为使水流较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米.如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流落不到池外?
解:如图建立坐标系,设抛物线顶点 为B,水流落水与x轴交于C点. 由题意可知A( 0,1.25)、 B( 1,2.25 )、C(x0,0).
设抛物线为y=a(x-1)2+2.25 (a≠0),
点A坐标代入,得a= - 1;
当y= 0时, x1= - 0.5(舍去), x2=2.5
∴水池的半径至少要2.5米.
∴抛物线为y=-(x-1)2+2.25.
人教版九年级上册22.3 实际问题与二次函数图片ppt课件: 这是一份人教版九年级上册22.3 实际问题与二次函数图片ppt课件,共18页。
初中数学冀教版九年级下册30.1 二次函数一等奖ppt课件: 这是一份初中数学冀教版九年级下册30.1 二次函数一等奖ppt课件,文件包含304第2课时实际问题中二次函数的最值问题课件ppt、304第2课时实际问题中二次函数的最值问题教案doc等2份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
冀教版九年级下册30.4 二次函数的应用公开课ppt课件: 这是一份冀教版九年级下册30.4 二次函数的应用公开课ppt课件,文件包含河北教育版数学九年级下·304二次函数的应用第1课时教学课件pptx、3041抛物线形问题教案docx、3041抛物线形问题同步练习docx等3份课件配套教学资源,其中PPT共15页, 欢迎下载使用。













