【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题07 初中数学重要定理的证明及其应用（原卷版+解析版）

这是一份【中考二轮专题复习】2023年中考数学全国通用专题备考试卷——专题07 初中数学重要定理的证明及其应用（原卷版+解析版），文件包含专题07初中数学重要定理的证明及其应用解析版docx、专题07初中数学重要定理的证明及其应用原卷版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
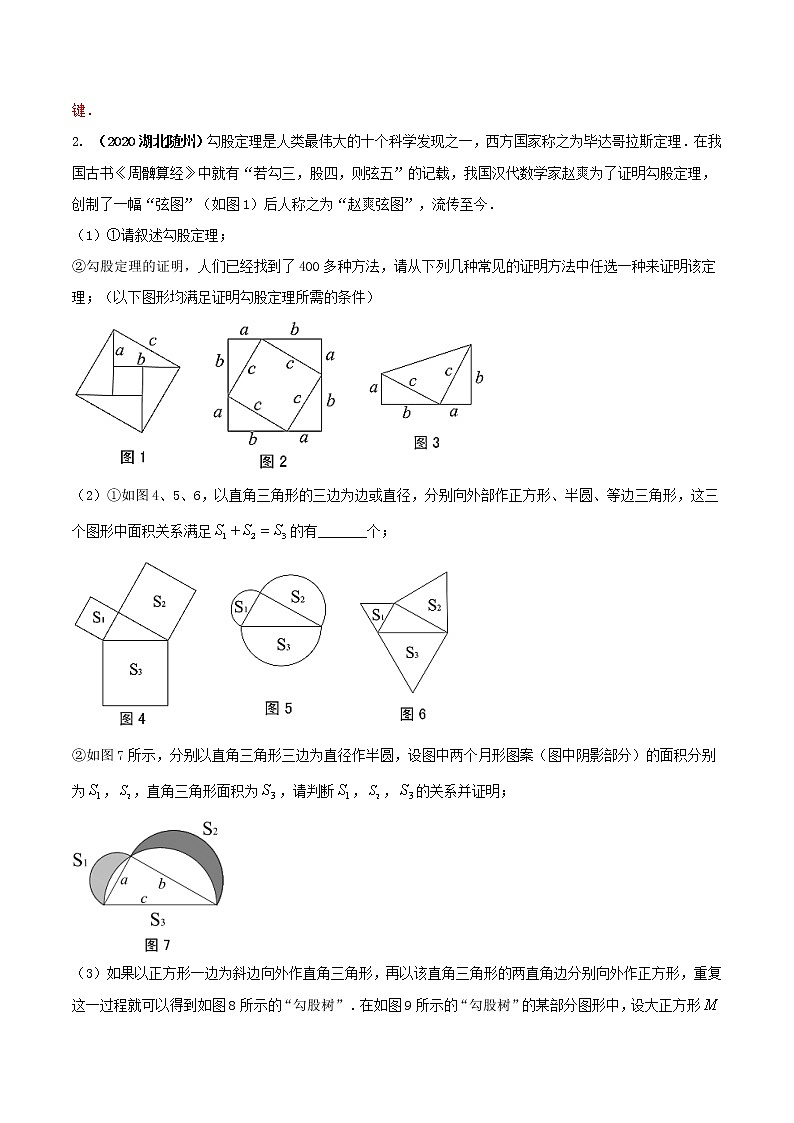
2023年中考数学二轮冲刺精准练新策略（全国通用）第五篇 中考数学冷门专题专题07 初中数学重要定理的证明及其应用1.（2022北京）下面是证明三角形内角和定理的两种添加辅助线的方法，选择其中一种，完成证明．三角形内角和定理：三角形三个内角和等于180°，已知：如图，,求证：方法一证明：如图，过点A作方法二证明：如图，过点C作 【答案】答案见解析【解析】选择方法一，过点作，依据平行线的性质，即可得到，，再根据平角的定义，即可得到三角形的内角和为．证明：过点作，则，． 两直线平行，内错角相等）点，，在同一条直线上，．（平角的定义）． 即三角形的内角和为．【点睛】本题主要考查了平行线的性质以及三角形内角和定理的运用，熟练掌握平行线的性质是解题的关键．2. （2020湖北随州）勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图1）后人称之为“赵爽弦图”，流传至今．（1）①请叙述勾股定理；②勾股定理的证明，人们已经找到了400多种方法，请从下列几种常见的证明方法中任选一种来证明该定理；（以下图形均满足证明勾股定理所需的条件）        （2）①如图4、5、6，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足的有_______个；        ②如图7所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案（图中阴影部分）的面积分别为，，直角三角形面积为，请判断，，的关系并证明；（3）如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图8所示的“勾股树”．在如图9所示的“勾股树”的某部分图形中，设大正方形的边长为定值，四个小正方形，，，的边长分别为，，，，已知，则当变化时，回答下列问题：（结果可用含的式子表示）①_______；②与的关系为_______，与的关系为_______．    【答案】（1）①如果直角三角形的两条直角边分别为，斜边为c，那么，（或者：在直角三角形中，两条直角边的平方和等于斜边的平方．）；②证明见解析；（2）①3，②结论；（3）①，②， ．【解析】【分析】（1）①根据所学的知识，写出勾股定理的内容即可；②根据题意，利用面积相等的方法，即可证明勾股定理成立；（2）①根据题意，设直角三角形的三边分别为a、b、c，利用面积相等的方法，分别求出面积的关系，即可得到答案；②利用三角形的面积加上两个小半圆的面积，然后减去大半圆的面积，即可得到答案；（3）①由（1）（2）中的结论，结合勾股定理的应用可知，；②由，则，同理可得，利用解直角三角形以及勾股定理，即可得到答案．【详解】（1）①如果直角三角形的两条直角边分别为，斜边为c，那么． （或者：在直角三角形中，两条直角边的平方和等于斜边的平方．）②证明： 在图1中，大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和．即，化简得．在图2中，大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和．即，化简得．在图3中，梯形的面积等于三个直角三角形的面积的和．即，化简． （2）①根据题意，则如下图所示：在图4中，直角三角形的边长分别为a、b、c，则由勾股定理，得，∴；在图5中，三个扇形的直径分别为a、b、c，则，，，∴，∵，∴，∴；在图6中，等边三角形的边长分别为a、b、c，则，，，∵，，∴，∴；∴满足的有3个，故答案为：3；②结论；，；（3）①如图9，正方形A、B、C、D、E、F、M中，对应的边长分别为a、b、c、d、e、f、m，则有由（1）（2）中的结论可知，面积的关系为：A+B=E，C+D=F，E+F=M，∴，，，∴故答案为：；②∵，∴，，由解直角三角形和正方形的性质，则，，∴；同理：；；；∴，∴，∵，∴．故答案为：；．【点睛】本题考查了求扇形的面积，解直角三角形，勾股定理的证明，以及正方形的性质，解题的关键是掌握勾股定理的应用，注意归纳推理等基础知识，考查运算求解能力、推理论证能力、归纳总结能力，是中档题．3.如图,等腰直角三角板如图放置,直角顶点C在直线m上,分别过点A,B作AE⊥直线m于点E,BD⊥直线m与点D.（1）求证:EC＝BD;（2）若设△AEC三边分别为a,b,c,利用此图证明勾股定理.证明：（1）∵△ABC是等腰直角三角形, ∴∠ACB＝90°,AC＝BC, ∴∠ACE+∠BCD＝90°,∵AE⊥EC, ∴∠EAC+∠ACE＝90°,∴∠BCD＝∠CAE,∵BD⊥CD, ∴∠AEC＝∠CDB＝90°,∴△AEC≌△CDB(AAS), ∴EC＝BD.（2）∵△AEC≌△CDB,△AEC三边分别为a，b，c,，∴BD＝EC＝a,CD＝AE＝b,BC＝AC＝c,∴S梯形＝(AE+BD)ED＝(a+b)(a+b),S梯形＝ab+c2+ab， ∴(a+b)(a+b)＝ab+c2+ab,整理可得a2+b2＝c2,故勾股定理得证.4．（2021广东省）我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，此公式与古希腊几何学家海伦提出的公式如出一辙，即三角形的三边长分别为，，，记，则其面积．这个公式也被称为海伦秦九韶公式．若，，则此三角形面积的最大值为（                             ）A．　　　　  B．    C．    D．【答案】C【解析】把，代入可得，因为，所以，而，所以，∴，把代入可得，当时，S最大，最大值为，考查秦九韶公式的变形处理技巧以及二次函数的配方5．（2021河北省）定理：三角形的一个外角等于与它不相邻的两个内角的和．已知：如图，∠ACD是△ABC的外角．求证：∠ACD＝∠A+∠B．证法1：如图，∵∠A+∠B+∠ACB＝180°（三角形内角和定理），又∵∠ACD+∠ACB＝180°（平角定义），∴∠ACD+∠ACB＝∠A+∠B+∠ACB（等量代换）．∴∠ACD＝∠A+∠B（等式性质）．证法2：如图，∵∠A＝76°，∠B＝59°，且∠ACD＝135°（量角器测量所得）又∵135°＝76°+59°（计算所得）∴∠ACD＝∠A+∠B（等量代换）．下列说法正确的是（　　）A．证法1还需证明其他形状的三角形，该定理的证明才完整 B．证法1用严谨的推理证明了该定理 C．证法2用特殊到一般法证明了该定理 D．证法2只要测量够一百个三角形进行验证，就能证明该定理【答案】B【解析】依据定理证明的一般步骤进行分析判断即可得出结论．∵证法1按照定理证明的一般步骤，从已知出发经过严谨的推理论证，得出结论的正确，具有一般性，无需再证明其他形状的三角形，∴A的说法不正确，不符合题意；∵证法1按照定理证明的一般步骤，从已知出发经过严谨的推理论证，得出结论的正确，∴B的说法正确，符合题意；∵定理的证明必须经过严谨的推理论证，不能用特殊情形来说明，∴C的说法不正确，不符合题意；∵定理的证明必须经过严谨的推理论证，与测量次解答数的多少无关，∴D的说法不正确，不符合题意；综上，B的说法正确．故选：B．6．（2021四川资阳）如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图，它是由四个全等的直角三角形和一个小正方形EFGH组成，恰好拼成一个大正方形ABCD．连结EG并延长交BC于点M．若AB＝，则GM的长为（　　）A． B． C． D．【答案】D【解析】由大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成，在直角三角形AEB中使用勾股定理可求出BF＝AE＝GC＝DH＝2，过点M作MN⊥FC于点N，由三角形EFG为等腰直角三角形可证得三角形GNM也为等腰直角三角形，设GN＝NM＝a，则NC＝GC﹣GN＝2﹣a，由tan∠FCB＝＝＝＝，可解得a＝．进而可得GM＝＝．解：由图可知∠AEB＝90°，EF＝1，∵大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成，故AE＝BF＝GC＝DH，设AE＝x，则在Rt△AEB中，有AB2＝AE4+BE2，即13＝x2+(2+x)2，解得：x＝2．过点M作MN⊥FC于点N，如图所示．∵四边形EFGH为正方形，EG为对角线，∴△EFG为等腰直角三角形，∴∠EGF＝∠NGM＝45°，故△GNM为等腰直角三角形．设GN＝NM＝a，则NC＝GC﹣GN＝5﹣a，∵tan∠FCB＝＝＝＝，解得：a＝．∴GM＝＝＝．故选：D．7．（2021四川泸州）在锐角△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，有以下结论：＝＝＝2R（其中R为△ABC的外接圆半径）成立．在△ABC中，若∠A＝75°，∠B＝45°，c＝4，则△ABC的外接圆面积为（　　）A． B． C．16π D．64π【答案】A【解析】已知c，所以求出∠C的度数即可使用题中的结论，得到关于R的方程，再求圆的面积即可．∵∠A+∠B+∠C＝180°，∴∠C＝180°﹣∠A﹣∠B＝180°﹣75°﹣45°＝60°，∵＝2R，∴2R＝＝＝，∴R＝，∴S＝πR2＝π（）2＝π．8.用1876年美国第十七任总统加菲尔德Garfield的方法证明勾股定理【答案】见解析。【解析】以a、b 为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于ab/2. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上. ∵ RtΔEAD ≌ RtΔCBE, ∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º. ∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形，它的面积等于c2又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD∥BC.∴ ABCD是一个直角梯形，它的面积等于S=（a+b）2……又因为这个直角梯形的面积等于三个小三角形面积之和，即S= 2×ab+c2……由得（a+b）2= 2×ab+c2化简：.从而结论得到证明。9. （2022山东济宁）知识再现：如图1，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c．∵，∴，∴（1）拓展探究：如图2，在锐角ABC中，∠A，∠B，∠C的对边分别为a，b，c．请探究，，之间的关系，并写出探究过程．（2）解决问题：如图3，为测量点A到河对岸点B的距离，选取与点A在河岸同一侧的点C，测得AC＝60m，∠A＝75°，∠C＝60°．请用拓展探究中的结论，求点A到点B的距离．【答案】（1），证明见解析    （2）米【解析】【分析】拓展研究：作CD⊥AB于点D，AE⊥BC于点E，根据正弦的定义得AE = csinB，AE= bsin∠BCA，CD= asinB，CD = bsin∠BAC，从而得出结论；解决问题：由拓展探究知， 代入计算即可．【小问1详解】（拓展探究）证明：作CD⊥AB于点D，AC⊥BC于点E．在RtΔABE中，，同理：，． ．．．．【小问2详解】（解答问题）解：在ΔABC中，∴解得：答：点A到点B的距离为m．【点睛】本题主要考查了解直角三角形，对于锐角三角形，利用正弦的定义，得出是解题的关键．